poj 1840：Eqs

最新推荐文章于 2018-08-12 09:05:01 发布

交错的0与1

最新推荐文章于 2018-08-12 09:05:01 发布

阅读量458

点赞数

分类专栏： hash表文章标签： poj hash表

本文链接：https://blog.csdn.net/u013898034/article/details/24159723

版权

hash表专栏收录该内容

1 篇文章 0 订阅

订阅专栏

给定a1，a2，a3，a4，a5，求满足方程的解的个数。其中xi<>0，i=1,2,3,4,5

首先要对方程做一个变形，如下

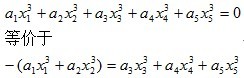
之后就暴力枚举x1、x2求得左式的值并计入一个hash表中，注意用hash表存左式的值的出现次数，而不是是否出现。原因在于当a1=a2时，x1=n，x2=m与x1=m，x2=n是两组解，此时左式的值相等，记为s，若右式=s，此时ans应加上hash[s]，而不是只加1。

之后再枚举x3、x4、x5的值求出右式的值比较该值在hash表中的数值，ans加上该数值。

对左式进行分析发现，极限情况下 -12,500,000 <= 左式的值 <= 12,500,000，故可以令MAXN=12,500,000，将hash表开成2*MAXN+5的char或short类型。注意用int可能会MLE。同时因为存在负数，所以将零点设为MAXN点。

因为刚接触hash，所以以上很大程度上参考了http://blog.csdn.net/lyy289065406/article/details/6647387这篇文章，同时借用了里面的图片。

代码：

#include <cstdio>
#include <iostream>
using namespace std;

const int MAXN=12500000;
char hash[2*MAXN+5]={0};
int ans=0;

int main(){
    int a1,a2,a3,a4,a5;
    cin>>a1>>a2>>a3>>a4>>a5;
    for(int i=-50;i<=50;i++){
        if(!i) continue;
        for(int j=-50;j<=50;j++){
            if(!j) continue;
            hash[(a1*i*i*i+a2*j*j*j)*(-1)+MAXN]++;
        }
    }
    for(int i=-50;i<=50;i++){
        if(!i) continue;
        for(int j=-50;j<=50;j++){
            if(!j) continue;
            for(int k=-50;k<=50;k++){
                if(!k) continue;
                if(a3*i*i*i+a4*j*j*j+a5*k*k*k<=MAXN &&
                   a3*i*i*i+a4*j*j*j+a5*k*k*k>=-MAXN)
                    ans+=hash[a3*i*i*i+a4*j*j*j+a5*k*k*k+MAXN];
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}