最短路径2----Acyclic算法

通用最短路径算法

distTo[s]初始化0，其余值初始化无穷大，放松G中的任意边，直到不存在有效边为止。此时distTo[w]即为从s到w的最短路径长度，且edgeTo[w]=e表示该最短路径的最后一条边为e。

Dijkstra算法----权重非负的加权有向图最短路径

从通用最短路径算法出发，distTo[s]初始化0，其余值初始化无穷大。不断将distTo[]中最小的非树顶点放松并加入树中，直到所有顶点都在树中，或者所有非树顶点值都为无穷大。

Dijkstra算法每次处理距离起始点距离最近的非树顶点，并且要求加权有向图的边权重非负。下面给出无环加权有向图最短路径一般解法。

无环加权有向图最短路径算法

distTo[s]初始化0，其余值初始化无穷大。按照拓扑排序顺序来放松所有顶点，可以在E+V正比时间内解决无环加权有向图最短路径。

无环加权有向图最短路径问题

顶点拓扑排序问题，利用顶点排序的逆后序。

利用dfs实现顶点排序

//有向图  dfs 顶点排序
//dfs搜索每个顶点会访问一遍   顶点的排序顺序
public class DepthFirstOrder {
	
	private boolean[] marked;
	//dfs过程中  顶点访问顺序
	private Queue<Integer> pre;
	//dfs过程中  某个顶点率先完成所有相邻顶点的访问顺序
	private Queue<Integer> post;
	//dfs过程中  某个顶点率先完成所有相邻顶点的逆序访问顺序
	private Stack<Integer> reversePost;
	
	public DepthFirstOrder(EdgeWeightedDigraph g){
		marked = new boolean[g.V()];
		pre = new LinkedList<>();
		post = new LinkedList<>();
		reversePost = new Stack<>();
		for(int v=0; v<g.V(); v++){
			if(!marked[v]){
				dfs(g, v);
			}	
		}
	}

	private void dfs(EdgeWeightedDigraph g, int v) {
		marked[v] = true;
		//访问该顶点则加入pre队列
		pre.add(v);
		for(DirectedEdge e : g.adj(v)){
			int w = e.to();
			if(!marked[w]){
				dfs(g, w);
			}
		}
		//顶点v所有相邻顶点都访问完毕则加入队列，由于递归其首先访问完成的在队列的最前面，最先输出
		post.add(v);
		//顶点v所有相邻顶点都访问完毕则加入栈  首先完成的在栈最下面，最后输出
		reversePost.push(v);
	}
	
	public Iterable<Integer> pre(){
		return this.pre;
	}
	
	public Iterable<Integer> post(){
		return this.post;
	}
	
	public Iterable<Integer> reversePost(){
		List<Integer> l = new ArrayList<>();
		while(!this.reversePost.isEmpty()){
			l.add(this.reversePost.pop());
		}
		return l;
	}
}

利用顶点排序实现拓扑排序

//拓扑排序  顶点排序逆后序实现方式
public class Topological {
	private Iterable<Integer> order;
	public Topological(EdgeWeightedDigraph g){
		DirectedCycle dc = new DirectedCycle(g);
		if(!dc.hasCycle()){
			DepthFirstOrder dfo = new DepthFirstOrder(g);
			this.order = dfo.reversePost();
		}
	}
	
	public Iterable<Integer> order(){
		return this.order;
	}
	
	public boolean isDAG(){
		return order != null;
	}
}

利用拓扑排序实现无环加权有向图最短路径

//无环加权有向图最短路径算法
public class AcyclicSP {
	
	private DirectedEdge[] edgeTo;
	private double[] distTo;
	
	public AcyclicSP(EdgeWeightedDigraph g, int s){
		edgeTo = new DirectedEdge[g.V()];
		distTo = new double[g.V()];
		for(int v=0; v<g.V(); v++){
			distTo[v] = Double.POSITIVE_INFINITY;
		}
		distTo[s] = 0.0;
		//按照拓扑排序顺序来松弛每个顶点可以得到最短路径
		Topological tp = new Topological(g);
		for(int v : tp.order()){
			relax(g, v);
		}
	}

	private void relax(EdgeWeightedDigraph g, int v) {
		for(DirectedEdge e : g.adj(v)){
			int w = e.to();
			if(distTo[w]>distTo[v]+e.weight()){
				distTo[w] = distTo[v]+e.weight();
				edgeTo[w] = e;
			}
		}
	}
	
	public double distTo(int v){
		return distTo[v];
	}
	
	public boolean hasPathTo(int v){
		return distTo[v]<Double.POSITIVE_INFINITY;
	}
	
	public Iterable<DirectedEdge> pathTo(int v){
		if(!hasPathTo(v)) return null;
		Stack<DirectedEdge> s = new Stack<>();
		for(DirectedEdge e=edgeTo[v]; e!=null; e=edgeTo[e.from()]){
			s.push(e);
		}
		List<DirectedEdge> ll = new ArrayList<>();
		while(!s.isEmpty()){
			ll.add(s.pop());
		}
		return ll;
	}

}

优先级限制下的并行任务调度

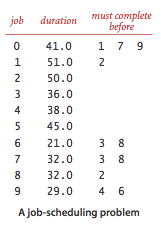
给定一系列任务，每个任务都需要一定的时间，并且某些任务必须在给定的任务之前完成。假定处理器数量是足够的，可以同时进行多个任务的执行，现给出最佳的任务调度方案。

                                                                                      

通过将并行任务调度问题进行转换，可以变为无环加权有向图的最长路径问题。其转换思想如下：

关键路径算法

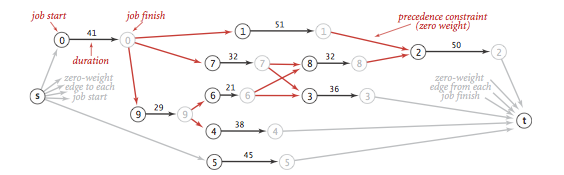
对于给定的任务创建一个无环加权有向图，包含起始点s，终点t，每个任务对应两个顶点起始和结束顶点；

对于每个任务，从任务起始点指向任务结束点有向边，权重为任务的执行时间；

对于每个优先级限制v-->w，添加一条由v结束顶点指向w开始顶点权重为0的有向边；

对于每个任务的起始顶点，添加一条由s指向每个任务起始顶点权重为0的有向边；

对于每个任务的结束顶点，添加一条由每个任务结束顶点指向结束顶点t的权重0的有向边；

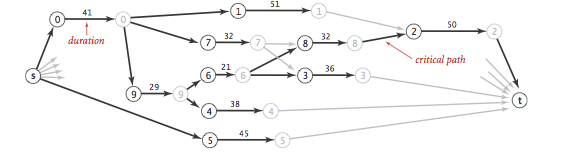
最佳方案的求解等价于从s到t的最长路径问题。

对于上述任务进行转换，得到如下所示：

                           

                           

无环加权有向图最长路径问题

通过改进顶点的松弛操作来实现，初始每个顶点初始为负无穷大，只有当发现新的较长路径时才更新distTo和edgeTo数组。

//无环加权有向图单点最长路径算法
public class AcyclicLP {
	
	private DirectedEdge[] edgeTo;
	private double[] distTo;
	
	public AcyclicLP(EdgeWeightedDigraph g, int s){
		edgeTo = new DirectedEdge[g.V()];
		distTo = new double[g.V()];
		for(int v=0; v<g.V(); v++){
			distTo[v] = Double.NEGATIVE_INFINITY;
		}
		distTo[s] = 0.0;
		
		Topological tp = new Topological(g); 
		for(int v : tp.order()){
			relax(g, v);
		}
	}

	private void relax(EdgeWeightedDigraph g, int v) {
		for(DirectedEdge e : g.adj(v)){
			int w = e.to();
			if(distTo[w]<distTo[v]+e.weight()){
				distTo[w] = distTo[v]+e.weight();
				edgeTo[w] = e;
			}
		}
	}
	
	public double distTo(int v){
		return distTo[v];
	}
	
	public boolean hasPathTo(int v){
		return distTo[v]<Double.POSITIVE_INFINITY;
	}
	
	public Iterable<DirectedEdge> pathTo(int v){
		if(!hasPathTo(v)) return null;
		Stack<DirectedEdge> s = new Stack<>();
		for(DirectedEdge e=edgeTo[v]; e!=null; e=edgeTo[e.from()]){
			s.push(e);
		}
		List<DirectedEdge> ll = new ArrayList<>();
		while(!s.isEmpty()){
			ll.add(s.pop());
		}
		return ll;
	}

}

优先级限制下并行任务调度关键路径算法

//优先级限制下的并行任务调度问题关键路径
public class CPM {
	
	public static void main(String[] args) {
		//任务数量
		int N = 10;
		//每个任务耗时
		double[] ww = new double[]{41,51,50,36,38,45,21,32,32,29};
		//优先级限制  prev[i]要先于next[i]完成
		int[] prev = new int[]{0,0,0,1,6,6,7,7,8,9,9};
		int[] next = new int[]{1,7,9,2,3,8,3,8,2,4,6};
		
		EdgeWeightedDigraph g = new EdgeWeightedDigraph(N*2+2);
		int s = 2*N;
		int t = 2*N+1;
		for(int i=0; i<N; i++){
			//每个任务的起始点和结束点作为一条边
			g.addEdge(new DirectedEdge(i, i+N, ww[i]));
			//起始点s到每个任务的起始点
			g.addEdge(new DirectedEdge(s, i, 0));
			//每个任务的结束点到结束点t
			g.addEdge(new DirectedEdge(i+N, t, 0));
		}
		//添加优先级限制
		for(int i=0; i<prev.length; i++){
			g.addEdge(new DirectedEdge(prev[i]+N, next[i], 0));
		}
		
		AcyclicLP alp = new AcyclicLP(g, s);
		for(int i=0; i<N; i++){
			System.out.println(alp.distTo(i));
		}
		System.out.println(alp.distTo(t));
	}

}

Dijsktra可以解决权重非负的加权有向图问题；Acyclic可以解决无环加权有向图问题。