堆与优先级队列

堆的定义

堆有最大堆以及最小堆之分，二叉堆结构类似于一颗完全二叉树，其中最大堆满足对于每一个节点其值大于左右孩子节点值。

可以用数组索引顺序按照完全二叉树的层序编号顺序来存储二叉堆，具体示意如下所示：

二叉树从1开始编号，分别对应数组索引从1位置处开始存储。对于k节点，其父节点为k/2,其左节点为2k,右节点为2k+1

                                                               

堆的调整算法

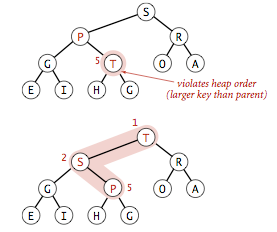
向上调整：以最大堆为例，如果某一个节点值小于其父节点，则需要交换该节点与父节点值，继续比较交换，直到根节点一直是有序的。

                                                                      

代码如下：

        private void swim(int k) {
		while(k>1 && less(k/2, k)){
			exch(k, k/2);
			k = k /2;
		}
	}

其中less是小于判断，exch为交换操作

        private void exch(int i, int j) {
		Key swap = pq[i];
		pq[i] = pq[j];
		pq[j] = swap;
	}

	private boolean less(int i, int j) {
		if(comparator==null){
			return ((Comparable<Key>)pq[i]).compareTo((Key)pq[j])<0;
		}else{
			return comparator.compare(pq[i], pq[j])<0;
		}
	}

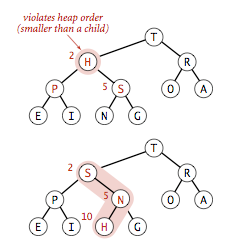
向下调整：最大堆，当某一个节点小于其左右孩子节点时，应该将该节点与左右孩子最大值节点交换，然后继续判断被交换孩子节点位置是否满足最大堆的定义。

                                                                           

代码如下：

        private void sink(int k) {
		while(2*k<=n){
			int j=2*k;
			if(j<n && less(j, j+1)) j++;
			if(!less(k, j)) break;
			exch(k, j);
			k = j;
		}	
	}

堆的建立过程

给定一个初始化数组来建立一个最大堆，假定数组长度为N,则从N/2到1位置处，对于每一个节点元素进行向下调整，则最终数组为一个最大堆。

        public MaxPQ(Key[] keys){
		n = keys.length;
		pq = (Key[]) new Object[n+1];
		for(int i=0; i<n; i++){
			pq[i+1] = keys[i];
		}
		for(int k=n/2; k>=1; k--){
			sink(k);
		}
	}

插入操作

首先判断当前元素数量与堆容量大小关系，判断是否需要扩容；如果不需要，则将新插入元素放置到数组最后位置。将最后位置元素执行向上调整操作，可以实现堆的平衡。

        public void insert(Key x){
		if(n==pq.length-1) resize(2*pq.length);
		pq[++n] = x;
		swim(n);
	}
        private void resize(int capacity) {
		Key[] tmp = (Key[]) new Object[capacity];
		for(int i=1; i<=n; i++){
			tmp[i] = pq[i];
		}
		pq = tmp;
	}

删除最大值

最大堆可以在O(1)内返回数组元素的最大值，在O(logN)内删除最大值并且调整堆有序。

删除最大值，即删除索引位置为1的元素，在此首先记录堆顶元素值，然后将数组最后一个元素与堆顶元素交换，对于堆顶新元素执行向下调整操作，以此保证堆有序。

        public Key delMax(){
		if(isEmpty()) return null;
		Key max = pq[1];
		exch(1, n--);
		sink(1);
		pq[n+1] = null;
		if(n>0 && n==(pq.length-1)/4)
			resize(pq.length/2);
		return max;
	}

最终用最大堆实现的优先级队列如下所示：

public class MaxPQ<Key> implements Iterable<Key>{
	
	private Key[] pq;
	private int n;
	private Comparator<Key> comparator;
	
	public MaxPQ(int initCapacity){
		pq = (Key[]) new Object[initCapacity+1];
		n = 0;
	}
	
	public MaxPQ(){
		this(1);
	}
	
	public MaxPQ(int initCapacity, Comparator<Key> comparator){
		this(initCapacity);
		this.comparator = comparator;
	}
	
	public MaxPQ(Comparator<Key> comparator){
		this(1, comparator);
	}
	
	public MaxPQ(Key[] keys){
		n = keys.length;
		pq = (Key[]) new Object[n+1];
		for(int i=0; i<n; i++){
			pq[i+1] = keys[i];
		}
		for(int k=n/2; k>=1; k--){
			sink(k);
		}
	}
	
	public void insert(Key x){
		if(n==pq.length-1) resize(2*pq.length);
		pq[++n] = x;
		swim(n);
	}
	
	public Key delMax(){
		if(isEmpty()) return null;
		Key max = pq[1];
		exch(1, n--);
		sink(1);
		pq[n+1] = null;
		if(n>0 && n==(pq.length-1)/4)
			resize(pq.length/2);
		return max;
	}
	
	 // is pq[1..N] a max heap?
    private boolean isMaxHeap() {
        return isMaxHeap(1);
    }

    // is subtree of pq[1..n] rooted at k a max heap?
    private boolean isMaxHeap(int k) {
        if (k > n) return true;
        int left = 2*k;
        int right = 2*k + 1;
        if (left  <= n && less(k, left))  return false;
        if (right <= n && less(k, right)) return false;
        return isMaxHeap(left) && isMaxHeap(right);
    }

	private boolean isEmpty() {
		return n == 0;
	}

	private void swim(int k) {
		while(k>1 && less(k/2, k)){
			exch(k, k/2);
			k = k /2;
		}
	}

	private void resize(int capacity) {
		Key[] tmp = (Key[]) new Object[capacity];
		for(int i=1; i<=n; i++){
			tmp[i] = pq[i];
		}
		pq = tmp;
	}

	private void sink(int k) {
		while(2*k<=n){
			int j=2*k;
			if(j<n && less(j, j+1)) j++;
			if(!less(k, j)) break;
			exch(k, j);
			k = j;
		}	
	}

	private void exch(int i, int j) {
		Key swap = pq[i];
		pq[i] = pq[j];
		pq[j] = swap;
	}

	private boolean less(int i, int j) {
		if(comparator==null){
			return ((Comparable<Key>)pq[i]).compareTo((Key)pq[j])<0;
		}else{
			return comparator.compare(pq[i], pq[j])<0;
		}
	}
	
	public int size() {
        return n;
    }
	
	@Override
	public Iterator<Key> iterator() {
		return new HeapIterator();
	}
	
	//迭代访问首先将原堆数据复制一份，然后执行迭代访问
	private class HeapIterator implements Iterator<Key> {

        // create a new pq
        private MaxPQ<Key> copy;

        // add all items to copy of heap
        // takes linear time since already in heap order so no keys move
        public HeapIterator() {
            if (comparator == null) copy = new MaxPQ<Key>(size());
            else                    copy = new MaxPQ<Key>(size(), comparator);
            for (int i = 1; i <= n; i++)
                copy.insert(pq[i]);
        }

        public boolean hasNext()  { return !copy.isEmpty();                     }
        public void remove()      { throw new UnsupportedOperationException();  }

        public Key next() {
            if (!hasNext()) throw new NoSuchElementException();
            return copy.delMax();
        }
    }

}

JDK中优先级队列PriorityQueue

核心变量：

    private static final int DEFAULT_INITIAL_CAPACITY = 11;

    /**
     * Priority queue represented as a balanced binary heap: the two
     * children of queue[n] are queue[2*n+1] and queue[2*(n+1)].  The
     * priority queue is ordered by comparator, or by the elements'
     * natural ordering, if comparator is null: For each node n in the
     * heap and each descendant d of n, n <= d.  The element with the
     * lowest value is in queue[0], assuming the queue is nonempty.
     */
    transient Object[] queue; // non-private to simplify nested class access

    /**
     * The number of elements in the priority queue.
     */
    private int size = 0;

    /**
     * The comparator, or null if priority queue uses elements'
     * natural ordering.
     */
    private final Comparator<? super E> comparator;

    /**
     * The number of times this priority queue has been
     * <i>structurally modified</i>.  See AbstractList for gory details.
     */
    transient int modCount = 0; // non-private to simplify nested class access

DEFAULT_INITIAL_CAPACITY为数组的默认初始化大小，size为已经存放元素数量，queue为数组。

优先级队列的构造函数   设置初始容量以及比较器，比较器用来决定最大堆以及最小堆

        public PriorityQueue(int initialCapacity,
                         Comparator<? super E> comparator) {
        // Note: This restriction of at least one is not actually needed,
        // but continues for 1.5 compatibility
        if (initialCapacity < 1)
            throw new IllegalArgumentException();
        this.queue = new Object[initialCapacity];
        this.comparator = comparator;
    }

基本调整算法

在k位置插入元素x,由于x插入会破坏堆序，因此需要对于k位置进行向下调整

/**
     * Inserts item x at position k, maintaining heap invariant by
     * demoting x down the tree repeatedly until it is less than or
     * equal to its children or is a leaf.
     *
     * @param k the position to fill
     * @param x the item to insert
     */
    private void siftDown(int k, E x) {
        if (comparator != null)
            siftDownUsingComparator(k, x);
        else
            siftDownComparable(k, x);
    }

具体的向下调整过程，k必定为非叶子节点，因此有k<size/2，获取k的左孩子2k+1(这里数组索引下标从0开始)，右孩子2k+2，然后求出左孩子与右孩子较大值，比较较大值与k位置处元素值，如果k位置处元素较小，则需要交换较小值与k位置处元素值，然后继续对于较小值进行向下调整。

@SuppressWarnings("unchecked")
    private void siftDownComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>)x;
        int half = size >>> 1;        // loop while a non-leaf
        while (k < half) {
            int child = (k << 1) + 1; // assume left child is least
            Object c = queue[child];
            int right = child + 1;
            if (right < size &&
                ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
                c = queue[child = right];
            if (key.compareTo((E) c) <= 0)
                break;
            queue[k] = c;
            k = child;
        }
        queue[k] = key;
    }

在k位置插入元素x，进行向上调整

 private void siftUp(int k, E x) {
        if (comparator != null)
            siftUpUsingComparator(k, x);
        else
            siftUpComparable(k, x);
    }

比较k与其父节点(k-1)/2大小关系，如果k位置处节点值大于其父节点，则将k与父节点交换，继续判断父节点与其父节点是否满足堆序。

@SuppressWarnings("unchecked")
    private void siftUpComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>) x;
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    }

堆的建立

private void heapify() {
        for (int i = (size >>> 1) - 1; i >= 0; i--)
            siftDown(i, (E) queue[i]);
    }

插入元素

public boolean offer(E e) {
        if (e == null)
            throw new NullPointerException();
        modCount++;
        int i = size;
        if (i >= queue.length)
            grow(i + 1);
        size = i + 1;
        if (i == 0)
            queue[0] = e;
        else
            siftUp(i, e);
        return true;
    }

删除堆顶元素

 @SuppressWarnings("unchecked")
    public E poll() {
        if (size == 0)
            return null;
        int s = --size;
        modCount++;
        E result = (E) queue[0];
        E x = (E) queue[s];
        queue[s] = null;
        if (s != 0)
            siftDown(0, x);
        return result;
    }

删除任意元素

public boolean remove(Object o) {
        int i = indexOf(o);
        if (i == -1)
            return false;
        else {
            removeAt(i);
            return true;
        }
    }

首先找到待删除元素的位置，遍历查找

private int indexOf(Object o) {
        if (o != null) {
            for (int i = 0; i < size; i++)
                if (o.equals(queue[i]))
                    return i;
        }
        return -1;
    }

然后将待删除元素删除

 private E removeAt(int i) {
        // assert i >= 0 && i < size;
        modCount++;
        int s = --size;
        if (s == i) // removed last element
            queue[i] = null;
        else {
            E moved = (E) queue[s];
            queue[s] = null;
            siftDown(i, moved);
            if (queue[i] == moved) {
                siftUp(i, moved);
                if (queue[i] != moved)
                    return moved;
            }
        }
        return null;
    }

可以用堆来实现优先级队列，利用堆可以实现堆排序，堆的调整操作时间复杂度均为O(logN)。

利用优先级队列可以每次取出集合的极值，不需要将所有元素都进行排序，可以在O(NlogK)时间内解决数组中前K个最大值问题。