Deep Residual Learning for Image Recognition 笔记

今天跑了把googlenet1应用到自己的分类任务中，识别率有大约有0.8%的提高。 看来大网络还是有用的， 只要你能很好的解决随着网络层数增多，容易引起过梯度消失或爆炸等问题。

https://github.com/ShaoqingRen/faster_rcnn/issues/47  这里有关于这个网络实现的讨论

https://github.com/beijbom/beijbom_python_lib/blob/master/beijbom_caffe_tools.py  这个是在caffe上的实现，可以参考一下。

https://github.com/KaimingHe/deep-residual-networks   这是caffe上的实现， 官方caffe已经实现该网络，只需要利用这里面的配置文件即可。

同时基于keras，torch等库，都有实现，可以进行尝试。

http://mp7.watson.ibm.com/ICCV2015/ObjectDetectionICCV2015.html ICCV 2015 Tutorial on Tools for Efficient Object Detection# 全部六位讲者的幻灯片已开放：1.导言,R.Feris 2.刚性模板,R.Benenson 3.区块法,J.Hosang 4.人工特征+CNN特征,XY.Wang 5. CNN法,KM.He 6.R-CNN,R.Girshick

http://research.microsoft.com/en-us/um/people/kahe/ilsvrc15/ilsvrc2015_deep_residual_learning_kaiminghe.pdf 何凯明对这个网络的PPT讲解。

下面转载于博客http://blog.csdn.net/cv_family_z/article/details/50328175 

这是微软方面的最新研究成果， 在第六届ImageNet年度图像识别测试中，微软研究院的计算机图像识别系统在几个类别的测试中获得第一名。

本文是解决超深度CNN网络训练问题，152层及尝试了1000层。

随着CNN网络的发展，尤其的VGG网络的提出，大家发现网络的层数是一个关键因素，貌似越深的网络效果越好。但是随着网络层数的增加，问题也随之而来。

首先一个问题是 vanishing/exploding gradients，即梯度的消失或发散。这就导致训练难以收敛。但是随着 normalized initialization [23, 9, 37, 13] and intermediate normalization layers[16]的提出，解决了这个问题。

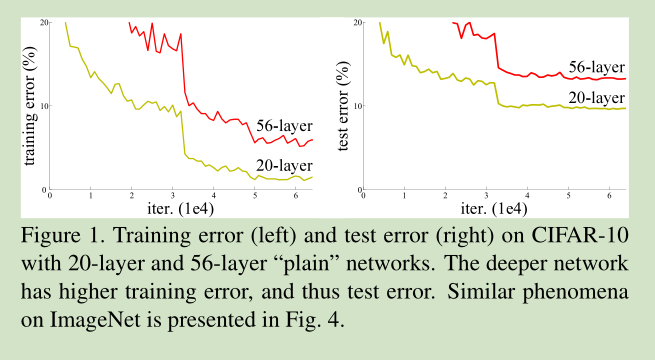
当收敛问题解决后，又一个问题暴露出来：随着网络深度的增加，系统精度得到饱和之后，迅速的下滑。让人意外的是这个性能下降不是过拟合导致的。如文献 [11, 42]指出，对一个合适深度的模型加入额外的层数导致训练误差变大。如下图所示： 

如果我们加入额外的 层只是一个 identity mapping，那么随着深度的增加，训练误差并没有随之增加。所以我们认为可能存在另一种构建方法，随着深度的增加，训练误差不会增加，只是我们没有找到该方法而已。

这里我们提出一个 deep residual learning 框架来解决这种因为深度增加而导致性能下降问题。 假设我们期望的网络层关系映射为 H(x), 我们让 the stacked nonlinear layers 拟合另一个映射， F(x):= H(x)-x , 那么原先的映射就是 F(x)+x。 这里我们假设优化残差映射F(x) 比优化原来的映射 H(x)容易。

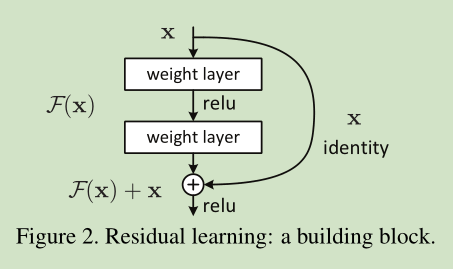
F(x)+x 可以通过shortcut connections 来实现，如下图所示：

2 Related Work 
Residual Representations 
以前关于残差表示的文献表明，问题的重新表示或预处理会简化问题的优化。 These methods suggest that a good reformulation or preconditioning can simplify the optimization

Shortcut Connections 
CNN网络以前对shortcut connections 也有所应用。

3 Deep Residual Learning 
3.1. Residual Learning 
这里我们首先求取残差映射 F(x):= H(x)-x，那么原先的映射就是 F(x)+x。尽管这两个映射应该都可以近似理论真值映射 the desired functions (as hypothesized)，但是它俩的学习难度是不一样的。

这种改写启发于 图1中性能退化问题违反直觉的现象。正如前言所说，如果增加的层数可以构建为一个 identity mappings，那么增加层数后的网络训练误差应该不会增加，与没增加之前相比较。性能退化问题暗示多个非线性网络层用于近似identity mappings 可能有困难。使用残差学习改写问题之后，如果identity mappings 是最优的，那么优化问题变得很简单，直接将多层非线性网络参数趋0。

实际中，identity mappings 不太可能是最优的，但是上述改写问题可能能帮助预处理问题。如果最优函数接近identity mappings，那么优化将会变得容易些。 实验证明该思路是对的。

3.2. Identity Mapping by Shortcuts 
图2为一个模块。A building block 
公式定义如下： 
 
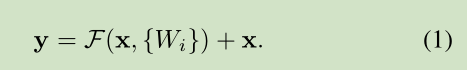
这里假定输入输出维数一致，如果不一样，可以通过 linear projection 转成一样的。

3.3. Network Architectures 
 

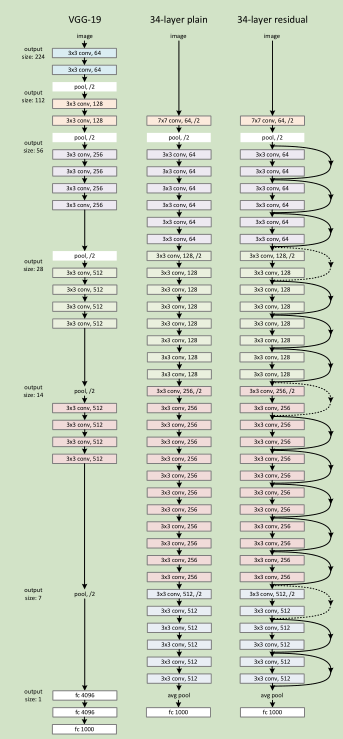
Plain Network 主要是受 VGG 网络启发，主要采用3*3滤波器，遵循两个设计原则：1）对于相同输出特征图尺寸，卷积层有相同个数的滤波器，2）如果特征图尺寸缩小一半，滤波器个数加倍以保持每个层的计算复杂度。通过步长为2的卷积来进行降采样。一共34个权重层。 
需要指出，我们这个网络与VGG相比，滤波器要少，复杂度要小。

Residual Network 主要是在 上述的 plain network上加入 shortcut connections

3.4. Implementation 
针对 ImageNet网络的实现，我们遵循【21,41】的实践，图像以较小的边缩放至[256,480]，这样便于 scale augmentation，然后从中随机裁出 224*224，采用【21,16】文献的方法。

4 Experiments 

下面是大神的笔记，直接转载到这里方便以后查看：

本文介绍一下2015 ImageNet中分类任务的冠军——MSRA何凯明团队的Residual Networks。实际上，MSRA是今年Imagenet的大赢家，不单在分类任务，MSRA还用residual networks赢了 ImageNet的detection, localization, 以及COCO数据集上的detection和segmentation, 那本文就简单分析下Residual Networks。

目录 
———————————— 
1. Motivation 
2. 网络结构 
3. 实验结果 
4. 重要reference

---

1. Motivation

作者首先抛出了这个问题， 深度神经网络是不是越深越好。 
照我们一般的经验，只要网络不训飞（也就是最早在LSTM中提出的vanishing/exploding problem），而且不过拟合， 那应该是越深越好。

但是有这么个情况，网络加深了， accuracy却下降了，称这种情况为degradation。如下图所示(详见[1])： 

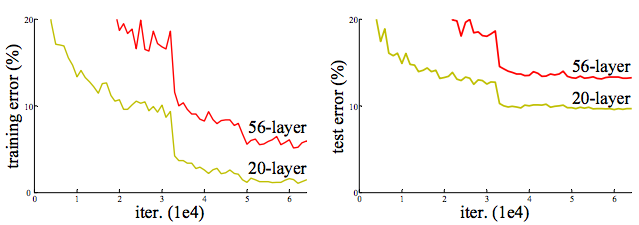
Cifar-10 上的training/testing error. 网络从20层加到56层，error却上升了。 

按理说我们有一个shallow net，在不过拟合的情况下再往深加几层怎么说也不会比shallow的结果差，所以degradation说明不是所有网络都那么容易优化，这篇文章的motivation就是通过“deep residual network“解决degradation问题。

2. 网络结构

Shortcut Connections

其实本文想法和Highway networks（Jurgen Schmidhuber的文章）非常相似， 就连要解决的问题（degradation）都一样。Highway networks一文借用LSTM中gate的概念，除了正常的非线性映射H（x, Wh）外，还设置了一条从x直接到y的通路，以T(x, Wt)作为gate来把握两者之间的权重，如下公式所示： 

y=H(x,WH)⋅T(x,WT)+x⋅(1−T(x,WT))  



shortcut原意指捷径，在这里就表示越层连接，就比如上面Highway networks里从x直接到y的连接。其实早在googleNet的inception层中就有这种表示： 

 

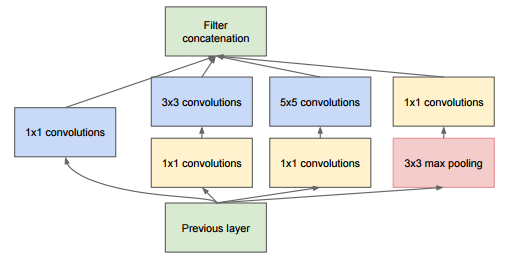
Residual Networks一文中，作者将Highway network中的含参加权连接变为固定加权连接，即 

y=H(x,WH)⋅WT+x  

Residual Learning

至此，我们一直没有提及residual networks中residual的含义。那这个“残差“指什么呢？我们想： 
如果能用几层网络去逼近一个复杂的非线性映射H(x)，那么同样可以用这几层网络去逼近它的residual function： F(x)=H(x)−x ，但我们“猜想“优化residual mapping要比直接优化H(x)简单。

推荐读者们还是看一下本文最后列出的这篇reference paper，本文中作者说与Highway network相比的优势在于：

x	Highway Network	Residual Network	评论
gate参数	有参数变量 WT	没参数，定死的, 方便和没有residual的网络比较	算不上优势，参数少又data-independent，结果肯定不会是最优的，文章实验部分也对比了效果，确实是带参数的error更小，但是 WT 这个变量与解决degradation问题无关
关门？	有可能关门( T(x,WT)=0 ）	不会关门	T(x,WT)∈[0,1] , 但一般不会为0

所以说这个比较还是比较牵强。。anyway，人家讲个故事也是不容易了。 

34层 residual network

网络构建思路：基本保持各层complexity不变，也就是哪层down－sampling了，就把filter数＊2， 网络太大，此处不贴了，大家看paper去吧， paper中画了一个34层全卷积网络， 没有了后面的几层fc，难怪说152层的网络比16-19层VGG的计算量还低。

这里再讲下文章中讲实现部分的 tricks：

1. 图片resize：短边长random.randint(256,480)
2. 裁剪：224＊224随机采样，含水平翻转
3. 减均值
4. 标准颜色扩充[2]
5. conv和activation间加batch normalization[3] 
   帮助解决vanishing/exploding问题
6. minibatch-size:256
7. learning-rate: 初始0.1, error平了lr就除以10
8. weight decay：0.0001
9. momentum：0.9
10. 没用dropout[3]

其实看下来都是挺常规的方法。

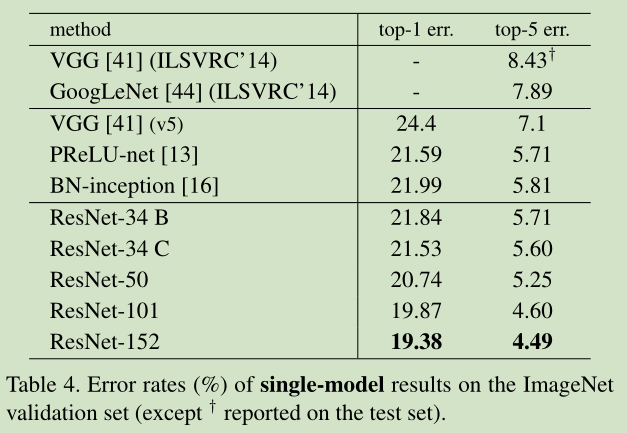
3. 实验结果

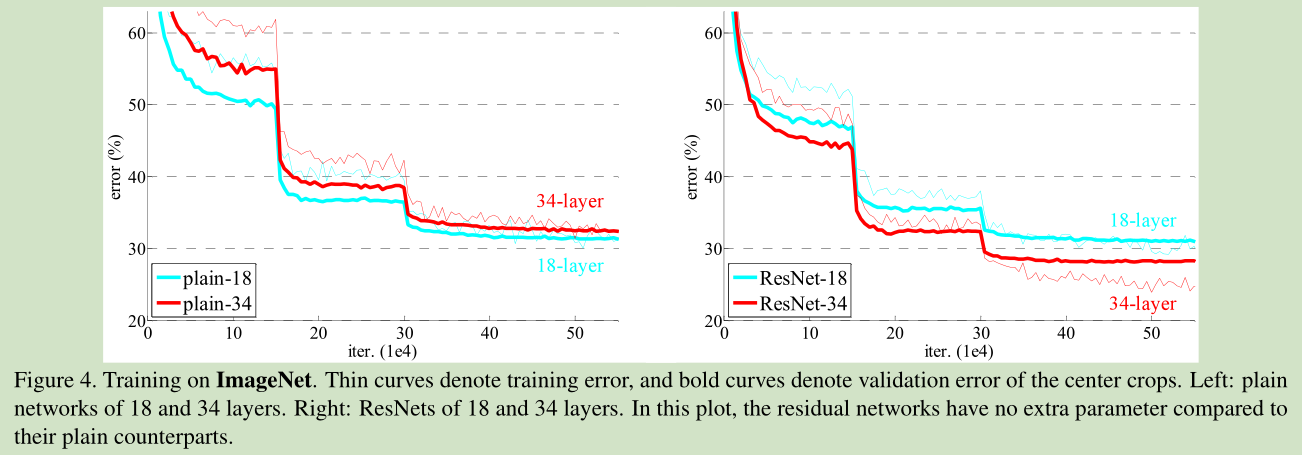
1. 34层与18层网络比较：训练过程中， 
   34层plain net（不带residual function）比18层plain net的error大 
   34层residual net（不带residual function）比18层residual net的error小，更比34层plain net小了3.5%(top1) 
   18层residual net比18层plain net收敛快

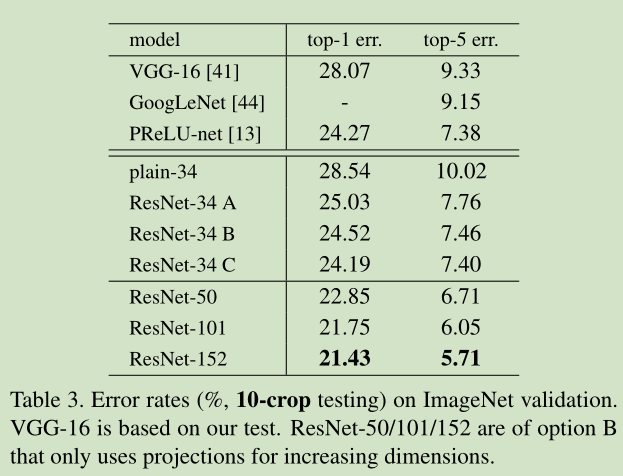
2. Residual function的设置： 
   A）在H(x)与x维度不同时， 用0充填补足 
   B） 在H(x)与x维度不同时， 带 WT  
   C）任何shortcut都带 WT  
   loss效果： A>B>C 
   
   
   

4. 重要reference

[1]. Highway Networks 
[2]. ImageNet Classification with Deep Convolutional Neural Networks 
[3]. Batch Normalization 
[4]. VGG