Geiger.A, Efficient large-scale stereo matching, In ACCV(2010)
摘要:本文提出的算法用于在双目立体视觉中进行快速高清晰度图像匹配。本算法通过在一组支持点上的三角测量构建视差的先验值。由于支持点可被精确地匹配,避免了使用其余点进行匹配造成的匹配模糊。进而可以通过有效利用视差搜索空间,重建精确的稠密视差图,而不必进行全局优化。另外,本算法可以自动决定视差范围,并易于并行运算。我们在大规模Middlebury试验平台上显示了该算法的高效性,并且很大程度上提高了当前性能。在一个单CPU核上计算一张1M像素图像的左右视差图大约耗时为1秒。
1. 引言
基于局部匹配的立体算法通常运算速度较快,但它的匹配结果与所选择的窗口大小有关,存在小窗口匹配率低,而大窗口产生边缘毛刺的矛盾。因此,纹理较少和平坦的表面难以获得准确的匹配。
基于全局匹配的算法通过在视差计算时引入平滑约束(采用归一化能量函数的形式),解决上述问题。因为基于MRF(Markov random field)能量函数的优化通常是难解的(NP-hard),人们提出许多近似算法,如图割(GC)算法和置信传播(BP)算法。然而这些算法对计算量和存储量的要求非常高。在这些算法中,需要提前获得视差范围,并且对正规化参数的选择非常关键。
本文提出一种用于立体匹配的生成概率模型,叫做ELAS(Efficient LArge-scale Stereo)算法。该算法通过降低匹配模糊,从而用小的聚集窗口实现稠密匹配。它通过在支持点上进行三角测量得到视差的先验值,由于该先验值是分片线性的,从而避免了无法处理无纹理和平坦表面的问题。
2.相关工作
局部算法在小窗口中对图像统计特性进行汇聚,相当于平滑操作。优化算法通常采取赢者通吃的策略,为每个像素选择的视差值在某种距离度量下具有最小值。然而,传统的局部算法有边缘毛刺缺陷,而且受到匹配模糊的影响。基于自适应支持窗的算法,通过调节窗口大小,或在一个固定大小的窗口内自适应调整像素权重,来提高边缘附近的匹配性能。但是,这种算法需要为每个像素计算许多权重系数,因此比固定窗口算法慢得多。
全局算法通过最小化MRF能量函数来进行显式的平滑。这个MRF能量函数可以分解为一个数据拟合项与一个正则项的和。因为对大多数能量函数的优化是难解的,人们提出了几种近似算法,如GC和BP算法。
半全局匹配算法,将多项式时间的1维扫描线算法推广为沿16个方向进行信息扩散。与传统的基于动态编程(DP)的算法相比,它虽然减少了条纹缺陷,提高了精度,但是计算复杂度随着计算路径的数目而增加。
本文提出的Bayesian立体匹配算法,能够实时地对高解析度图像计算出精确的视差图,而不需要进行全局优化。
3.ELAS匹配
虽然许多立体匹配是高度模糊的,但是其中某些可以被可靠地匹配。对于分片平滑的视差图,这些可靠的支撑点包含了有价值的先验信息,可用于估计视差图中其余的模糊部分。我们的方法是:采用全视差范围计算出稀疏的支撑点的视差,然后利用这些支撑点的图像坐标,通过Delaunay三角化来创建一个2D网孔(mesh)。利用先验信息消除匹配中的歧义,通过限制搜索区域来提高搜索的效率。这个先验信息采取的形式是计算一个由支撑点视差和三角网孔决定的分片线性函数。为了叙述简便,我们假设输入图像是校正过的,从而匹配点位于两张图片的同一条直线上。
3.1 支撑点
进行支撑点匹配,在一个正规化网格上,测量向量之间的l1距离是种有效的方法,这些向量是通过水平和垂直方向的Sobel 滤波器对9x9窗口的响应级联形成的。在我们的实验中,采用大小为3x3的Sobel算子,和一个固定步长为5像素的网格。视差搜索范围设为输入图像宽度的一半。
我们通过一致性检测来保证可靠性,即,在一条水平极线上进行从左向右和从右向左的扫描,只有得到相同匹配结果的点对,才予以保留。为避免错误匹配,删除与周围支撑点视差不一致的点。为了覆盖整幅图像,我们在图像角上增加了附加的支撑点,它们的视差值取自一个最近邻的像素。
3.2 立体匹配的生成模型
在我们的概率生成模型中,给定一个参考图像和一些支撑点,它可用于从其他图像中画出抽样。设 S = { s1, ...,sM }为一组可靠匹配的支撑点的集合,其中每个支撑点sm = ( um, vm, dm)T,由坐标和视差值定义。设 O = {o1, ...,oN } 为一组对该图像的观察,记on(l)和on(r)分别为观察到的左图像和右图像。规定左图为参考图像。
假定观察集{on(l), on(r)}和支撑点S是条件独立的,则联合分布为 p (dn , on(l), on(r) , S ) 分解为先验概率 p(dn | S, on(l)) 和图像似然率p(on(r) | on(l), dn) 的乘积,
p (dn , on(l), on(r) ,S ) ∝ p(dn | S, on(l)) p(on(r) |on(l), dn)
其中先验概率正比于一个Gaussian分布
其中均值 µ(S, on(l)) 可以表示为一个分片线性函数,用于在支撑点形成的Delaunay三角形上进行视差的线性内插。对于第 i 个三角形,有
µi (on(l)) = ai un + bi vn + ci
其中点(un,vn)属于这个三角形,对该点的观察记为on = (un, vn, fn)T。对于任意一个三角形,参数(ai ,bi ,ci)可通过求解一个线性方程组求得。
图像似然率可以表示为一个约束Laplace分布:
其中 fn(l)) 和fn(r)) 分别为左右图像的特征向量,β 为常数。在我们的实验中,特征向量 fn 是在点(un, vn)的5x5邻域内的图像导数的级联,由Sobel滤波器响应求得,是一个2x5x5=50维的向量。
已知支撑点集 S 和左图中的点on(l),计算它在右图中对应样点的步骤为:
1. 已知 S 和 on(l),由p(dn | S, on(l)) 得到深度 dn。
2. 已知on(l) 和 dn,由p(on(r) | on(l), dn)得到观察 on(r)。
3.3 视差估计
我们运用最大后验(MAP)估计来计算视差
dn* = argmax p(dn |on(l),o1(r), ... ,oN(r), S)
其中后验概率分解为
p(dn | on(l), o1(r), ... , oN(r), S) ∝ p(dn |S,on(l))p(o1(r), ... , oN(r) | on(l),dn)
其中在右图极线上的样点的联合分布可以简化为
最后得到能量函数
通过对其最小化即可求得稠密视差图。
4. 实验评估
5. 结论和展望
本文提出一种立体匹配的Bayesian方法,它能够实时计算高清晰度图像的精确视差图。本文显示,通过从可靠的支撑点估计先验分布可以减少立体匹配的不确定性。









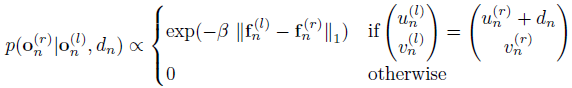
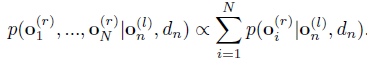















 1145
1145

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








