fft 窗函数特性对比

fft 窗函数特性

窗名称	主瓣宽度	旁瓣相对衰减（旁瓣抑制）	旁瓣能量占比	最大值（32个点时）	最小值（32个点时）
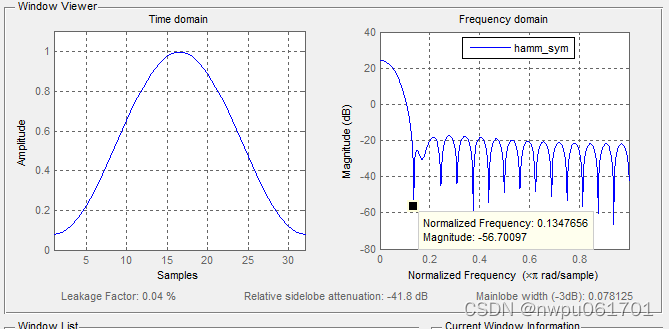
hamming(symmetric)	4.3125*谱线间隔	-41.8dB	0.04%	0.9976	0.0800
hamming(periodic)	4.0625*谱线间隔	-41.8dB	0.04%	1	0.0800
bartlett	4*谱线间隔	-26.5dB	0.28%	0.9677	0
bartlett_hanning	4.09*谱线间隔	-35.8dB	0.03%	0.9903	0
blackman(symmetric)	6.125*谱线间隔	-58.2dB	0%	0.9958	0
blackman(periodic)	6*谱线间隔	-58.1dB	0%	1	0
black-harris(symmetric)	8.31*谱线间隔	-92dB	0%	0.9941	6e-5
black-harris(periodic)	6*谱线间隔	-91.9dB	0%	1	6e-5
bohman	6.188*谱线间隔	-46dB	0%	0.9950	0
chebyshev(60dB旁瓣衰减）	5.0625*谱线间隔	-60dB（可设置）	0%	1	0.0189
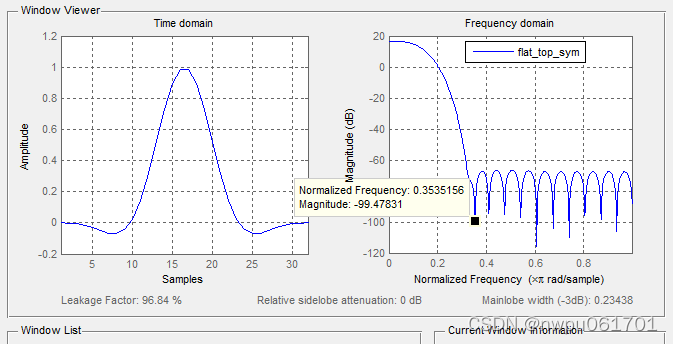
flat_top(symmetric)	11.3125*谱线间隔	0dB?	96.84%	0.9878	-0.0695
flat_top(periodic)	10*谱线间隔	0dB?	96.74%	1	-0.0705
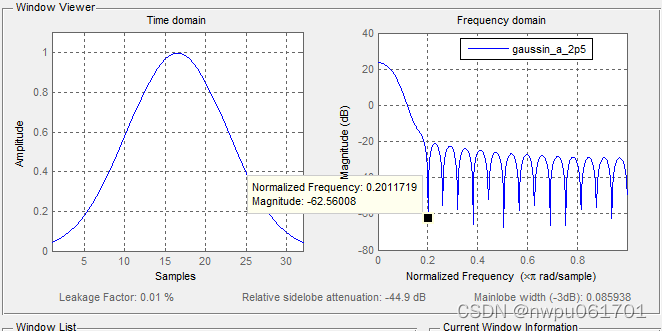
gaussin（a=2.5)	6.4375*谱线间隔	-44.9dB	0.01%	0.9968	0.0439
hann(symmetric)	4.125*谱线间隔	-31.5dB	0.05%	0.9974	0
hann(periodic)	4*谱线间隔	-31.5dB	0.05%	1	0
Kaiser(β=6）	4.4375*谱线间隔	-44.1dB	0%	0.9998	0.0149
nuttall(symmetric)	9.4375*谱线间隔	-88.8dB	0%	0.9942	3.628e-4
nuttall(periodic)	9*谱线间隔	-88.9dB	0%	1	3.628e-4
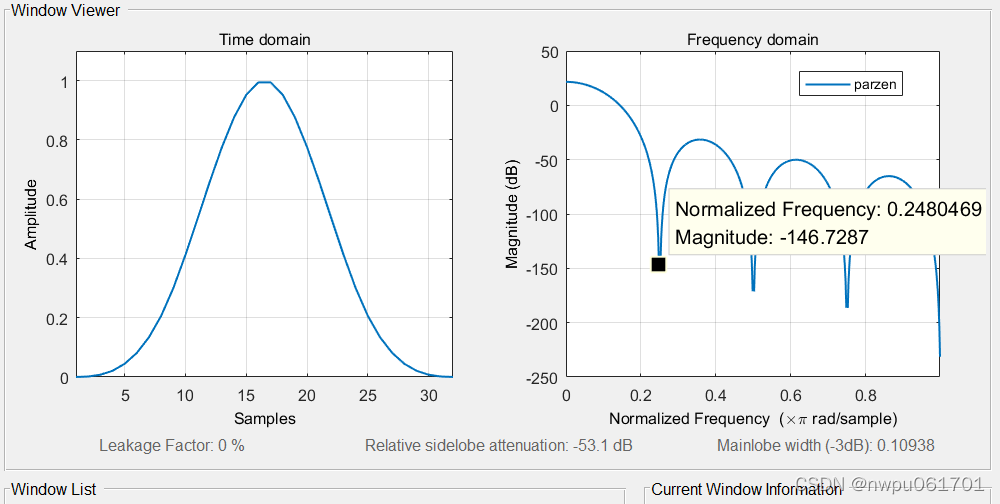
parzen	7.9375*谱线间隔	-53.1dB	0%	0.9943	6.1035e-5
rectangle	1.7500*谱线间隔	-13.2dB	9.12%	1	1
taylor(nb=4, sl=50)	4.1875*谱线间隔	-44.2dB	0.02%	1.8861	0.1341
triang	3.9375*谱线间隔	-26.6dB	0.27%	0.9688	0.0313
tukey（a=0.5）	2.75*谱线间隔	-15.1dB	3.57%	1	0

 

 

 

 

 

 

 

 

 

 

 

 

 

N = 128;
hamm = hamming(N);
barthann = barthannwin(N);
bartlet = bartlett(N);%旁瓣抑制-26.5dB
blackman_sym = blackman(N,'symmetric');
blackman_prd = blackman(N,'periodic');

blackman_harris_sym = blackmanharris(N,'symmetric');
blackman_harris_prd = blackmanharris(N,'periodic');
bohman_sym = bohman(N,'symmetric');
bohman_prd = bohman(N,'periodic');

chebyshev_60 = chebwin(N, 60);
flat_top_sym = flattopwin(N, 'symmetric');
flat_top_prd = flattopwin(N, 'periodic');
gauss = gausswin(N,2.5);

幅值恢复系数= 1/ Coherent Gain
能量恢复系数= 1/sqrt[Equivalent Noise Bandwidth x (Coherent Gain^2)]