从零开始学习SVM（二）---松弛变量

上一篇文章《从零开始学习SVM》中引出了想要进行分开两个样本需要的目标函数，但是是针对线性可分的。如下图所示，是存在一个超平面完完全全的分开两类样本。

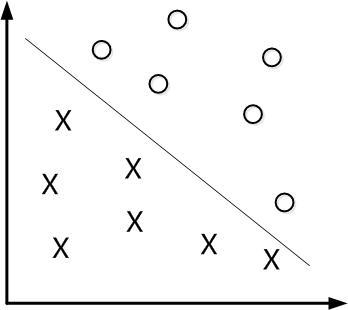
但是如果是线性不可分呢？同样以猫狗数据为例，有的狗被主人打扮确实像猫，人都容易混合，像这种相似性比较高的数据，可能无法通过线性的方法完全分开

即无法用一个超平面把两类数据分开，属于一种混合的状态，就如下图一样

一方面来说，人的识别准确度都无法达到100%，更别说机器了，一般只要机器能达到一个可以容忍的准确度，能完成分类工作就可以了。允许少部分样本在两个边界线内，甚至超出边界线（上图中的红点）。与此同时在最大化间隔的同时，不满足约束的样本应该尽可能的少。

$$min_w,_b \frac{1}{2} ||w||^2$$ $$s.t. y_i(w^Tx_i+b)\geqslant1，i=1,2,3\dots,m.$$
我们的优化目标可以写为：
$$min_w,_b \quad \frac{1}{2}||w||^2+C\sum_{i}^{m}\zeta_i$$ $$s.t.\quad y_i(w^T+b)\geqslant1- \zeta_i$$ $$\zeta_i\geqslant0,i=1,2,3\dots,m$$
引入”松弛变量”的概念，显然每个样本都有其对应的”松弛变量”，表征了该样本不满足约束的程度—来自《机器学习》周志华。我的理解是样本离虚线边界距离的大小，越小则不满足约束程度越小，越大则不满足约束程度越大。同理我们通过拉格朗日乘子法可得到的拉格朗日函数为：
$$L(w,b,\alpha,\zeta,u)= \frac{1}{2}||w||^2+C\sum_{i}^{m}\zeta_i+\sum_{i}^{m}\alpha_i(1-\zeta_i-y_i(w^T+b))-\sum_{i}^{m}u_i\zeta_i$$
对 $L(w,b,\alpha,\zeta,u)$的 $w,b,\zeta$求偏导为零可以得到
$$w=\sum_{i}^{m}\alpha_iy_ix_i$$ $$0=\sum_{i}^{m}\alpha_iy_i$$ $$C=\alpha_i+u_i$$
经过带入可以惊人的发现，”松弛变量”并没有在目标函数里面，感觉整个人都轻松了一把。跟之前的不带有”松弛变量”的目标函数的唯一区别是 $\alpha$的取值范围变化了
$$max_\alpha \quad\sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i=1}^{m}{\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j}$$
$$s.t. \quad \sum_{i=1}^{m}\alpha_iy_i=0$$ $$C\geqslant\alpha_i \geqslant0,i=1,2,\dots,m$$
KKT条件：
$$\alpha_i\geqslant0$$ $$y_if(x_i)-1+\zeta_i\geqslant0$$ $$\alpha_i(y_if(x_i)-1+\zeta_i)=0$$ $$\zeta_i\geqslant0,u_i\zeta_i=0$$
KKT条件基本上与不带有”松弛变量”的目标函数一致，求解方法也一样，最大的收获是我们有了得到一定准确度的分类器的方法，使得svm不仅仅应用到科研理论中，同样可以应用到生产，适用业界数据多样、噪声随机多样的情形，满足业界的需求。后面的学习我们将针对该目标函数进行优化，我们将继续对线性分类进行讨论，后面会继续推出非线性的分类解决方法