1. 1范数和2范数
L1和L2正则化,其实就是在损失函数后面加一个1范数或2范数约束。
1-范数:
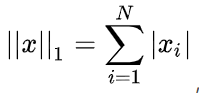 ,1范数表示向量元素绝对值之和。
,1范数表示向量元素绝对值之和。
2-范数:
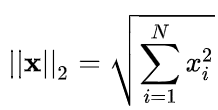 也称欧几里得范数。即向量元素绝对值的平方和再开方。
也称欧几里得范数。即向量元素绝对值的平方和再开方。
2. L1正则化
假设有如下带L1正则化的损失函数:
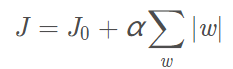
令![]() ,则 J = J0 + L
,则 J = J0 + L
其中J0为原来损失函数,J为加了L1正则项后的损失函数。α是正则化系数。注意到L1正则化是权值的绝对值之和,J是带有绝对值符号的函数,因此J是不完全可微的。机器学习的任务就是要通过一些方法(比如梯度下降)求出损失函数的最小值。当我们在原始损失函数J0 后添加L1正则化项时,相当于对J0做了一个约束。此时我们的任务变成在L约束下求出J0取最小值的解。
考虑二维(即两个变量:和
)的情况,即只有两个权值
和
。求解J0的过程可以画出等值线(下图彩色的圆),同时L1正则化的函数L也可以在
二维平面上(解空间)画出。
 其中,彩色的圈是J0 的等值线,最里面的是J0取得最小值时,
其中,彩色的圈是J0 的等值线,最里面的是J0取得最小值时,和
的取值位置。当然有人问,为什么J0是圆,这个链接有写,感兴趣可以看一看:https://blog.csdn.net/peter_mama/article/details/104208172。 而L1正则项在平面上的图形就是菱形。若没有正则项(即菱形),那么
和
可以在解空间里面 任意地取值:
有人问:为什么要搞个正则项,直接让和
任意地取值,取到J0 的最小处不就最好吗?
原因是:J0是表示模型对训练集的损失值,如果和
直接去到J0的最小处(假设为K点),则表示,模型对训练集过拟合。因此我们加入正则项的目的是,防止模型过拟合。正则项规定,
和
只能在菱形连取值。不能超过菱形。
因此,在图中,当菱形和等值线首次相交的地方(上图中的黑点),就是最优解。注意到这个顶点的值是,可以直观想象,因为LLL函数有很多『突出的角』(二维情况下四个,多维情况下更多),J0与这些角接触的机率会远大于与L其它部位接触的机率,而在这些角上,会有很多权值等于0,这就是为什么L1正则化可以产生稀疏模型,进而可以用于特征选择。
而正则化前面的系数α,可以控制L图形的大小。α越小,L的图形越大(上图中的菱形);α越大,L的图形就越小,可以小到黑色方框只超出原点范围一点点。
当α很小时,则以L1为例,上图的菱形区域将会覆盖 J0 的最小处(K点),则表示能取到K点,则正则化失效,模型仍会过拟合。当α很大时,菱形区域很小,容易造成过拟合。
从梯度角度说明为什么L1容易稀疏:
那梯度下降法来训练权重为例:
 切向量方向是当前运动方向,法向量是垂直切向量的。设最小点为左图红色点,只有当法向量方向与 当前点与最小值方向 重合,那么(w1,w2)点才停止运动,否则它还会沿着切向量方向运动,所以多数情况,对于L1来说,(w1,w2)点都是会运动到菱形的端点(0,w2)的,所以L1正则化,容易-产生稀疏的权重。
切向量方向是当前运动方向,法向量是垂直切向量的。设最小点为左图红色点,只有当法向量方向与 当前点与最小值方向 重合,那么(w1,w2)点才停止运动,否则它还会沿着切向量方向运动,所以多数情况,对于L1来说,(w1,w2)点都是会运动到菱形的端点(0,w2)的,所以L1正则化,容易-产生稀疏的权重。
总结L1:
1. L1正则化的特点是,优化时,会有很多权值等于0,使得特征矩阵稀疏化,进而可以用于特征选择。
2. 由于L1正则化容易产生权值稀疏,所以 L1也能有解决过拟合的效果。
3. L2正则化
L2正则化的损失函数:
![]()
正则化也有另外的一种表达形式:
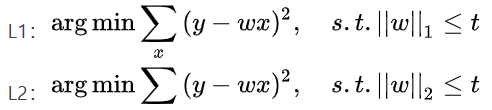
和L1画图的方式一样,当损失函数应用L2正则化时,图如下:
 可以看到与L1不同的是,L2在二维(两个变量)的图是个圆形。那么损失函数 J 的最优点就是圆形和等值线重合的地方,如上图黑点处。与L1相比,L2的“菱角”被磨平,因此L与J0相交时,
可以看到与L1不同的是,L2在二维(两个变量)的图是个圆形。那么损失函数 J 的最优点就是圆形和等值线重合的地方,如上图黑点处。与L1相比,L2的“菱角”被磨平,因此L与J0相交时,和
等于0的几率小了很多。所以L2正则化是不具有稀疏性的。
L2正则化为什么可以获得值很小的参数?
首先直观看一个例子:
设输入向量x=[1,1,1,1],两个权重向量w_1=[1,0,0,0],w_2=[0.25,0.25,0.25,0.25]。则。两个权重向量都得到同样的内积,但是
的L2惩罚是1.0,而
的L2惩罚是0.25。因此,根据L2惩罚来看,
更好,因为它的正则化损失更小。从直观上来看,这是因为
的权重值更小且更分散。所以L2正则化倾向于是特征分散,更小。
理论:
以线性回归中的梯度下降法为例。假设要求的参数为θ,是我们的假设函数。线性回归一般使用平方差损失函数。单个样本的平方差是
,,如果考虑所有样本,损失函数是对每个样本的平方差求和,假设有mmm个样本,线性回归的代价函数如下,为了后续处理方便,乘以一个常数
。
所以,未加正则项的损失函数如下:

在梯度下降算法中,需要先对参数求导,得到梯度。梯度本身是上升最快的方向,为了让损失尽可能小,沿梯度的负方向更新参数即可。
对于单个样本,先对某个参数求导:
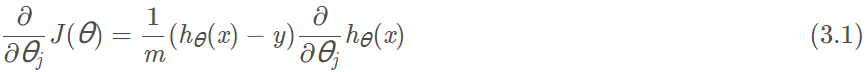
假设的表达式是:
. 单个样本对某个参数
求导,有
,最终(3.1)式结果如下:

在考虑所有样本的情况,将每个样本对的导数求和即可,得到下式:
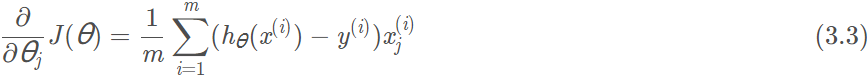
梯度下降算法中,为了尽快收敛,会沿梯度的负方向更新参数,因此在(3.3)式前添加一个负号,并乘以一个系数α(即学习率),得到最终用于迭代计算参数的形式:
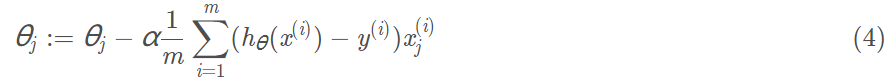
上式是没有添加L2正则化项的迭代公式.
如果在原始代价函数之后添加L2正则化,即:
求导后:
又在(3.2)已证:,所以有:
加入学习率α,得到最终加入L2正则后,用于迭代计算参数的形式:
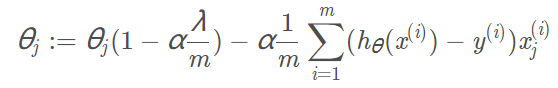
我们可以看到,每次迭代时,都会先乘上一个小于1的参数,那么
就会变量越来越小。
有人问:如果λ很大,变成一个很大的负数怎么办?不就越来越小啦?,这个我们看看,如果λ很大,那么正则化的区域就会非常小,由于L2正则化是一个圆,所以λ很大,那么圆就很小,甚至接近0,所以
多小都会有个极限的。

总结L2:
1. L2正则化倾向于是特征(权重)分散,更小
2. 没有特殊要求的情况下,能用L2就不用L1。
4. L2正则化在pytorch的应用
优化器采用Adam,并且设置参数weight_decay=10.0,即正则化项的权重等于10.0。
当weight_decay=0.0时,表示未使用正则化
optimizer = optim.Adam(model.parameters(),lr=learning_rate,weight_decay=10.0)但是pytorch目前的接口只支持L2正则化,不支持L1正则化
如果要用L1正则化,则需要手动实现:
regularization_loss = 0
for param in model.parameters():
regularization_loss += torch.sum(abs(param))
classify_loss = criterion(pred,target)
loss = classify_loss + lamda * regularization_loss
optimizer.zero_grad()
loss.backward()
optimizer.step()5. 结论性语言:
1. L1正则化容易产生稀疏权重矩阵,利于特征选择。也有一定的正则化能力;
2. L2正则化则倾向于生成权值较小的且分散的权值矩阵。生成的权值小的好处是,抗干扰性强,如果权值很大,那么可能数据移动(变化)了一点点,就会产生很大的偏差。有利于提高鲁棒性;
3. L1和L2都有提高泛化性能力,因为都是要解决过拟合问题;对于L2而言,会使得输入很大的输入变成小一点,使得模型抗干扰性强,因此有提高泛化能力的作用。
4. 没有特殊要求,能用L2就用L2;
5. L1正则化符合拉普拉斯分布,L2正则化符合高斯分布;
6. Reference
https://blog.csdn.net/jinping_shi/article/details/52433975
https://blog.csdn.net/lxlhexl/article/details/90712302
https://blog.csdn.net/liuweiyuxiang/article/details/99984288
























 996
996











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








