本人最近在学习DBN(Deep Belief Net,深度信念网络),通过学习才知道有RBM这个东西。因为我所要用到的DBN是有RBM通过累加堆叠组成的,要学习DBN就要弄明白RBM的原理。我就在此说一下我自己对RBM的认识和了解,同时也希望对别人有些帮助。
所谓受限玻尔兹曼机就是对玻尔兹曼机进行简化,使玻尔兹曼机更容易更简单地使用,原本玻尔兹曼机的隐元和显元之间是全连接的,而且隐元和隐元之间也是全连接的,这样增加了计算量和计算难度,使用困难。而RBM则是对BM进行一些限制,使隐元之间没有连接,这样就使得计算量大大减小,使用起来也就方便了很多。
RBM应用到了能量学上的一些知识:在能量最少的时候,物质最稳定。应用到RBM就是,在能量最少的时候,网络最稳定,也就是网络最优。
RBM有几个参数,一个是可视节点与隐藏节点直接的权重矩阵Wij,一个是可视节点的偏移量b = ( b1,b2,...,bn ),一个是隐藏节点的偏移量c = ( c1,c2,...,cm ).这几个参数决定了RBM网络将一个n维的样本编码成一个什么样的m维的样本。
下面为了方便,我们使用一个二进制的RBM来说一下原理吧。所谓二进制也就是隐元和显元的状态只能取1或0.这样它的能量函数为:
E(v,h)=−∑i=1n∑j=1mwijvihj−∑i=1nbivi−∑j=1mcjhj
在这个网络中,我们根据吉布斯(Gibbs)分布: p(v,h)=1Ze−E(v,h) 和上面的能量函数建立模型的联合概率分布.
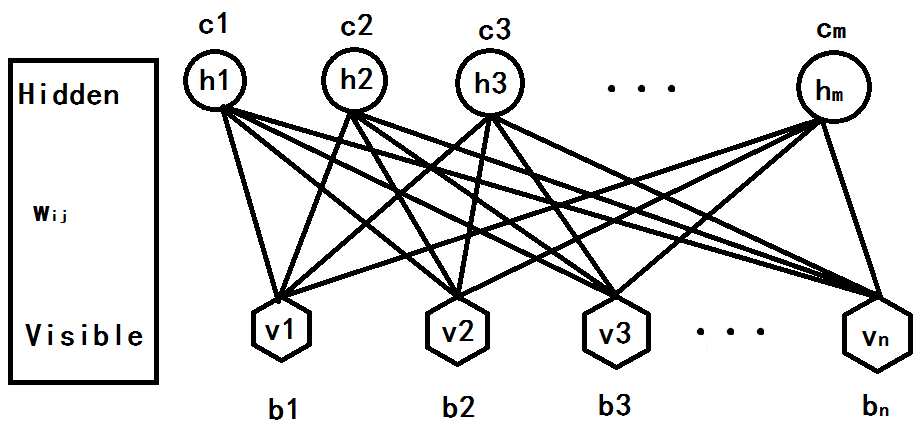
这是一张我自己画的一层RBM,这个网络有n个可视节点和m个隐藏节点,其中每个可视节点都只与m个隐藏节点相关,其它可视化节点相互独立,也就是这个可视节点的状态只受m个隐藏节点的影响,同理可知,对于每个隐藏节点也是如此,只受n个可视节点影响。也就是:
p(h|v)=∏i=1mp(hi|v)和p(v








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 9434
9434

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








