1前言
本篇博客主要记录两个分类模型(逻辑斯谛回归模型和最大熵模型)原理及模型的代码实现,将这两个模型放一块的原因是这两个模型都是对数线性模型,都是由条件概率分布表示P(Y|X).
这两种机器学习的算法的实例都是基于Titanic数据集,关于数据集的特征工程部分就不具体介绍,笔者在其他博文中已经详细描述了,此篇博客将直接使用已经经过特征工程处理后的数据集进行模型训练。
2逻辑斯谛回归模型
逻辑斯谛回归模型是建立在逻辑斯谛分布上的一种分类模型的,是可以解决多类别分类问题,属于概率模型。
2.1逻辑斯谛分布
假设X是随机变量,当X服从逻辑斯谛分布时,满足如下分布函数和概率密度函数:
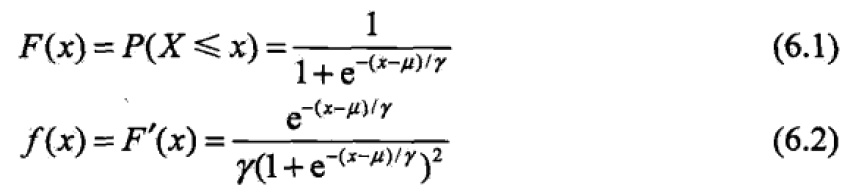
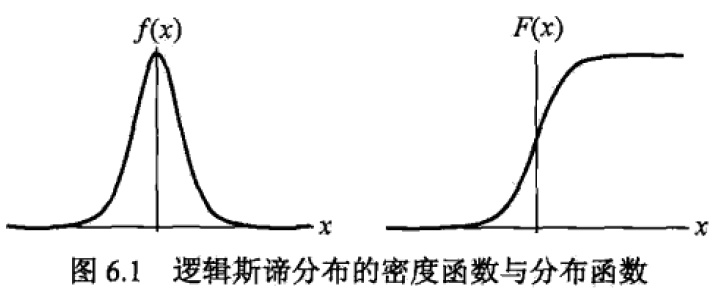
根据分布函数和概率密度函数可以画出图形如下,从图的右半部分概率分布函数来看,当随机变量X取值在μ值附近时,概率变化非常大。概率分布范围[0,1],且关于(μ,0.5)点对称。
2.2算法模型
此处主要讲解的是二分类问题,对应的算法模型是基于二项逻辑斯谛回归分布的条件概率模型。二项的意思是每次对于随机变量X的取值,Y有两种不同的结果Y={0,1}.当然如果是多分类问题的话,算法模型对应的是基于多(K)
项逻辑斯谛回归分布的条件概率。此时对于随机变量X的取值,Y有K中不同的结果Y={0,1,...,k}.
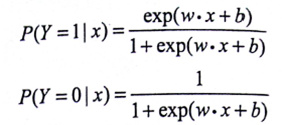
P是算法模型,为条件概率分布P(Y|X)。其中X为随机变量,对应着我们的样本。Y为样本归属的类别。使用算法模型对样本进行分类时,输入样本X,根据算法模型P,求出P(Y=0|X),P(Y=1|X)。比较P(Y=0|X),P(Y=1|X)大小,输出数值P条件概率大对应的类别。
2.3学习算法
学习算法主要用于求解算法模型,即求解P的过程。对于机器学习算法模型来说,一般都是通过先定义代价函数,再通过极小化代价函数的过程中,迭代求解出算法模型中的参数。对于算法模型是概率模型的,可以使用极大似然估计求解模型参数。当然也可以将负的似然函数理解成代价函数,通过极小化负的似然函数来求解出参数。
a.算法模型(其中π(x)代表逻辑斯谛回归分布函数):
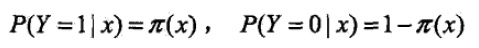
b.似然函数:
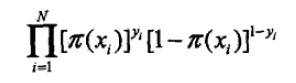
c.对数似然函数(将上面的似然函数进行取对数,由乘变为加法方便求导计算):
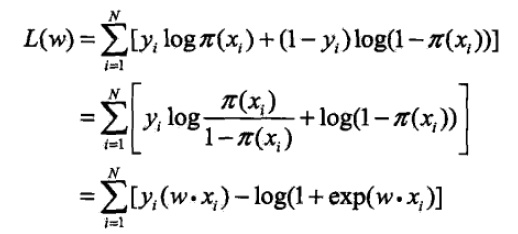
d.使用梯度下降法(迭代算法求解出模型参数),对数似然函数中变量是w.
2.4模型代码实现
# 主要代码,迭代求解,需要判断是否收敛
def train(self,train_X,train_y):
feature_size = train_X.shape[1]
sample_size = train_X.shape[0]
# 将w,b 融合了
self.w = np.zeros(feature_size + 1)
correct_num = 0
#梯度下降算法
for iter in range(self.maxIter):
# 随机选取一个样本
sample_index = random.randint(0,sample_size-1)
sample_select = train_X[sample_index].tolist()
sample_select.append(1.0)
sample_y = train_y[sample_index]
if sample_y == self.predict(sample_select):
# 连续预测对一定的数量
correct_num = correct_num + 1
if correct_num > self.maxIter:
break
continue
correct_num = 0
temp = np.exp(sum(self.w * sample_select))
for index in range(feature_size):
self.w[index] = self.w[index] - self.learn_late * \
(- sample_y * sample_select[index] + float(temp * sample_select[index])/float(1 + temp))
3最大熵模型
最大熵模型是一种用于分类的概率模型,它的思路是将最大熵原理应用到分类问题中。
3.1最大熵原理
1.对于概率模型的学习求解过程中,最大熵原理是一个准则。最大熵原理:学习概率模型时(求解概率模型参数时),在所有可能的概率模型中(所有可能的模型参数解)中,熵最大的模型是最好的模型(使得熵最大的模型参数是最终概率模型最好的参数)。
2.如何来确定可能的概率模型的集合?通常使用约束条件来确定概率模型的集合。这里的约束条件即是我们的特征函数——数据集中已有的事实。
熵最大的模型是最好的模型的原因:熵表示一个随机变量的不确定性,熵越大,表示随机变量越不确定,也就是随机变量越随机,对其行为做准确预测最困难。最大熵原理的实质就是,在已知部分知识的前提下,关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断,这是我们可以作出的唯一不偏不倚的选择,任何其它的选择都意味着我们增加了其它的约束和假设,这些约束和假设根据我们掌握的信息无法作出。
3.2最大熵模型的构建
最大熵模型: 对于一个分类模型,它的算法模型是一个概率模型P(Y|X),对于该概率模型的参数求解,采用的是基于最大熵原理进行选择最优的概率模型。
首先给定一个训练数据集T:
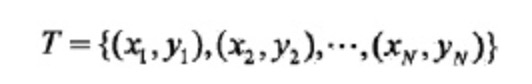
对于如何使用最大熵原理求解出该分类问题的概率模型参数,主要有以下几步:
Step1 提取出模型应该满足的约束条件然后表述成特征函数
特征函数f(x,y):

它描述的是模型的输入x和输出y之间的某一个事实,即对输入和输出同时抽取特征。
事实上满足的条件:理想的情况下最后的算法模型能够获取训练数据中的信息————对于最后求得的模型P(Y|X),特征函数f的期望和在训练集上特征函数f的期望理想情况上是相等的。
对于X,Y在数据集上的经验分布,可以得到经验联合分布P(X,Y)和经验边缘分布P(X),其中v(X=x,Y=y)表示样本(x,y)出现的次数,v(X=x)表示样本的输入为x的次数,N表示样本集的大小。
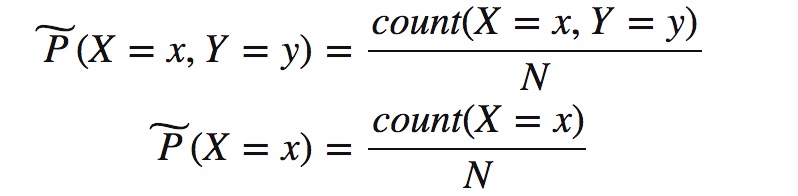
取训练集上特征函数f这一事实在经验分布P(X,Y)上的期望:
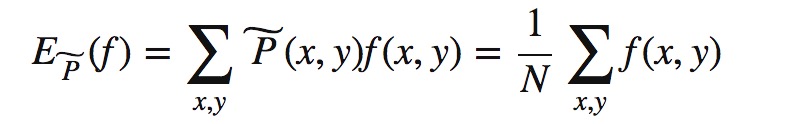
取特征函数在算法模型与经验分布上的期望:
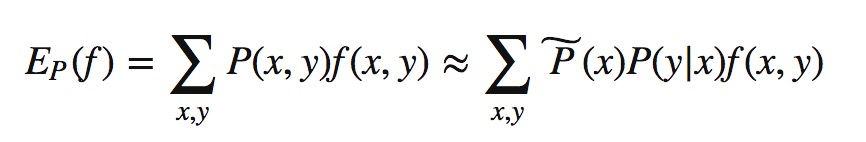
根据事实上满足的条件:
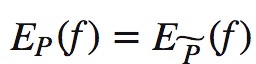
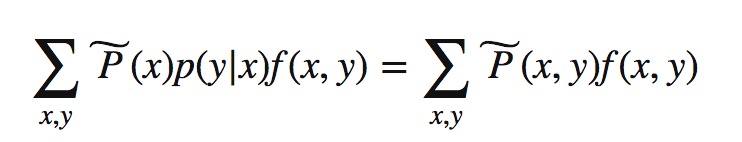
如果有N个事实(特征函数)就要N个约束条件,最后的算法模型需要满足这N个约束条件。
Step2 构建出满足所有约束条件的概率模型的集合
根据需要满足的N个约束条件构造出概率模型集合:
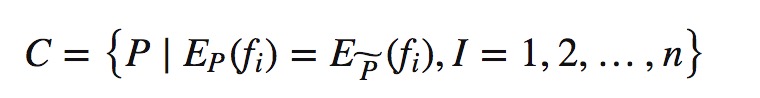
此时,我们的概率模型P(Y|X)在集合C中的条件熵为:
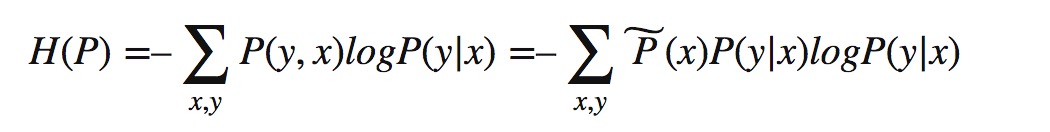
Step3 表述出概率模型的熵,并使之最大,求解出令该式子最大的模型
根据最大熵原理,可以列出式子求解出集合C中令概率模型熵最大的模型。于是我们的目标函数为:
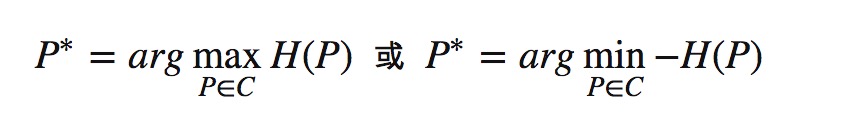
3.3学习算法
求解目标函数的过程也就是我们的学习算法,当然我们的目标函数需要满足事实上的一些条件:
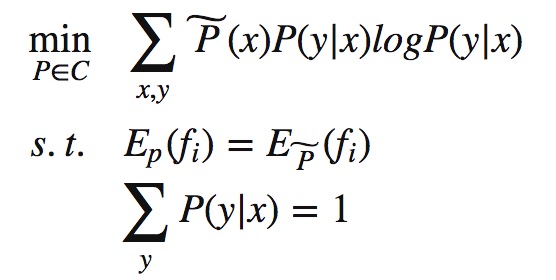
对应上式子,可以想到拉格朗日函数,来求解出极值。式中(w0,w1,…,wn为拉格朗日乘子)
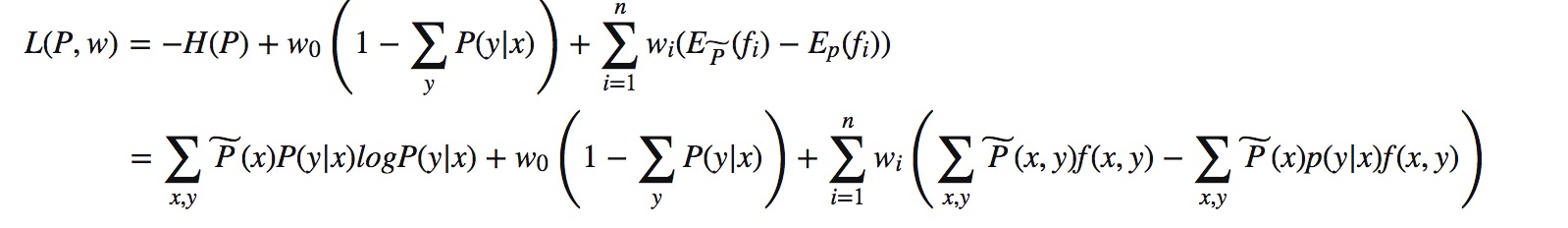
根据拉格朗日函数的对偶函数得出原始问题的形式为:
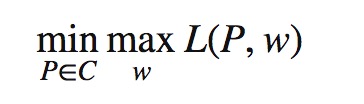
将原始问题进行对偶转换:
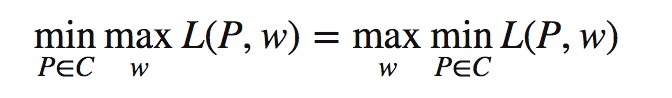
计算方式,先以w为定值计算关于P的极小,再进行计算关于w的极大值。
第一步:先以w为定值计算关于P的极小
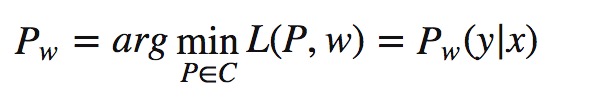
求极值,对参数求偏导,令等式等于0。
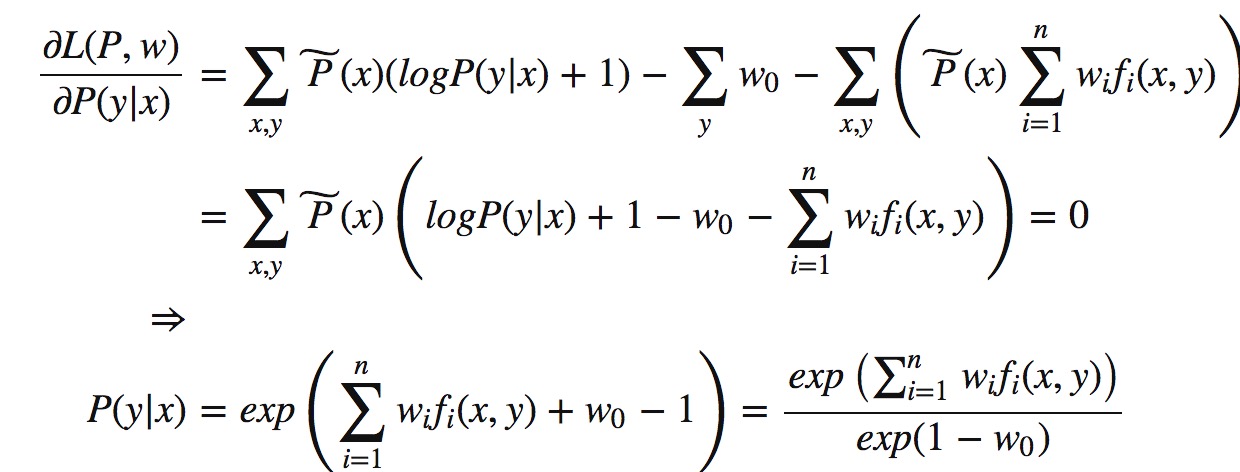

最后得:
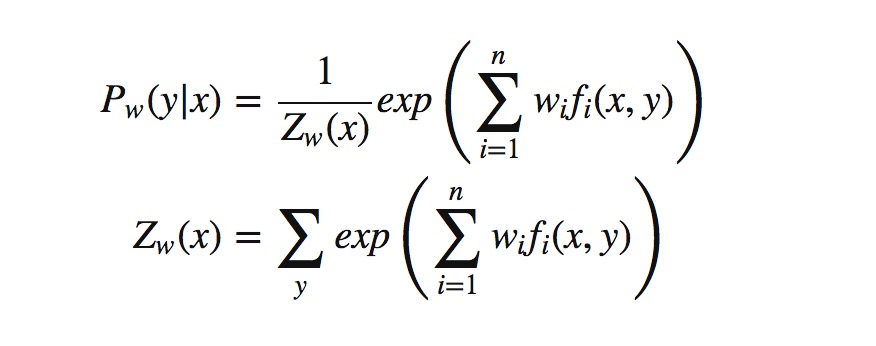
第二步:再进行计算关于w的极大值,其中ψ(x)表示第一步求解的最小值。
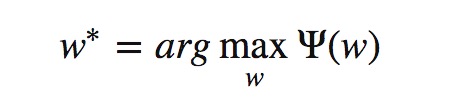
3.4模型代码实现——BFGS算法实现
def train(self,train_X,train_y):
# 使用《统计学习方法》P92算法6.2——BFGS,求解参数
self.feature_size = train_X.shape[1]
self.sample_num = train_X.shape[0]
self.samples = train_X
self.labels = train_y
# 统计数据集中的特征函数个数
self._cal_feature_func()
self._f2id()
self.n = len(self.P_x_y) # n为特征函数的个数
# 计算每个特征函数关于经验分布p(x,y)的期望,并保持于EPxy字典中
self._cal_EPxy()
self.w = np.zeros(self.n) #wi为拉格函数中的乘子
self.g = np.zeros(self.n) #对应g(w),《统计学习方法》P92,最上面g(w)的公式
self.B = np.eye(self.n) #正定对称矩阵
for iter in range(self.maxIter):
# 算法6.2——(2)
self._cal_Gw()
if self._cal_g_l2() < self.epsion:
break
# 算法6.2——(3)
p_k = - (self.B ** -1) * np.reshape(self.g,(self.n,1))
# np.linalg.solve()
# 算法6.2——(4)
r_k = self._liear_search(p_k)
# 算法6.2——(5)
old_g = copy.deepcopy(self.g)
old_w = copy.deepcopy(self.w)
self.w = self.w + r_k * p_k
# 算法6.2——(6)
self._cal_Gw()
if self._cal_g_l2() < self.epsion:
break
y_k = self.g - old_g
fai_k = self.w - old_w
y_k = np.reshape(y_k,(self.n,1))
fai_k = np.reshape(fai_k,(self.n,1))
temp1 = np.dot(y_k,y_k.T) / float((np.dot(y_k.T,fai_k).reshape(1)[0]))
temp2 = np.dot(np.dot(np.dot(self.B,fai_k),fai_k.T),self.B) / float(np.dot(np.dot(fai_k.T,self.B),fai_k).reshape(1)[0])
self.B =self.B + temp1 - temp2
代码说明: # 算法6.2——(4)r_k = self._liear_search(p_k) 求步长r_k的过程中是需要满足如下条件:
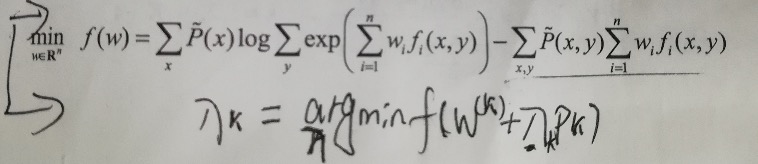
其中,求r_k的思路是:因为p_k和w_k是已知的,r_k未知,所以求f对r_k求导,令导数为0,求出r_k。此处求导极为复杂,不知道其他大神有什么简便求解算法,忘告知,感谢。
4总结
1.最大熵模型和逻辑斯谛回归模型对于求解分类问题都是概率模型P(Y|X).对概率模型的求解方式,都可以使用极大似然估计方法求参数。
2.最大熵模型的关键是需要将分类问题建立在最大熵原理上,从而构建出一个凸优化问题。第二个关键点是特征函数的抽取的过程中,是相当于在优化问题上附加了约束条件。这时候对参数的求解就是带约束条件的凸优化问题,需要引入拉格朗日函数进行求解。将原始问题进行对偶转换。这点与线性支持向量机的参数求解相似,都是带约束条件的凸优化问题。























 1180
1180











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








