神经网络压缩是人工智能落地过程中重要的一个环节。关于网络压缩的理论之前就已经有很多,比如,模型蒸馏,剪枝,量化,低秩矩阵近似等。彩票理论算是个令人耳目一新的观点,值得看看。
摘要:
神经网络修剪技术可以将训练有素的网络的参数数量减少90%以上,减少存储需求并提高推理的计算性能,而不会影响准确性。 但是,当代的经验是,修剪产生的稀疏架构从一开始就很难训练,这同样会提高训练性能。发现,标准的修剪技术自然会发现子网,这些子网的初始化使其能够有效地进行训练。 根据这些结果,提出彩票假设:密集的,随机初始化的前馈网络包含子网(赢得彩票),这些子网经过单独训练后,在相似的迭代次数中可以达到与原始网络相当的测试精度。 所发现的中奖彩票已经获得了初始化彩票:他们的连接具有使训练特别有效的初始权重。本文提出了一种识别中奖彩票的算法,以及一系列支持彩票假设和这些偶然初始化的重要性的实验。 始终发现中奖彩票的大小不到MNIST和CIFAR10的几种全连接和卷积前馈体系结构的大小的10-20%。 超过此大小,并发现的中奖彩票比原始网络学习得更快,并且达到更高的测试准确性。
1. 简介
如果一个网络的规模可以缩小,为什么我们不训练这个更小的架构,而是为了提高训练的效率呢?当前的经验是,通过修剪发现的架构从一开始就很难进行培训,其准确性低于原始的网络。
考虑如下例子,
我们从用于MNIST的全连接网络和用于CIFAR10的卷积网络中随机采样和训练子网。 随机抽样模拟了LeCun等人使用的非结构化修剪的效果。在稀疏性的各个级别上,虚线跟踪了最小验证损失的迭代以及该迭代时的测试准确性。结果表明,网络稀疏,学习速度越慢,最终的测试准确性越低。

然而,作者表明,始终存在着较小的子网,它们从一开始就进行训练,并且学习速度至少与较大的子网一样快,同时达到了相似的测试精度。 图1中的实线显示了我们找到的网络。 基于这些结果,我们陈述彩票假设,
随机初始化的密集神经网络包含一个已初始化的子网络,以便在单独训练子网络时,在经过最多相同数量的迭代训练后,可以匹配原始网络的测试精度。
以下是公式说明,

识别中奖彩票
我们通过训练网络并修剪其最小幅度权重来确定中奖彩票。 其余未修剪的连接构成了中奖彩票的体系结构。 对于我们的工作而言,独特的是,每个未修剪的连接的值都将在经过培训之前从原始网络重置为其初始化。以下是重要步骤,

如上所述,这种修剪方法是一次性的:对网络进行一次训练,修剪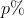 %的权重,并重置剩余的权重。 但是,在本文中,我们将重点放在迭代修剪上,它反复训练,修剪和重置网络周围的环境。 每一轮的重量都应减去前一轮的
%的权重,并重置剩余的权重。 但是,在本文中,我们将重点放在迭代修剪上,它反复训练,修剪和重置网络周围的环境。 每一轮的重量都应减去前一轮的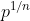 %重量。 我们的结果表明,与一次修剪相比,迭代修剪可以找到与原始网络的精度相匹配的中奖票证。
%重量。 我们的结果表明,与一次修剪相比,迭代修剪可以找到与原始网络的精度相匹配的中奖票证。
结果
我们通过多种优化策略(SGD,动量和Adam)在MNIST的全连接体系结构和CIFAR10的卷积体系结构中识别中奖票证,这些技术具有dropout,weight decay,batch normal和residual connections等技术。 我们使用非结构化剪枝技术,因此这些中奖票证是稀疏的。 在更深入的网络结构中,我们基于剪枝的寻找中奖彩票的策略对学习率敏感:需要热身才能找到中奖彩票。我们找到的中奖彩票是原始网络的10%~20%。减小到此大小后,它们最多可以在相同的迭代次数(相应的训练时间)内达到或超过原始网络的测试精度(相称的准确性)。随机重新初始化后,中奖彩票的表现将更差,这意味着仅凭结构无法解释中奖彩票的成功。
彩票猜想
回到我们的激励问题,我们将假设扩展到一个未经检验的猜想,即SGD会寻找并训练一部分初始化良好的权重。 密集的,随机初始化的网络比修剪导致的稀疏网络更容易训练,因为存在更多可能的子网络,训练可以从中回收中奖票。
本文贡献
- 我们证明,剪枝发现了可训练的子网,这些子网在相同的迭代次数中即可达到与原始网络相当的测试精度。
- 我们表明,剪枝发现的获胜票证比原始网络学习得更快,同时达到了更高的测试精度和泛化能力更好。
- 我们提出彩票假设作为神经网络组成的新观点来解释这些发现
在本文中,我们对彩票假设进行了实证研究。 现在我们已经演示了中奖彩票的存在,我们希望利用这一知识来,
- 提升训练性能。由于可以从一开始就对中奖彩票进行单独培训,因此希望我们可以设计出训练方案,以尽早搜索中奖彩票和剪枝。
- 设计更好的网络。中奖彩票揭示了稀疏架构和初始化的组合 特别善于学习。 我们可以从中奖券中汲取灵感,设计出具有与学习相同属性的新架构和初始化方案。 我们甚至可以将为一项任务发现的中奖彩票转移给其他许多人。
- 提高了我们对神经网络的理论理解。我们可以研究为什么随机初始化的前馈网络似乎包含中奖彩票以及对优化理论研究的潜在影响
2.全连接网络中的中奖彩票
在本节中,我们评估了应用于MNIST训练的全连接网络的彩票假设。 我们使用Lenet-300-100架构,如图2所示。我们遵循第1节的概述:在随机初始化和训练网络之后,我们修剪网络并将剩余的连接重置为其原始连接的初始化值。我们使用简单的逐层修剪启发式方法:删除每一层中具有最低幅度的权重的百分比。与输出的连接修剪速度为网络其余部分速率的一半。

![]()
迭代剪枝
图3 刻画了迭代修剪再不同程度的中奖彩票时的平均测试准确性。在第一轮修剪中,网络修剪得越多,网络学习速度就会越快,测试精度也越高(图3中的左图)。 包含原始网络权重的51.3%(即Pm = 51.3%)的中奖票证比原始网络更快地达到更高的测试准确性,但比Pm = 21.1%时要慢。 当Pm <21.1%时,学习变慢(中图)。 当Pm = 3.6%时,中奖彩票将还原为原始网络的性能。 在整个本文中都重复了类似的模式。

随机重新初始化
为了衡量中奖彩票初始化的重要性,我们保留了中奖彩票的结构(即maskm),但随机采样了一个新的初始化θ′0〜Dθ。我们将每张中奖彩票随机地重新初始化三次,使得每点总数为15 4.我们认为初始化对于中奖彩票的有效性至关重要。 图3的右图显示了此迭代修剪实验。 除了原始网络和Pm = 51%和21%的中奖彩票之外,还有随机重新初始化实验。 修剪后中奖彩票的学习速度更快,而随机重新初始化时,它们的学习速度则逐渐变慢。
该实验的更广泛的结果是图4a中的橙色线。 与中奖票券不同,重新初始化的网络学习速度比原始网络慢,并且在修剪后会失去测试准确性。 当Pm = 21.1%时,重新初始化的迭代中奖彩票的平均测试准确性从原始准确性下降,而中奖彩票的2.9%。 当Pm = 21%时,中奖彩票的最小验证损失比重新初始化时快2.51倍,并且准确度降低了半个百分点。 Pm≥5%时,所有网络的训练精度均达到100%;此实验支持彩票假设强调初始化:原始的初始化可从修剪中受益并受益,而随机重新初始化的性能会立即受到影响并稳定下降
一次剪枝
尽管迭代修剪可提取较小的中奖彩票,但重复训练意味着找到它们的成本很高。 一键式修剪使无需重新培训即可确定中奖彩票。 图4c显示了一次修剪(绿色)和随机重新初始化(红色)的结果; 一次性修剪确实可以找到中奖彩票。 当67.5%≥Pm≥17.6%时,平均中奖彩票的验证准确性要比原始网络更早。当95.0%≥Pm≥5.17%时,测试准确性要高于原始网络。 但是,以迭代方式修剪的中奖彩票学习速度更快,并且在较小的网络规模下可以达到更高的测试准确性。 在图4a的对数轴上复制了图4c中的绿线和红线,使该性能差距清晰可见。 由于我们的目标是确定最小的中奖彩票,因此在本文的其余部分中,我们将重点放在迭代修剪上。

3.卷积神经网络上的中奖彩票
在这里,我们将彩票假设应用于CIFAR10上的卷积网络,这既增加了学习问题的复杂性,又增加了网络的规模。 我们考虑图2中的Conv-2,Conv-4和Conv-6架构,它们是VGG系列的按比例缩小的变体。 网络有两个,四个或六个卷积层,后面是两个完全连接的层; 最大卷积发生在每两个卷积层之后。 这些网络涵盖了从几乎完全连接到传统的卷积网络的范围,在Conv-2中卷积层中的参数不到1%,在Conv-6中近三分之二。
寻找中奖彩票

图5(顶部)中的实线显示了Conv-2(蓝色),Conv-4(橙色)和Conv-6(绿色)在图2的逐层修剪速率下的迭代彩票实验。 Lenet在第2节中重复:修剪网络后,与原始网络相比,它学习速度更快,测试准确性也有所提高。 在这种情况下,结果更加明显。对于Conv-2(Pm = 8.8%),中奖票证达到最小验证损失的最快速度是3.5倍;对于Conv-4(Pm = 9.2%),票证可以达到3.5倍;对于Conv-6(Pm = 15.1%),票证可以达到2.5倍。 Conv-2(Pm = 4.6%),Conv-4(Pm = 11.1%),3.5和Conv-6(Pm = 26.4%)的测试精度最高提高3.4个百分点。所有三个网络均保持高于原始水平 Pm> 2%时的平均测试准确度。如第2节中所述,提前停止迭代时的训练准确度随测试准确度而提高。 但是,对于Conv-2,迭代20,000,对于Conv-4,迭代25,000,对于Conv-6,迭代30,000(与原始网络的最终训练迭代相对应的迭代),当Pm≥2%时,所有网络的训练精度均达到100%(附录D, 图13)和中奖彩票仍保持较高的测试准确性(右下图5)。 这意味着测试和培训准确度之间的差距较小,这表明票证的泛化效果更好
与第2节中一样,提早停止迭代的训练准确性随测试准确性而提高。 但是,对于Conv-2,迭代20,000,对于Conv-4,迭代25,000,对于Conv-6,迭代30,000(与原始网络的最终训练迭代相对应的迭代),当Pm≥2%时,所有网络的训练精度均达到100%(附录D, 图13)和中奖彩票仍保持较高的测试准确性(右下图5)。 这意味着测试和培训准确性之间的差距较小,可以更好地概括票证。








 研究发现,神经网络中存在“中奖彩票”——特定的子网络,即使从头开始训练,也能达到与完整网络相当的性能。这些子网络具有特殊的初始化权重,使它们能够高效学习。通过迭代修剪和重置权重,可以识别这些中奖彩票,从而实现网络压缩,提高计算效率和存储效率。
研究发现,神经网络中存在“中奖彩票”——特定的子网络,即使从头开始训练,也能达到与完整网络相当的性能。这些子网络具有特殊的初始化权重,使它们能够高效学习。通过迭代修剪和重置权重,可以识别这些中奖彩票,从而实现网络压缩,提高计算效率和存储效率。
















 57
57

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








