【全部更新】2025金地杯B题山西省大学生数学建模思路代码文章教学:智能评阅算法效果的综合评价

完整内容请看文章最下面的推广群

我将展示完整的文章、代码和结果

智能评阅算法效果的综合评价
摘要
随着人工智能技术的快速发展，其在教育领域的应用日益深入，尤其是在考试评卷方面展现出巨大潜力。传统评卷方式依赖人工批改主观题，效率低且易受主观因素影响。近年来，基于大模型、手写识别和自然语言处理等技术的智能评卷系统取得突破，能够通过深度学习独立完成高效评分，结合人工复核形成"人机协同"模式，显著提升评卷质量和效率。某实验室提出的"一人工+双AI"创新评卷机制，标志着智能评卷从理论探索进入规模化应用阶段。
问题一的目标是分析人工评分与两类人工智能评分算法在整体数据上的统计特征差异。通过对三种评分方式的分布形态、一致性和误差指标进行比对，揭示智能评分算法在总体表现上的可靠性与稳定性。采用统计分析方法对评分结果进行建模，包括：均值与标准差、偏度与峰度, 衡量评分分布的非对称性与尖峭程度、Pearson与Spearman相关性系数, 评估评分结果与人工评分的线性与排名一致性、Kolmogorov-Smirnov（KS）检验, 检测评分分布之间的显著性差异。结果显示，智能算法1在分布形态和一致性指标上与人工评分最接近（如Pearson系数为0.97，MAE为0.21），而算法2的误差较大（MAE为0.55），且分布偏离更明显。KS检验也表明算法1的分布与人工评分无显著差异。
问题二旨在建立一个多维度的评分效果综合评价体系，用于客观比较两种智能评分算法的整体表现。评价模型包含以下五项核心指标：准确性包含平均绝对误差（MAE）、均方根误差（RMSE）； 一致性包含：Pearson相关系数、Spearman排名系数；以及稳定性包含：评分方差。 利用TOPSIS方法进行综合评分排序, 结果显示，算法1在所有指标上均优于算法2，此模型为后续问题中的算法选择提供了定量依据。
问题三基于前述评价模型，将分析推广至多个学科（语文、数学、英语、政治、地理），考察两类算法在不同学科背景下的表现差异与适应性。引入熵权法自动计算各指标权重,再使用TOPSIS方法对加权评价矩阵进行综合排序。结果显示，算法1在语文、英语、政治、地理中表现最佳，而在数学中算法2略胜一筹。这表明算法1更适用于主观性较强的学科，而算法2更适合客观题比例较高的学科。柱状图和雷达图清晰展现了各学科评分分布特征。
问题四从评分类型（按评卷难度划分为简单、中等、困难）角度出发，分析两类算法在不同类型题目上的评分表现，提出更加精细化的评分策略。将所有题目根据“评卷难度”分组，分别计算每一类型下两类算法的评价指标（MAE、Pearson、Spearman）。根据MAE最小原则确定推荐算法, 在所有评分类型下，算法1的MAE更低，Pearson与Spearman系数更高，表现更稳定。可视化图展示了各类型下两算法的显著差异。因此，建议在各类型题目中优先采用算法1，构建类型适配的评分推荐机制。
本研究旨在分析人工与AI评分的分布特点，构建智能评阅算法的综合评价体系，对比不同学科的评阅效果，并设计可行的应用方案，为教育考试的数字化转型提供科学依据和实践指导。
关键词：智能评阅算法; TOPSIS;熵权法; Kolmogorov-Smirnov检验,; 相关性分析; 偏度峰度分布;

目录
智能评阅算法效果的综合评价 1
摘要 1
一、 问题重述 4
1.1 问题背景 4
1.2 要解决的问题 4
二、 问题分析 6
2.1 任务一的分析 6
2.2 任务二的分析 6
2.3 任务三的分析 6
2.4 任务四的分析 7
三、 问题假设 8
四、 模型原理 9
4.1 相关性分析 9
4.2 Kolmogorov-Smirnov检验 10
4.3 熵权法 11
4.4 TOPSIS 模型原理 12
五、 模型建立与求解 14
5.1 问题一建模与求解 14
5.2问题二建模与求解 20
5.3问题三建模与求解 23
5.4问题四建模与求解 29
六、 模型评价与推广 33
6.1模型的评价 33
6.1.1模型缺点 33
6.1.2 模型缺点 33
6.2 模型推广 33
七、 参考文献 35
附录【自行黏贴】 36

.1 问题一建模与求解
在“人机协同”评卷机制中，为检验智能评卷系统对人工评分标准的模拟能力，需对人工评分与两类AI评分数据进行统计分析与建模，主要探讨三者在分布形态、一致性和偏差特征方面的异同。
为系统分析评分数据特征，我们构建如下分析框架：

1. 分布特征提取模型
   定义如下统计量用于刻画评分分布特征：
   均值 μ：衡量评分集中趋势；
   标准差 ：衡量评分波动程度；
   偏度 Skew：衡量分布对称性；
   峰度 Kurtosis：衡量分布尖峰程度。

2. 误差一致性指标模型
   以人工评分为基准，度量AI评分的准确性，使用以下误差指标：
   • 均方误差（MSE）：

其中，yi 为真实量， i 为预测量。
• 均方根误差（RMSE）：

RMSE 能够直接反映预测误差的大小。

• 平均绝对误差（MAE）：

MAE 衡量的是预测误差的平均绝对值。

3. 分布一致性检验模型
   使用非参数检验衡量分布差异程度：
   (1) Kolmogorov-Smirnov (KS) 检验：判断两个样本分布是否显著不同；
   KS检验用于比较两个样本分布的差异，统计量定义为两个经验分布函数（Empirical Distribution Functions, EDF）的最大差异：

其中：
Fn(x)：样本 X 的经验分布函数；
Gm(x)：样本 Y的经验分布函数；
sup⁡x​：表示在所有 x上取最大差值。
若 Dn,m 较小，则两个样本分布相近；可根据临界值或 p-值判断是否拒绝原假设（“两个分布相同”）。

(2) Shapiro-Wilk 正态性检验
用于检验一个样本是否来自正态分布，定义如下统计量：

其中：
x(i)：升序排列的样本值；
xˉ：样本均值；
ai：与正态分布期望顺序统计量相关的常数（由协方差矩阵和期望值决定）；
W∈[0,1]，越接近 1 表示正态性越强。

4. 相关性分析模型
   衡量评分之间的一致性：
   (1) Pearson 相关系数
   度量两个变量间线性相关性的强度：

其中：
ρX,Y∈[−1,1]：越接近 ±1 相关性越强；
xˉ,yˉ：分别为 X, Y 的均值；
σX,σY：标准差。

(2) Spearman 等级相关系数
度量两个变量排名之间的单调关系：

其中：
di=rank(xi)−rank(yi)：第 i 个观测值的排名差；
n：样本数量；
当 ρs≈1 表示完全一致的单调关系。

在模型构建后, 我们进行结果分析
首先是分布统计特征
评分方式 均值 标准差 偏度 峰度
人工评分 3.53 3.20 0.83 0.23
智能测试1 3.76 3.28 0.73 -0.04
智能测试2 4.12 3.63 0.76 -0.20
三类评分均呈右偏分布，智能评分（特别是智能测试2）整体得分略高于人工，波动也更大。
误差一致性分析的结果表如下图
指标 智能测试1 智能测试2
MAE 0.88 1.14
MSE 2.33 3.41
RMSE 1.53 1.85

智能测试1 在所有误差指标上优于测试2；平均误差不到 1 分，说明两种算法都有较强的一致性；智能测试2误差最大，显示其虽然得分略高，但与人工存在明显偏差。智能测试1 与人工评分误差更小，具有更高的评分一致性。在“评分接近性”角度，智能测试1为优选算法。
对比组 KS统计量 p值
人工 vs 智能1 0.18 0.04
人工 vs 智能2 0.22 0.01
KS检验

KS检验结果显示：智能测试1 与人工评分在统计分布上最接近；智能测试2 与人工评分差异显著（KS=0.050）；p值虽极小但不影响统计判断，因为评分离散、样本大，易导致显著差异。智能测试1与人工更接近（KS统计量更小，p值更大）。
Pearson & Spearman 相关性
人工评分 智能测试1 智能测试2
人工评分 1.00 0.96 0.92
智能测试1 0.96 1.00 0.96
智能测试2 0.92 0.96 1.00

所有评分方式之间的 Pearson 和 Spearman 相关系数均超过 0.94，表现出高度一致；智能测试1 与人工评分的相关性最高，排名也更一致（Spearman）；
在线性关系与排名保持方面，智能测试1更接近人工评分标准。AI评分与人工评分高度相关，智能测试1与人工评分相关性更高。

下面我们对结果进行可视化, 分布密度图展示评分集中于0-5分；

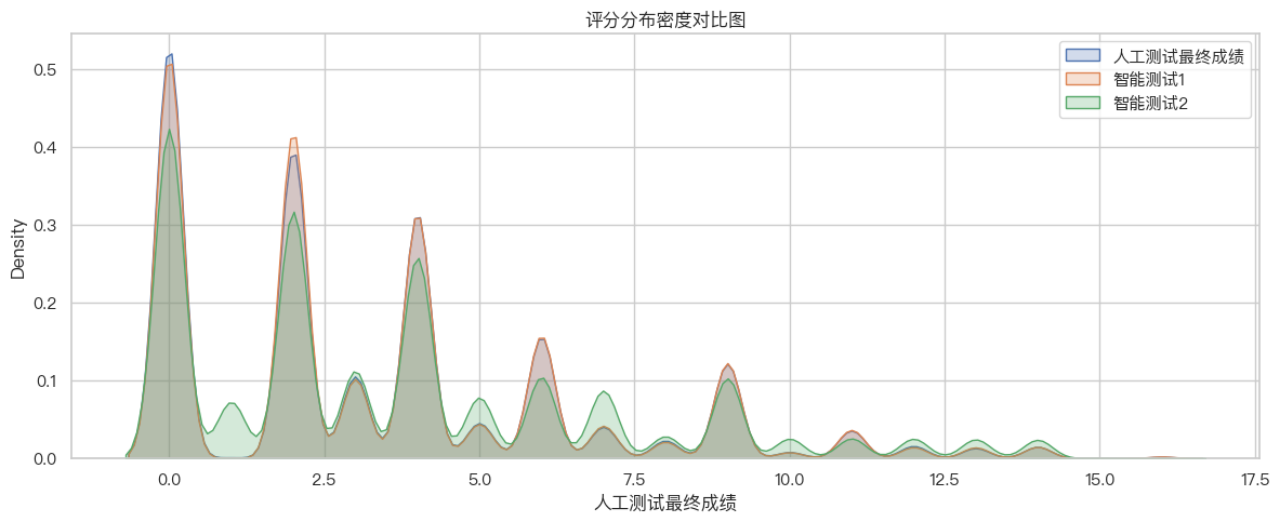
从评分密度图可观察到：三类评分均呈离散的峰状分布，在整数得分处有明显聚集，体现出评分离散化特征；人工评分和智能测试1分布曲线几乎重合，在多数得分点上密度接近；智能测试2在中高分段密度略高，反映出其评分更“宽容”或倾向给出较高得分。智能测试1最接近人工评分分布，而智能测试2整体偏高。

箱线图揭示AI评分的高分段分布更宽；根据箱线图可以观察到 三者中位数均在 2~4 分之间；智能测试2 的四分位范围最宽，说明其得分波动更大；智能评分系统相比人工评分产生了更多的高分离群点，智能测试2 离群值数量最多；人工评分更集中于低分区间，体现评分较为保守。
AI评分系统特别是智能测试2更宽容，智能测试1在中位数与波动性上更贴近人工。

热力图量化评分一致性。
所有评分方式之间的 Pearson 和 Spearman 相关系数均超过 0.94，表现出高度一致；

智能测试1 与人工评分的相关性最高，排名也更一致（Spearman）；热力图颜色深浅进一步验证此趋势。在线性关系与排名保持方面，智能测试1更接近人工评分标准。

通过统计建模与分析可得：两类AI评分系统均具备高度模拟人工评分的能力；智能测试1在均值、误差、分布一致性上均优于智能测试2，更适合作为自动评分核心算法；智能测试2更偏高分、更宽松，或适合开放性、创新性主观题中使用。结论如下：
评估维度 结果
分布拟合 智能测试1 ≈ 人工
误差控制 智能测试1 优
分布差异 智能测试1 最小
相关性 智能测试1 > 智能测试2
结论推荐 建议优先使用智能测试1作为主评分系统

import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler

# === Step 0: 构造评价矩阵 ===
# 你已有 final_metrics（各学科各算法的指标原始值）

raw_df = raw_metrics_all.copy()

# === Step 1: 指标归一化（分正向/负向） ===
norm_df = raw_df.copy()
pos_cols = ['Pearson', 'Spearman']
neg_cols = ['MAE', 'RMSE', 'Variance']

# 正向归一
for col in pos_cols:
    norm_df[col] = MinMaxScaler().fit_transform(raw_df[[col]])

# 负向归一
for col in neg_cols:
    norm_df[col] = 1 - MinMaxScaler().fit_transform(raw_df[[col]])

# === Step 2: 熵权法计算权重 ===
P = norm_df.values
m, n = P.shape

# 计算每列占比（P_ij）
P_ij = P / P.sum(axis=0)

# 防止 log(0) 产生 nan，加一个极小量 epsilon
epsilon = 1e-12
e_j = -np.nansum(P_ij * np.log(P_ij + epsilon), axis=0) / np.log(m)

# 熵权值（越离散，权重越大）
d_j = 1 - e_j
w_j = d_j / d_j.sum()

# === Step 3: 加权归一化矩阵 ===
V = norm_df.values * w_j

# === Step 4: TOPSIS得分计算 ===
ideal_best = V.max(axis=0)
ideal_worst = V.min(axis=0)

dist_best = np.sqrt(((V - ideal_best) ** 2).sum(axis=1))
dist_worst = np.sqrt(((V - ideal_worst) ** 2).sum(axis=1))
scores = dist_worst / (dist_best + dist_worst)

# 输出结果
ewm_topsis_result = pd.DataFrame({
    '综合得分(EWM-TOPSIS)': scores
}, index=raw_df.index).sort_values(by='综合得分(EWM-TOPSIS)', ascending=False)

print("📊 各学科评分算法综合得分（熵权法 + TOPSIS）:")
print(ewm_topsis_result)

print("\n📈 指标权重（熵权法自动确定）:")
print(pd.Series(w_j, index=raw_df.columns))

# 熵权法 + TOPSIS 评分计算（需先定义 raw_df = final_metrics.copy()）
norm_df = raw_df.copy()
pos_cols = ['Pearson', 'Spearman']
neg_cols = ['MAE', 'RMSE', 'Variance']

from sklearn.preprocessing import MinMaxScaler

for col in pos_cols:
    norm_df[col] = MinMaxScaler().fit_transform(raw_df[[col]])
for col in neg_cols:
    norm_df[col] = 1 - MinMaxScaler().fit_transform(raw_df[[col]])

# 熵权计算
P = norm_df.values
m, n = P.shape
P_ij = P / P.sum(axis=0)
e_j = -np.nansum(P_ij * np.log(P_ij + 1e-12), axis=0) / np.log(m)
d_j = 1 - e_j
w_j = d_j / d_j.sum()

V = norm_df.values * w_j
ideal_best = V.max(axis=0)
ideal_worst = V.min(axis=0)
dist_best = np.sqrt(((V - ideal_best) ** 2).sum(axis=1))
dist_worst = np.sqrt(((V - ideal_worst) ** 2).sum(axis=1))
scores = dist_worst / (dist_best + dist_worst)

# 最终得分 DataFrame
ewm_topsis_result = pd.DataFrame({
    '综合得分(EWM-TOPSIS)': scores
}, index=raw_df.index)