mpc模型预测控制从原理到代码实现mpc模型预测控制详细原理推导

mpc模型预测控制从原理到代码实现
mpc模型预测控制详细原理推导
matlab和c++两种编程实现
四个实际控制工程案例：
双积分控制系统
倒立摆控制系统
车辆运动学跟踪控制系统
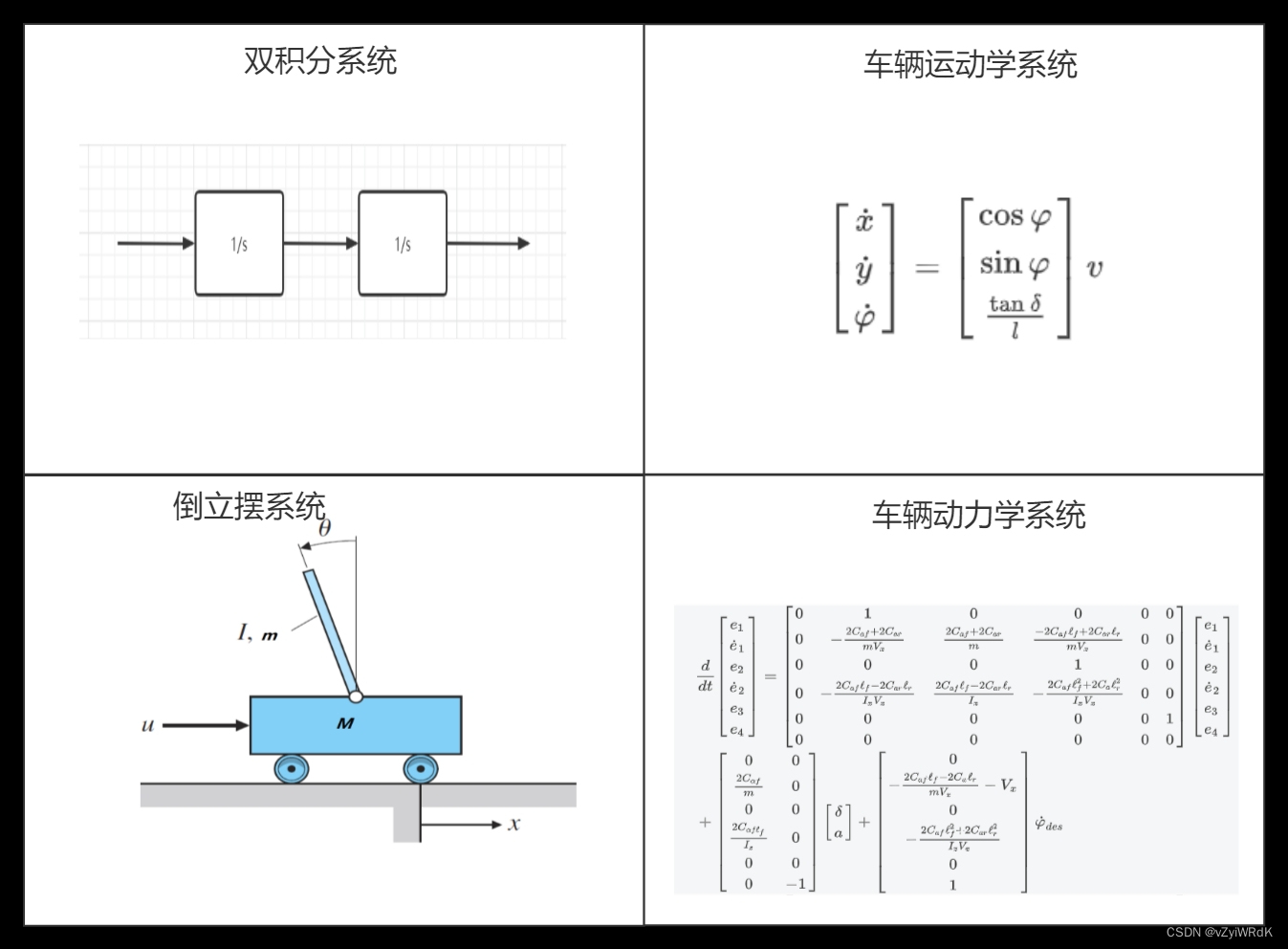
车辆动力学跟踪控制系统
包含上述所有的文档和代码。

MPC模型预测控制从原理到代码实现

MPC模型预测控制是一种高级控制技术，它能够通过对系统未来行为的预测来实现对系统的控制，因此被广泛应用于各种需要高精度控制的场景，比如机器人控制、飞行器控制、汽车控制等。在本篇文章中，我们将会详细地介绍MPC模型预测控制的原理以及如何使用Matlab和C++两种编程语言来实现MPC控制器。同时，我们还将提供四个实际控制工程案例，分别是双积分控制系统、倒立摆控制系统、车辆运动学跟踪控制系统和车辆动力学跟踪控制系统。在这些案例中，我们将会根据实际应用需求来演示MPC模型预测控制的实现方法，并提供相应的文档和代码。

一、MPC模型预测控制详细原理推导

MPC模型预测控制的核心思想是通过对系统未来的一系列状态预测，来确定当前时刻的最优控制策略。具体来说，MPC将控制问题转化为优化问题，通过求解最优化问题得到当前时刻的最优控制指令。MPC的控制策略可以被描述为以下三个步骤：

1. 预测模型建立

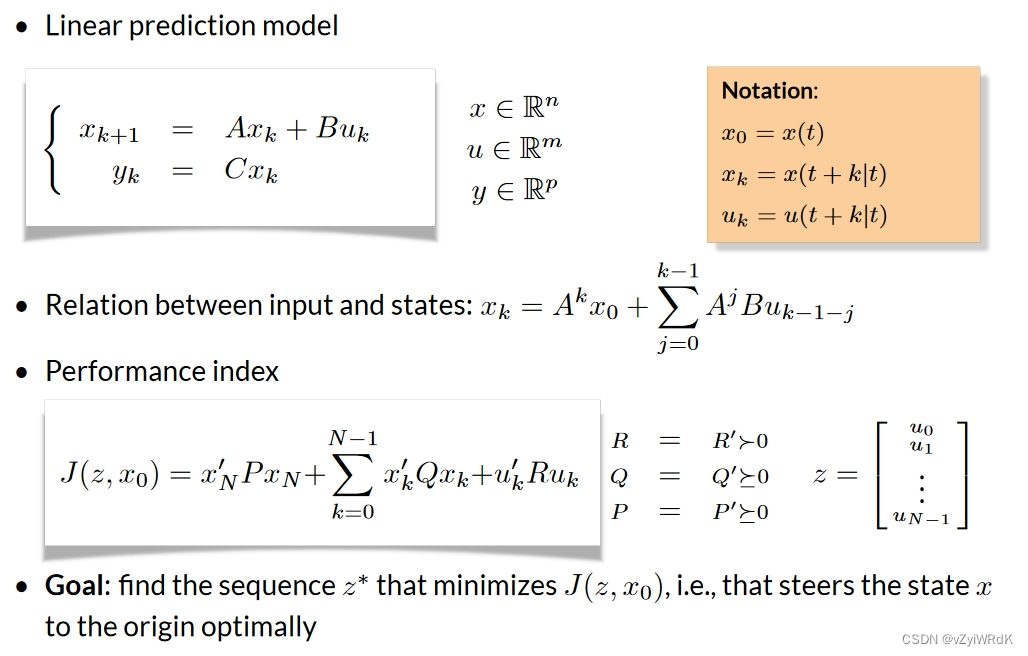
MPC将系统建模为一个多变量动态系统，可以使用常见的状态空间法来建立模型。在建立模型时，需要考虑系统的变量、输入、输出、约束条件等因素，并确定系统的状态向量和输入向量，以及它们之间的关系。模型建立完成后，需要在系统的当前状态下进行预测，并得到一个未来一段时间内的状态序列和输入序列。

1. 优化问题建立

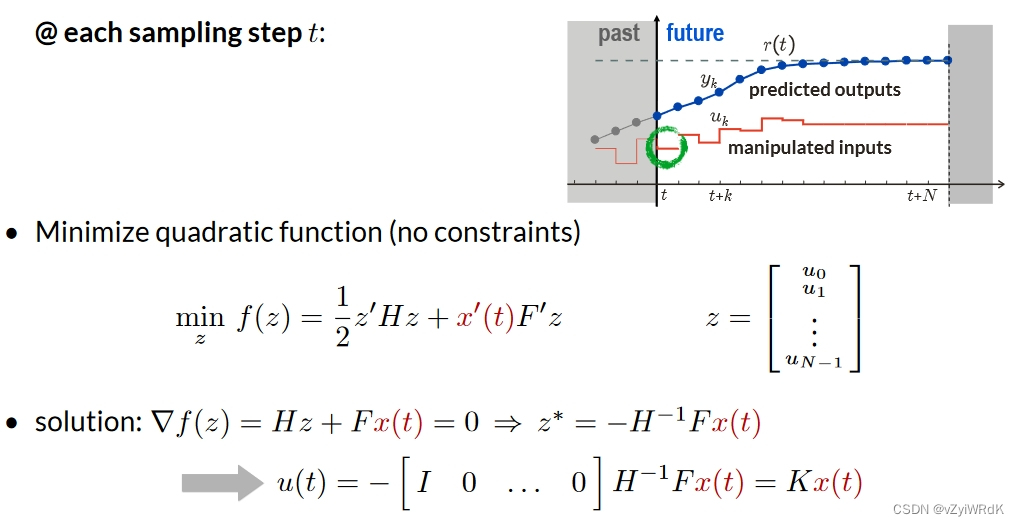
在得到未来一段时间内的状态序列和输入序列之后，MPC将控制问题转化为一个优化问题。该问题的目标是寻找符合系统约束条件的最优控制输入序列，使得预测时间内的系统状态能够尽量接近于期望的轨迹。优化问题通常可以表示为如下的数学形式：

minimize J = Ψ(x(N)) + ∑i=0~N-1 L(x(i),u(i)) subject to x(0) = x(t) x(i+1) = f(x(i),u(i)) i=0,1,...,N-1 u(i) ∈ U(i)

其中，N表示预测的时间步数，x表示系统状态，u表示控制输入，Ψ(x(N))表示终端状态的代价函数，L(x(i),u(i))表示中间状态的代价函数，f(x(i),u(i))表示系统的动力学模型，U(i)表示输入约束。

1. 控制指令计算

通过求解上述的优化问题，即可得到未来一段时间内的最优控制输入序列。对于当前时刻，MPC将该最优控制输入序列的第一个元素作为当前时刻的控制指令。

二、Matlab和C++两种编程实现

MPC控制器的实现通常可以使用Matlab或C++来进行编程。这里我们将针对这两种编程语言，分别介绍MPC的实现方法。

1. Matlab实现

Matlab是一种常用的科学计算软件，它可以方便地进行矩阵运算和优化求解。因此，在MPC控制器的实现中，Matlab通常被用来进行控制器的建模、仿真和优化求解。

具体来说，在Matlab中实现MPC控制器可以遵循以下步骤：

1. 建立系统动态模型，包括状态空间方程和成本函数。

2. 设定MPC的参数，包括预测时间步数、控制器权重矩阵、控制输入限制等。

3. 进行优化求解，并得到当前时刻的最优控制指令。

4. 将最优控制指令作为输入引入系统，计算系统的下一个状态。

5. 重复执行2)~4)步骤，直至控制任务完成。

1. C++实现

C++是一种高效的编程语言，具有快速执行和优秀的内存管理能力。因此，在需要实时控制的场景下，通常会使用C++来实现MPC控制器。

具体来说，在C++中实现MPC控制器可以遵循以下步骤：

1. 建立系统动态模型和成本函数，可以采用离散化方法来将连续时间动态方程转化为离散时间方程。

2. 设定MPC的参数，包括预测时间步数、控制器权重矩阵、控制输入限制等。

3. 利用优化库（如qpOASES）求解优化问题，并得到当前时刻的最优控制指令。

4. 将最优控制指令作为输入引入系统，计算系统的下一个状态。

5. 重复执行2)~4)步骤，直至控制任务完成。

三、四个实际控制工程案例

为了演示MPC模型预测控制的应用，我们提供了四个实际控制工程案例，分别是双积分控制系统、倒立摆控制系统、车辆运动学跟踪控制系统和车辆动力学跟踪控制系统。在这些案例中，我们将会根据实际应用需求来演示MPC模型预测控制的实现方法，并提供相应的文档和代码。

1. 双积分控制系统

双积分控制系统是一种常见的高精度控制系统，可以用于控制机器人的位置和速度等。在该案例中，我们将使用MPC模型预测控制来实现对双积分控制系统的控制。具体来说，我们将建立系统的动态模型和成本函数，并使用Matlab和C++两种编程语言来实现MPC控制器。最终，我们将会演示如何使用MPC控制器来控制双积分系统的位置和速度。

1. 倒立摆控制系统

倒立摆控制系统是一种典型的非线性系统，在控制领域中被广泛应用。在该案例中，我们将使用MPC模型预测控制来实现对倒立摆控制系统的控制。具体来说，我们将建立系统的动态模型和成本函数，并使用Matlab和C++两种编程语言来实现MPC控制器。最终，我们将会演示如何使用MPC控制器来控制倒立摆系统的倾斜角度。

1. 车辆运动学跟踪控制系统

车辆运动学跟踪控制系统是一种常见的车辆控制系统，可以用于控制车辆的位置和速度等。在该案例中，我们将使用MPC模型预

相关代码,程序地址：http://lanzouw.top/655344134433.html