如何通俗理解EM算法
前言
了解过EM算法的同学可能知道,EM算法是数据挖掘十大算法,可谓搞机器学习或数据挖掘的基本绕不开,但EM算法又像数据结构里的KMP算法,看似简单但又貌似不是一看就懂,想绕开却绕不开的又爱又恨,可能正在阅读此文的你感同身受。
一直以来,我都坚持一个观点:当你学习某个知识点感觉学不懂时,十有八九不是你不够聪明,十有八九是你所看的资料不够通俗、不够易懂(如果还是不行,问人)。
写本EM笔记之前,翻阅了很多资料,有比较通俗的,但大部分都不太好懂,本文力争通俗易懂且完整全面,包括原理、推导、应用,目标是即便其他所有EM文章你都没看懂,那本文也要让你看懂。
故本文会先少谈公式多举例,等明白了EM算法的本质和意义之后,再细究公式则水到渠成。有何问题,欢迎随时留言评论,thanks。
一 什么是极大似然
到底什么是EM算法呢?Wikipedia给的解释是:
最大期望算法(Expectation-maximization algorithm,又译为期望最大化算法),是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。
最大期望算法经过两个步骤交替进行计算,
- 第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;
- 第二步是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
1.1 似然函数
你懂了么?十有八九你没懂。因为你可能不懂什么是最大似然估计?而想了解最大似然估计,又得先从似然函数开始。但什么又是似然函数
在数理统计学中,似然函数是一种关于统计模型中的参数的函数,表示模型参数中的似然性。“似然性”与“或然性”或“概率”意思相近,都是指某种事件发生的可能性。
而极大似然就相当于最大可能的意思。
比如你一位同学和一位猎人一起外出打猎,一只野兔从前方窜过。只听一声枪响,野兔应声到下,如果要你推测,这一发命中的子弹是谁打的?你就会想,只发一枪便打中,由于猎人命中的概率一般大于你那位同学命中的概率,从而推断出这一枪应该是猎人射中的。
这个例子所作的推断就体现了最大似然法的基本思想。
多数情况下我们是根据已知条件来推算结果,而最大似然估计是已经知道了结果,然后寻求使该结果出现的可能性最大的条件,以此作为估计值。
看到没,概率是根据条件推测结果,而似然则是根据结果反推条件。在这种意义上,似然函数可以理解为条件概率的逆反。
假定已知某个参数B时,推测事件A会发生的概率写作:

通过贝叶斯公式,可以得出

现在我们反过来:事件A发生已经了,请通过似然函数![]() ,估计参数B的可能性。
,估计参数B的可能性。
一上公式,你可能就懵圈了。然后回想起我前沿开头所说的话:难道就没有一篇通俗易懂的么?
答案,当然是有的。我们从一个具体的例子人手。
1.2 似然函数举例:已知样本X,求参数θ
自从Google的围棋机器人AlphaGo通过4:1战胜人类世界冠军李世石之后,人工智能的大潮便一发不可收拾,在无人驾驶、人脸识别、安防监控、医疗影像等各领域大行其道。而专注AI教育的七月在线也已于2017年年底累积了10万AI学员。
假定我们需要统计七月在线10万学员中男生女生的身高分布,怎么统计呢?考虑到10万的数量巨大,所以不可能一个一个的去统计。对的,随机抽样,从10万学员中随机抽取100个男生,100个女生,然后依次统计他们各自的身高。
对于这个问题,我们通过数学建模抽象整理下
- 首先我们从10万学员中抽取到100个男生/女生的身高,组成样本集X,X={x1,x2,…,xN},其中xi表示抽到的第i个人的身高,N等于100,表示抽到的样本个数。
- 假定男生的身高服从正态分布
 ,女生的身高则服从另一个正态分布:
,女生的身高则服从另一个正态分布:  。
。 - 但是这两个分布的均值u和方差∂2都不知道(别问我,均值是啥,方差又是啥,请查Google或Wikipedia),设为未知参数θ=[u, ∂]T
- 现在需要用极大似然法(MLE),通过这100个男生或100个女生的身高结果,即样本集X来估计两个正态分布的未知参数θ,问题定义相当于已知X,求θ,换言之就是求p(θ|x)
因为这些男生(的身高)是服从同一个高斯分布p(x|θ)的。那么抽到男生A(的身高)的概率是p(xA|θ),抽到男生B的概率是p(xB|θ),考虑到他们是独立的,所以同时抽到男生A和男生B的概率是p(xA|θ)* p(xB|θ)。
同理,我从分布是p(x|θ)的总体样本中同时抽到这100个男生样本的概率,也就是样本集X中100个样本的联合概率(即它们各自概率的乘积),用下式表示:

插一句,有个文章中会用这个表示p(x|θ),有的文章会用p(x;θ),不过,不管用哪种表示方法,本质都是一样的。当然,如果涉及到Bayes公式的话,用前者表示p(x|θ)更好。
在七月在线那么多男学员中,我一抽就抽到这100个男生,而不是其他人,那说明在整个学校中,这100个人(的身高)出现的概率最大啊,这个概率就是上面这个似然函数L(θ),怎么做到的呢?换言之,怎样的θ能让L(θ)最大?
1.3 极大似然即最大可能
假定我们找到一个参数 ,能使似然函数L(θ)最大(也就是说抽到这100个男生的身高概率最大),则
,能使似然函数L(θ)最大(也就是说抽到这100个男生的身高概率最大),则 应该是“最可能”的参数值,相当于θ的极大似然估计量。记为:
应该是“最可能”的参数值,相当于θ的极大似然估计量。记为:

这里的L(θ)是连乘的,为了便于分析,我们可以定义对数似然函数,将其变成连加的:

现在需要使θ的似然函数L(θ)极大化,然后极大值对应的θ就是我们的估计。
对于求一个函数的极值,通过我们在本科所学的微积分知识,最直接的设想是求导,然后让导数为0,那么解这个方程得到的θ就是了(当然,前提是函数L(θ)连续可微)。但,如果θ是包含多个参数的向量那怎么处理呢?当然是求L(θ)对所有参数的偏导数,也就是梯度了,从而n个未知的参数,就有n个方程,方程组的解就是似然函数的极值点了,最终得到这n个参数的值。
求极大似然函数估计值的一般步骤:
- 写出似然函数;
- 对似然函数取对数,并整理;
- 求导数,令导数为0,得到似然方程;
- 解似然方程,得到的参数即为所求;
二、EM算法的通俗理解
2.1 极大似然估计的复杂情形
我们已经知道,极大似然估计用一句话概括就是:知道结果,反推条件θ。
例如,在上文中,为了统计七月在线10万学员中男生女生的身高分布
- 首先我们从10万学员中抽取到100个男生/女生的身高,组成样本集X,X={x1,x2,…,xN},其中xi表示抽到的第i个人的身高,N等于100,表示抽到的样本个数。
- 假定男生的身高服从正态分布
,女生的身高则服从另一个正态分布:
,但是这两个分布的均值u和方差∂2都不知道,设为未知参数θ=[u, ∂]T
- 现在需要用极大似然法(MLE),通过这100个男生或100个女生的身高结果,即样本集X来估计两个正态分布的未知参数θ,问题定义相当于已知X,求θ,换言之就是求p(θ|x)
极大似然估计的目标是求解实现结果的最佳参数θ,但极大似然估计需要面临的概率分布只有一个或者知道结果是通过哪个概率分布实现的,只不过你不知道这个概率分布的参数。
但现在我们让情况复杂一点,比如这100个男生和100个女生混在一起了。我们拥有200个人的身高数据,却不知道这200个人每一个是男生还是女生,此时的男女性别就像一个隐变量。
这时候情况就有点尴尬,因为通常来说,我们只有知道了精确的男女身高的正态分布参数我们才能知道每一个人更有可能是男生还是女生。反过来,我们只有知道了每个人是男生还是女生才能尽可能准确地估计男女各自身高的正态分布的参数。
而EM算法就是为了解决“极大似然估计”这种更复杂而存在的。
2.2 EM算法中的隐变量
理解EM算法中的隐变量很关键,就如理解KMP那必须得理解NEXT数组的意义一样。
一般的用Y表示观测到的随机变量的数据,Z表示隐随机变量的数据(因为我们观测不到结果是从哪个概率分布中得出的,所以将这个叫做隐变量)。于是Y和Z连在一起被称为完全数据,仅Y一个被称为不完全数据。
这时有没有发现EM算法面临的问题主要就是:有个隐变量数据Z。而如果Z已知的话,那问题就可用极大似然估计求解了。 于是乎,怎么把Z变成已知的?
再举第二个日常生活的例子。
假定你是一五星级酒店的厨师,现在需要把锅里的菜平均分配到两个碟子里。如果只有一个碟子乘菜那就什么都不用说了,但问题是有2个碟子,正因为根本无法估计一个碟子里应该乘多少菜,所以无法一次性把菜完全平均分配。
解法:
- 大厨先把锅里的菜一股脑倒进两个碟子里,然后看看哪个碟子里的菜多,就把这个碟子中的菜往另一个碟子中匀匀,之后重复多次匀匀的过程,直到两个碟子中菜的量大致一样。 上面的例子中,平均分配这个结果是“观测数据z”,为实现平均分配而给每个盘子分配多少菜是“待求参数θ”,分配菜的手感就是“概率分布”。
- 于是若只有一个盘子,那概率分布就确定了(“把锅里的菜全部倒到一个盘子”这样的手感是个人都有吧),而因为有两个盘子,所以“给一个盘子到多少菜才好”的手感就有些模糊不定,不过我们可以采用上面的解法来实现最终目标。
EM算法的思想就是:
- 给θ自主规定个初值(既然我不知道想实现“两个碟子平均分配锅里的菜”的话每个碟子需要有多少菜,那我就先估计个值);
- 根据给定观测数据和当前的参数θ,求未观测数据z的条件概率分布的期望(在上一步中,已经根据手感将菜倒进了两个碟子,然后这一步根据“两个碟子里都有菜”和“当前两个碟子都有多少菜”来判断自己倒菜的手感);
- 上一步中z已经求出来了,于是根据极大似然估计求最优的θ’(手感已经有了,那就根据手感判断下盘子里应该有多少菜,然后把菜匀匀);
- 因为第二步和第三步的结果可能不是最优的,所以重复第二步和第三步,直到收敛(重复多次匀匀的过程,直到两个碟子中菜的量大致一样)。
而上面的第二步被称作E步(求期望),第三步被称作M步(求极大化),从而不断的E、M。
2.3 EM算法的第三个例子:抛硬币
Nature Biotech在他的一篇EM tutorial文章《Do, C. B., & Batzoglou, S. (2008). What is the expectation maximization algorithm?. Nature biotechnology, 26(8), 897.》中,用了一个投硬币的例子来讲EM算法的思想。
比如两枚硬币A和B,如果知道每次抛的是A还是B,那可以直接估计(见下图a)。
如果不知道抛的是A还是B(这时就刺激了吧,对的,这就是咱们不知情的隐变量),只观测到5轮循环每轮循环10次,共计50次投币的结果,这时就没法直接估计A和B的正面概率。这时,就轮到EM算法出场了(见下图b)。
可能咋一看,你没看懂。没关系,我们来通俗化这个例子。
还是两枚硬币A和B,假定随机抛掷后正面朝上概率分别为PA,PB。为了估计这两个硬币朝上的概率,咱们轮流抛硬币A和B,每一轮都连续抛5次,总共5轮:
| 硬币 | 结果 | 统计 |
|---|---|---|
| A | 正正反正反 | 3正-2反 |
| B | 反反正正反 | 2正-3反 |
| A | 正反反反反 | 1正-4反 |
| B | 正反反正正 | 3正-2反 |
| A | 反正正反反 | 2正-3反 |
硬币A被抛了15次,在第一轮、第三轮、第五轮分别出现了3次正、1次正、2次正,所以很容易估计出PA,类似的,PB也很容易计算出来,如下:
PA = (3+1+2)/ 15 = 0.4
PB= (2+3)/10 = 0.5
问题来了,如果我们不知道抛的硬币是A还是B呢(即硬币种类是隐变量),然后再轮流抛五轮,得到如下结果:
| 硬币 | 结果 | 统计 |
|---|---|---|
| Unknown | 正正反正反 | 3正-2反 |
| Unknown | 反反正正反 | 2正-3反 |
| Unknown | 正反反反反 | 1正-4反 |
| Unknown | 正反反正正 | 3正-2反 |
| Unknown | 反正正反反 | 2正-3反 |
OK,问题变得有意思了。现在我们的目标没变,还是估计PA和PB,需要怎么做呢?
显然,此时我们多了一个硬币种类的隐变量,设为z,可以把它认为是一个5维的向量(z1,z2,z3,z4,z5),代表每次投掷时所使用的硬币,比如z1,就代表第一轮投掷时使用的硬币是A还是B。
- 但是,这个变量z不知道,就无法去估计PA和PB,所以,我们必须先估计出z,然后才能进一步估计PA和PB。
- 可要估计z,我们又得知道PA和PB,这样我们才能用极大似然概率法则去估计z,这不是鸡生蛋和蛋生鸡的问题吗,如何破?
答案就是先随机初始化一个PA和PB,用它来估计z,然后基于z,还是按照最大似然概率法则去估计新的PA和PB,如果新的PA和PB和我们初始化的PA和PB一样,请问这说明了什么?
这说明我们初始化的PA和PB是一个相当靠谱的估计!
就是说,我们初始化的PA和PB,按照最大似然概率就可以估计出z,然后基于z,按照最大似然概率可以反过来估计出P1和P2,当与我们初始化的PA和PB一样时,说明是P1和P2很有可能就是真实的值。这里面包含了两个交互的最大似然估计。
如果新估计出来的PA和PB和我们初始化的值差别很大,怎么办呢?就是继续用新的P1和P2迭代,直至收敛。
我们不妨这样,先随便给PA和PB赋一个值,比如:
硬币A正面朝上的概率PA = 0.2
硬币B正面朝上的概率PB = 0.7
然后,我们看看第一轮抛掷最可能是哪个硬币。
如果是硬币A,得出3正2反的概率为 0.2*0.2*0.2*0.8*0.8 = 0.00512
如果是硬币B,得出3正2反的概率为0.7*0.7*0.7*0.3*0.3=0.03087
然后依次求出其他4轮中的相应概率。做成表格如下(标粗表示其概率更大):
| 轮数 | 若是硬币A | 若是硬币B |
|---|---|---|
| 1 | 0.00512,即0.2 0.2 0.2 0.8 0.8,3正-2反 | 0.03087,3正-2反 |
| 2 | 0.02048,即0.2 0.2 0.8 0.8 0.8,2正-3反 | 0.01323,2正-3反 |
| 3 | 0.08192,即0.2 0.8 0.8 0.8 0.8,1正-4反 | 0.00567,1正-4反 |
| 4 | 0.00512,即0.2 0.2 0.2 0.8 0.8,3正-2反 | 0.03087,3正-2反 |
| 5 | 0.02048,即0.2 0.2 0.8 0.8 0.8,2正-3反 | 0.01323,2正-3反 |
按照最大似然法则:
第1轮中最有可能的是硬币B
第2轮中最有可能的是硬币A
第3轮中最有可能的是硬币A
第4轮中最有可能的是硬币B
第5轮中最有可能的是硬币A
我们就把概率更大,即更可能是A的,即第2轮、第3轮、第5轮出现正的次数2、1、2相加,除以A被抛的总次数15(A抛了三轮,每轮5次),作为z的估计值,B的计算方法类似。然后我们便可以按照最大似然概率法则来估计新的PA和PB。
PA = (2+1+2)/15 = 0.33
PB =(3+3)/10 = 0.6
设想我们是全知的神,知道每轮抛掷时的硬币就是如本文本节开头标示的那样,那么,PA和PB的最大似然估计就是0.4和0.5(下文中将这两个值称为PA和PB的真实值)。那么对比下我们初始化的PA和PB和新估计出的PA和PB:
| 初始化的PA | 估计出的PA | 真实的PA | 初始化的PB | 估计出的PB | 真实的PB |
|---|---|---|---|---|---|
| 0.2 | 0.33 | 0.4 | 0.7 | 0.6 | 0.5 |
看到没?我们估计的PA和PB相比于它们的初始值,更接近它们的真实值了!就这样,不断迭代 不断接近真实值,这就是EM算法的奇妙之处。
可以期待,我们继续按照上面的思路,用估计出的PA和PB再来估计z,再用z来估计新的PA和PB,反复迭代下去,就可以最终得到PA = 0.4,PB=0.5,此时无论怎样迭代,PA和PB的值都会保持0.4和0.5不变,于是乎,我们就找到了PA和PB的最大似然估计。
三、EM算法的公式推导
3.1 EM算法的目标函数
还记得1.2节开头所说的吧?
从分布是p(x|θ)的总体样本中抽取到这100个样本的概率,也就是样本集X中各个样本的联合概率,用下式表示:
假设我们有一个样本集{x(1),…,x(m)},包含m个独立的样本,现在我们想找到每个样本隐含的类别z,能使得p(x,z)最大。p(x,z)的极大似然估计如下:

第一步是对极大似然取对数,第二步是对每个样例的每个可能类别z求联合分布概率和。但是直接求一般比较困难,因为有隐藏变量z存在,但是一般确定了z后,求解就容易了。
对于参数估计,我们本质上还是想获得一个使似然函数最大化的那个参数θ,现在与极大似然不同的只是似然函数式中多了一个未知的变量z,见下式(1)。也就是说我们的目标是找到适合的θ和z,以让L(θ)最大。那我们也许会想,你就是多了一个未知的变量而已啊,我也可以分别对未知的θ和z分别求偏导,再令其等于0,求解出来不也一样吗?

本质上我们是需要最大化(1)式,也就是似然函数,但是可以看到里面有“和的对数”,求导后形式会非常复杂(自己可以想象下log(f1(x)+ f2(x)+ f3(x)+…)复合函数的求导),所以很难求解得到未知参数z和θ。
我们把分子分母同乘以一个相等的函数(即隐变量Z的概率分布Qi(z(i)),其概率之和等于1,即 ),即得到上图中的(2)式,但(2)式还是有“和的对数”,还是求解不了,咋办呢?接下来,便是见证神奇的时刻,我们通过Jensen不等式可得到(3)式,此时(3)式变成了“对数的和”,如此求导就容易了。
),即得到上图中的(2)式,但(2)式还是有“和的对数”,还是求解不了,咋办呢?接下来,便是见证神奇的时刻,我们通过Jensen不等式可得到(3)式,此时(3)式变成了“对数的和”,如此求导就容易了。
从(2)式到(3)式,神奇的地方有两点:
- 当我们在求(2)式的极大值时,(2)式不太好计算,我们便想(2)式大于某个方便计算的下界(3)式,而我们尽可能让下界(3)式最大化,直到(3)式的计算结果等于(2)式,便也就间接求得了(2)式的极大值;
- Jensen不等式,促进神奇发生的Jensen不等式到底是什么来历呢?
3.2 Jensen不等式
设f是定义域为实数的函数
- 如果对于所有的实数x,f(x)的二次导数
 ,那么f是凸函数。
,那么f是凸函数。 - 当x是向量时,如果其hessian矩阵H是半正定的(
 ),那么f是凸函数。
),那么f是凸函数。 - 如果
 或者
或者 ,那么称f是严格凸函数。
,那么称f是严格凸函数。
Jensen不等式表述如下:
如果f是凸函数,X是随机变量,那么:E[f(X)]>=f(E[X]),通俗的说法是函数的期望大于等于期望的函数。
特别地,如果f是严格凸函数,当且仅当P(X = EX) = 1,即X是常量时,上式取等号,即E[f(X)] = f(EX)。
如下图所示

图中,实线f是凸函数(因为函数上方的区域是一个凸集),X是随机变量,有0.5的概率是a,有0.5的概率是b(就像抛硬币一样)。X的期望值就是a和b的中值了,可以很明显从看出,![clip_image010[1]](https://i-blog.csdnimg.cn/blog_migrate/e97f1d1833d0ccf09e6ab51ef18afedf.png) 。
。
当然,当f是(严格)凹函数当且仅当-f是(严格)凸函数,不等号方向反向,也就是 。
。
回到公式(2),因为f(x)=log x为凹函数(其二次导数为-1/x2<0)。
(2)式中 就是
就是  的期望。为什么?回想期望公式中的Lazy Statistician规则,如下
的期望。为什么?回想期望公式中的Lazy Statistician规则,如下
| 设Y是随机变量X的函数 (1) X是离散型随机变量,它的分布律为 (2) X是连续型随机变量,它的概率密度为 |
考虑到E(X)=∑x*p(x),f(X)是X的函数,则E(f(X))=∑f(x)*p(x)),又 ,所以就可以得到公式(3)的不等式了:
,所以就可以得到公式(3)的不等式了:

OK,到这里,现在式(3)就容易地求导了,但是式(2)和式(3)是不等号啊,式(2)的最大值不是式(3)的最大值啊,而我们想得到式(2)的最大值,那怎么办呢?
上面的式(2)和式(3)不等式可以写成:似然函数L(θ)>=J(z,Q),如3.1节最后所说,我们可以通过不断的最大化这个下界J,来使得L(θ)不断提高,最终达到L(θ)的最大值。
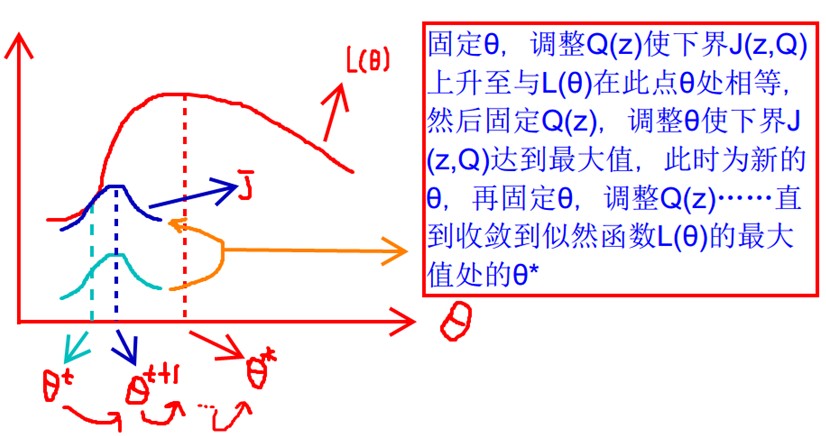
见上图,我们固定θ,调整Q(z)使下界J(z,Q)上升至与L(θ)在此点θ处相等(绿色曲线到蓝色曲线),然后固定Q(z),调整θ使下界J(z,Q)达到最大值(θt到θt+1),然后再固定θ,调整Q(z)……直到收敛到似然函数L(θ)的最大值处的θ*。
这里有两个问题:
- 什么时候下界J(z,Q)与L(θ)在此点θ处相等?
- 为什么一定会收敛?
首先第一个问题,在Jensen不等式中说到,当自变量X是常数的时候,等式成立。换言之,为了让(3)式取等号,我们需要:

其中,c为常数,不依赖于 。对该式做个变换,并对所有的z求和,得到
。对该式做个变换,并对所有的z求和,得到

因为前面提到 (对的,隐变量Z的概率分布,其概率之和等于1),所以可以推导出:
(对的,隐变量Z的概率分布,其概率之和等于1),所以可以推导出:
![]()
所以通过 ,可求得
,可求得![]() 的值(即
的值(即![]() /c),加之
/c),加之![]() ,所以
,所以![]() 为
为

瞬间豁然开朗!至此,我们推出了在固定参数θ后,使下界拉升的Q(z)的计算公式就是条件概率,解决了Q(z)如何选择的问题。这一步就是E步,建立L(θ)的下界。
接下来的M步,就是在给定Q(z)后,调整θ,去极大化L(θ)的下界J(z,Q),毕竟在固定Q(z)后,下界还可以调整的更大。
这就是EM算法的步骤。
3.3 EM算法的流程及证明
我们来总结下,期望最大EM算法是一种从不完全数据或有数据丢失的数据集(存在隐含变量)中求解概率模型参数的最大似然估计方法。
换言之,当我们不知道隐变量z的具体取值时(比如是硬币A还是硬币B),也就不好判断硬币A或硬币B正面朝上的概率θ,既然这样,那就
| 1 随机初始化分布参数θ 2 然后循环重复直到收敛 { (E步,求Q函数)对于每一个i,计算根据上一次迭代的模型参数来计算出隐性变量的后验概率(其实就是隐性变量的期望),来作为隐藏变量的现估计值: (M步,求使Q函数获得极大时的参数取值)将似然函数最大化以获得新的参数值 |
就这样,Q(z)求出来代入到θ,θ求出来又反代回Q(z),如此不断的迭代,就可以得到使似然函数L(θ)最大化的参数θ了。
还有就是,如上节所提出的第二个问题,它会收敛吗?或者,如何怎么确保EM收敛?
这里,直接引用JerryLead做的机器学习笔记证明下,我做了相关注解、解释。
假定
和
是EM第 t 次和 t+1 次迭代后的结果(对的,上标 t 表示第 t 次迭代)。如果我们证明了
,也就是说极大似然估计单调增加,那么最终我们会到达最大似然估计的最大值。
下面来证明。
选定
后,我们得到E步
这一步保证了在给定
时,Jensen不等式中的等式成立,也就是
然后进行M步,固定
,并将
视作变量,对上面的
求导后,得到
,这样经过一些推导会有以下式子成立:
解释下第(4)步,得到
时,只是最大化
,也就是
的下界,而没有使等式成立,等式成立只有是在固定
,并按E步得到
时才能成立。
况且根据我们前面得到的下式,对于所有的
和
都成立

第(5)步利用了M步的定义,M步就是将
调整到
,使得下界最大化。因此(5)成立,(6)是之前的等式结果。
这样就证明了
会单调增加。一种收敛方法是
不再变化,还有一种就是变化幅度很小。
再次解释一下(4)、(5)、(6)。
- 首先(4)对所有的参数都满足,而其等式成立条件只是在固定
![clip_image026[4]](https://i-blog.csdnimg.cn/blog_migrate/ed669dddfc3d64d5e79c7a89c6020539.png) ,并调整好Q时成立,而第(4)步只是固定Q,调整
,并调整好Q时成立,而第(4)步只是固定Q,调整![clip_image026[4]](https://i-blog.csdnimg.cn/blog_migrate/ed669dddfc3d64d5e79c7a89c6020539.png) ,不能保证等式一定成立。
,不能保证等式一定成立。 - (4)到(5)就是M步的定义,(5)到(6)是前面E步所保证等式成立条件。也就是说E步会将下界拉到与
 一个特定值(这里
一个特定值(这里![clip_image088[2]](https://i-blog.csdnimg.cn/blog_migrate/2ba9d18b34145b8f20bc067d6736aab8.png) )一样的高度,而此时发现下界仍然可以上升,因此经过M步后,下界又被拉升,但达不到与
)一样的高度,而此时发现下界仍然可以上升,因此经过M步后,下界又被拉升,但达不到与![clip_image102[2]](https://i-blog.csdnimg.cn/blog_migrate/7870a70932615d8c2e468f0a371dac33.png) 另外一个特定值一样的高度,之后E步又将下界拉到与这个特定值一样的高度,重复下去,直到最大值。
另外一个特定值一样的高度,之后E步又将下界拉到与这个特定值一样的高度,重复下去,直到最大值。
结束了?NO,M步中,到底如何求θ的极值呢?虽说求极值的方法有很多种,但本文还是要展开下。
首先,把Q(z)求出来代入到θ,可得:
 (7)
(7)
其中:
![]() (8)
(8)
 (9)
(9)
直接对![]() 求导还是很麻烦,不过已经可以用迭代来最大化啦。
求导还是很麻烦,不过已经可以用迭代来最大化啦。
- 先根据式(9),由
 求条件分布
求条件分布 
- 再把
 带入(7)中,得到
带入(7)中,得到
 (10)
(10)
这就只需要最大化联合分布 ![]() 了,最大化求出
了,最大化求出 ![]() 后再重复这2步。
后再重复这2步。
M步很显然,就是最大化那一步,E步又从何谈起呢?根据式(10)有

其实,E步就是求给定X下的条件期望,也就是后验期望,使得式(3)的琴生不等式能够取等号,是对Jensen不等式中,小的那一端进行放大,使其等于大的那一端,这是一次放大;M步最大化联合分布,通过0梯度,拉格朗日法等方法求极值点,又是一次放大。只要似然函数是有界的,只要M步中的0梯度点是极大值点,一直放大下去就能找到最终所求。
3.4 EM算法另一种理解
如果我们定义

从前面的推导中我们知道 ,EM可以看作是J的坐标上升法,E步固定
,EM可以看作是J的坐标上升法,E步固定![clip_image026[8]](https://i-blog.csdnimg.cn/blog_migrate/7b34a754c376e03868b757655e4229f4.png) ,优化
,优化 ,M步固定
,M步固定 优化
优化![clip_image026[9]](https://i-blog.csdnimg.cn/blog_migrate/4e6b5d08652e566b2447849c39907159.png) 。
。
坐标上升法(Coordinate ascent):

图中的直线式迭代优化的路径,可以看到每一步都会向最优值前进一步,而且前进路线是平行于坐标轴的,因为每一步只优化一个变量。
这犹如在x-y坐标系中找一个曲线的极值,然而曲线函数不能直接求导,因此什么梯度下降方法就不适用了。但固定一个变量后,另外一个可以通过求导得到,因此可以使用坐标上升法,一次固定一个变量,对另外的求极值,最后逐步逼近极值。
对应到EM上,就是:E步:固定θ,优化Q;M步:固定Q,优化θ;交替将极值推向最大。
四、EM应用:估计pLSA的两未知参数
关于EM算法的应用其实很多,最广泛的就是GMM混合高斯模型、聚类、HMM等等。比如聚类

本文重点讲下用EM算法估计主题模型pLSA的两未知参数。
4.1 pLSA模型下生成文档
一篇文章往往有多个主题,只是这多个主题各自在文档中出现的概率大小不一样。比如介绍一个国家的文档中,往往会分别从教育、经济、交通等多个主题进行介绍。那么在pLSA中,文档是怎样被生成的呢?
假设你要写M篇文档,由于一篇文档由各个不同的词组成,所以你需要确定每篇文档里每个位置上的词。
再假定你一共有K个可选的主题,有V个可选的词,咱们来玩一个扔骰子的游戏。
- 1. 假设你每写一篇文档会制作一颗K面的“文档-主题”骰子(扔此骰子能得到K个主题中的任意一个),和K个V面的“主题-词项” 骰子(每个骰子对应一个主题,K个骰子对应之前的K个主题,且骰子的每一面对应要选择的词项,V个面对应着V个可选的词)。
- 比如可令K=3,即制作1个含有3个主题的“文档-主题”骰子,这3个主题可以是:教育、经济、交通。然后令V = 3,制作3个有着3面的“主题-词项”骰子,其中,教育主题骰子的3个面上的词可以是:大学、老师、课程,经济主题骰子的3个面上的词可以是:市场、企业、金融,交通主题骰子的3个面上的词可以是:高铁、汽车、飞机。

- 比如可令K=3,即制作1个含有3个主题的“文档-主题”骰子,这3个主题可以是:教育、经济、交通。然后令V = 3,制作3个有着3面的“主题-词项”骰子,其中,教育主题骰子的3个面上的词可以是:大学、老师、课程,经济主题骰子的3个面上的词可以是:市场、企业、金融,交通主题骰子的3个面上的词可以是:高铁、汽车、飞机。
- 2. 每写一个词,先扔该“文档-主题”骰子选择主题,得到主题的结果后,使用和主题结果对应的那颗“主题-词项”骰子,扔该骰子选择要写的词。
- 先扔“文档-主题”的骰子,假设(以一定的概率)得到的主题是教育,所以下一步便是扔教育主题筛子,(以一定的概率)得到教育主题筛子对应的某个词:大学。
- 上面这个投骰子产生词的过程简化下便是:“先以一定的概率选取主题,再以一定的概率选取词”。事实上,一开始可供选择的主题有3个:教育、经济、交通,那为何偏偏选取教育这个主题呢?其实是随机选取的,只是这个随机遵循一定的概率分布。比如可能选取教育主题的概率是0.5,选取经济主题的概率是0.3,选取交通主题的概率是0.2,那么这3个主题的概率分布便是{教育:0.5,经济:0.3,交通:0.2},我们把各个主题z在文档d中出现的概率分布称之为主题分布,且是一个多项分布。
- 同样的,从主题分布中随机抽取出教育主题后,依然面对着3个词:大学、老师、课程,这3个词都可能被选中,但它们被选中的概率也是不一样的。比如大学这个词被选中的概率是0.5,老师这个词被选中的概率是0.3,课程被选中的概率是0.2,那么这3个词的概率分布便是{大学:0.5,老师:0.3,课程:0.2},我们把各个词语w在主题z下出现的概率分布称之为词分布,这个词分布也是一个多项分布。
- 所以,选主题和选词都是两个随机的过程,先从主题分布{教育:0.5,经济:0.3,交通:0.2}中抽取出主题:教育,然后从该教育主题对应的词分布{大学:0.5,老师:0.3,课程:0.2}中抽取出词:大学。
- 先扔“文档-主题”的骰子,假设(以一定的概率)得到的主题是教育,所以下一步便是扔教育主题筛子,(以一定的概率)得到教育主题筛子对应的某个词:大学。
- 3. 最后,你不停的重复扔“文档-主题”骰子和”主题-词项“骰子,重复N次(产生N个词),完成一篇文档,重复这产生一篇文档的方法M次,则完成M篇文档。
上述过程抽象出来即是pLSA的文档生成模型。在这个过程中,我们并未关注词和词之间的出现顺序,所以pLSA是一种词袋方法。具体说来,该模型假设一组共现(co-occurrence)词项关联着一个隐含的主题类别 。同时定义:
。同时定义:
 表示海量文档中某篇文档被选中的概率。
表示海量文档中某篇文档被选中的概率。 表示词
表示词 在给定文档
在给定文档 中出现的概率。
中出现的概率。
- 怎么计算得到呢?针对海量文档,对所有文档进行分词后,得到一个词汇列表,这样每篇文档就是一个词语的集合。对于每个词语,用它在文档中出现的次数除以文档中词语总的数目便是它在文档中出现的概率
 。
。
- 怎么计算得到呢?针对海量文档,对所有文档进行分词后,得到一个词汇列表,这样每篇文档就是一个词语的集合。对于每个词语,用它在文档中出现的次数除以文档中词语总的数目便是它在文档中出现的概率
 表示具体某个主题
表示具体某个主题 在给定文档
在给定文档 下出现的概率。
下出现的概率。 表示具体某个词
表示具体某个词 在给定主题
在给定主题 下出现的概率,与主题关系越密切的词,其条件概率
下出现的概率,与主题关系越密切的词,其条件概率 越大。
越大。
利用上述的第1、3、4个概率,我们便可以按照如下的步骤得到“文档-词项”的生成模型:
- 按照概率
 选择一篇文档
选择一篇文档
- 选定文档
 后,从主题分布中按照概率
后,从主题分布中按照概率 选择一个隐含的主题类别
选择一个隐含的主题类别
- 选定
 后,从词分布中按照概率
后,从词分布中按照概率 选择一个词
选择一个词
所以pLSA中生成文档的整个过程便是选定文档生成主题,确定主题生成词。
4.2 根据文档反推其主题分布
反过来,既然文档已经产生,那么如何根据已经产生好的文档反推其主题呢?这个利用看到的文档推断其隐藏的主题(分布)的过程(其实也就是产生文档的逆过程),便是主题建模的目的:自动地发现文档集中的主题(分布)。
换言之,人类根据文档生成模型写成了各类文章,然后丢给了计算机,相当于计算机看到的是一篇篇已经写好的文章。现在计算机需要根据一篇篇文章中看到的一系列词归纳出当篇文章的主题,进而得出各个主题各自不同的出现概率:主题分布。即文档d和单词w是可被观察到的,但主题z却是隐藏的。
如下图所示(图中被涂色的d、w表示可观测变量,未被涂色的z表示未知的隐变量,N表示一篇文档中总共N个单词,M表示M篇文档):
上图中,文档d和词w是我们得到的样本(样本随机,参数虽未知但固定,所以pLSA属于频率派思想。区别于参考文献8介绍的LDA中:样本固定,参数未知但不固定,是个随机变量,服从一定的分布,所以LDA属于贝叶斯派思想),可观测得到,所以对于任意一篇文档,其 是已知的。
是已知的。
从而可以根据大量已知的文档-词项信息 ,训练出文档-主题
,训练出文档-主题 和主题-词项
和主题-词项 ,如下公式所示:
,如下公式所示:
故得到文档中每个词的生成概率为:
由于 可事先计算求出,而
可事先计算求出,而 和
和 未知,所以
未知,所以 就是我们要估计的参数(值),通俗点说,就是要最大化这个θ。
就是我们要估计的参数(值),通俗点说,就是要最大化这个θ。
用什么方法进行估计呢,常用的参数估计方法有极大似然估计MLE、最大后验证估计MAP、贝叶斯估计等等。因为该待估计的参数中含有隐变量z,所以我们可以考虑EM算法。
4.3 EM算法估计pLSA的两未知参数
首先尝试从矩阵的角度来描述待估计的两个未知变量 和
和 。
。
- 假定用
 表示词表
表示词表 在主题
在主题 上的一个多项分布,则
上的一个多项分布,则 可以表示成一个向量,每个元素
可以表示成一个向量,每个元素 表示词项
表示词项 出现在主题
出现在主题 中的概率,即
中的概率,即
- 用
 表示所有主题
表示所有主题 在文档
在文档 上的一个多项分布,则
上的一个多项分布,则 可以表示成一个向量,每个元素
可以表示成一个向量,每个元素 表示主题
表示主题 出现在文档
出现在文档 中的概率,即
中的概率,即
这样,巧妙的把 和
和 转换成了两个矩阵。换言之,最终我们要求解的参数是这两个矩阵:
转换成了两个矩阵。换言之,最终我们要求解的参数是这两个矩阵:
由于词和词之间是相互独立的,所以整篇文档N个词的分布为:
再由于文档和文档之间也是相互独立的,所以整个语料库中词的分布为(整个语料库M篇文档,每篇文档N个词):
其中, 表示词项
表示词项 在文档
在文档 中的词频,
中的词频, 表示文档di中词的总数,显然有
表示文档di中词的总数,显然有 。
。
从而得到整个语料库的词分布的对数似然函数(下述公式中有个小错误,正确的应该是:N为M,M为N):
现在,我们需要最大化上述这个对数似然函数来求解参数 和
和 。对于这种含有隐变量的最大似然估计,可以使用EM算法。EM算法,分为两个步骤:先E-step,后M-step。
。对于这种含有隐变量的最大似然估计,可以使用EM算法。EM算法,分为两个步骤:先E-step,后M-step。
- E-step:假定参数已知,计算此时隐变量的后验概率。
利用贝叶斯法则,可以得到:
- M-step:带入隐变量的后验概率,最大化样本分布的对数似然函数,求解相应的参数。
观察之前得到的对数似然函数 的结果,由于文档长度
的结果,由于文档长度 可以单独计算,所以去掉它不影响最大化似然函数。此外,根据E-step的计算结果,把
可以单独计算,所以去掉它不影响最大化似然函数。此外,根据E-step的计算结果,把  代入
代入 ,于是我们只要最大化下面这个函数
,于是我们只要最大化下面这个函数  即可(下述公式中有个小错误,正确的应该是:N为M,M为N):
即可(下述公式中有个小错误,正确的应该是:N为M,M为N):
这是一个多元函数求极值问题,并且已知有如下约束条件(下述公式中有个小错误,正确的应该是:M为N):
熟悉凸优化的朋友应该知道,一般处理这种带有约束条件的极值问题,常用的方法便是拉格朗日乘数法,即通过引入拉格朗日乘子将约束条件和多元(目标)函数融合到一起,转化为无约束条件的极值问题。
这里我们引入两个拉格朗日乘子 和
和 ,从而写出拉格朗日函数(下述公式中有个小错误,正确的应该是:N为M,M为N):
,从而写出拉格朗日函数(下述公式中有个小错误,正确的应该是:N为M,M为N):
因为我们要求解的参数是 和
和 ,所以分别对
,所以分别对 和
和 求偏导,然后令偏导结果等于0,得到(下述公式中有个小错误,正确的应该是:N为M,M为N):
求偏导,然后令偏导结果等于0,得到(下述公式中有个小错误,正确的应该是:N为M,M为N):
消去拉格朗日乘子,最终可估计出参数 和
和 (下述公式中有个小错误,正确的应该是:N为M,M为N):
(下述公式中有个小错误,正确的应该是:N为M,M为N):
综上,在pLSA中:
- 由于
 和
和 未知,所以我们用EM算法去估计
未知,所以我们用EM算法去估计 这个参数的值。
这个参数的值。 - 而后,用
 表示词项
表示词项 出现在主题
出现在主题 中的概率,即
中的概率,即 ,用
,用 表示主题
表示主题 出现在文档
出现在文档 中的概率,即
中的概率,即 ,从而把
,从而把 转换成了“主题-词项”矩阵Φ(主题生成词),把
转换成了“主题-词项”矩阵Φ(主题生成词),把 转换成了“文档-主题”矩阵Θ(文档生成主题)。
转换成了“文档-主题”矩阵Θ(文档生成主题)。 - 最终求解出
 、
、 。
。
最后值得一提的是,在pLSA模型的基础上,加个贝叶斯框架,便是LDA,关于LDA的更多详情可以参看参考文献8。
五、参考文献与推荐阅读
- JerryLead:(EM算法)The EM Algorithm
- zouxy09:从最大似然到EM算法浅解
- 怎么通俗易懂地解释EM算法并且举个例子?
- milter:如何感性地理解EM算法?
- EM算法九层境界
- 七月在线公开课:18分钟EM算法
- 七月在线机器学习第九期第四次课:唐博士用5个小时详细剖析和推导EM算法
- 通俗理解LDA主题模型
六、后记
昨天白天谈合作,晚上在成都一家网吧 终于把EM算法笔记基本写完了,公式巨多 写通俗不易,所以费了比较大的劲,后面还得不断改改。
以下为修改的次数
- 8.25晚上,第一轮修改,完善隐变量z的概率密度函数Q(z)的计算公式就是条件概率那一块的推导;
- 8.26凌晨,第二轮修改,完善EM算法的公式推导,包括:Q(z)求出来代入到θ,θ求出来又反代回Q(z);
- 8.26上午,第三轮修改,完善EM算法中θ的迭代求解;
- 8.26晚上,第四轮修改,精简EM算法相关例子的描述,已让行文思路更清晰;
- 8.28上午,第五轮修改,增加EM算法估计pLSA的两未知参数,使得读者不但通晓本质、推导,而且熟练应用。
July、二零一八年八月。









 (g是连续函数),那么
(g是连续函数),那么 ,k=1,2,…。若
,k=1,2,…。若 绝对收敛,则有
绝对收敛,则有
 ,若
,若 绝对收敛,则有
绝对收敛,则有






































 600
600

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










