【梯度下降和正规方程】吴恩达机器学习笔记（四）

verse_armour

已于 2022-08-10 23:01:28 修改

阅读量586

点赞数 1

文章标签：机器学习线性回归回归

于 2022-08-10 19:59:55 首次发布

本文链接：https://blog.csdn.net/verse_armour/article/details/126084355

版权

吴恩达机器学习笔记（四）

文章目录

吴恩达机器学习笔记（四）

4-1.多功能(multiple features)

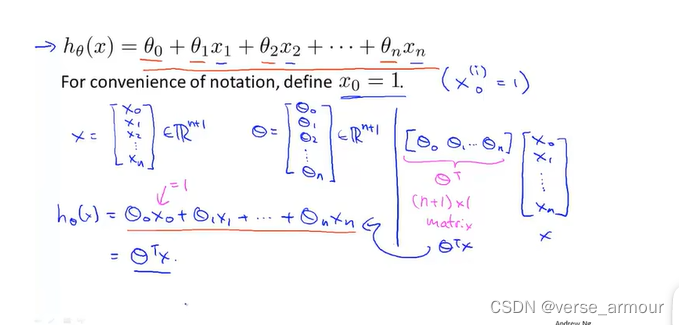
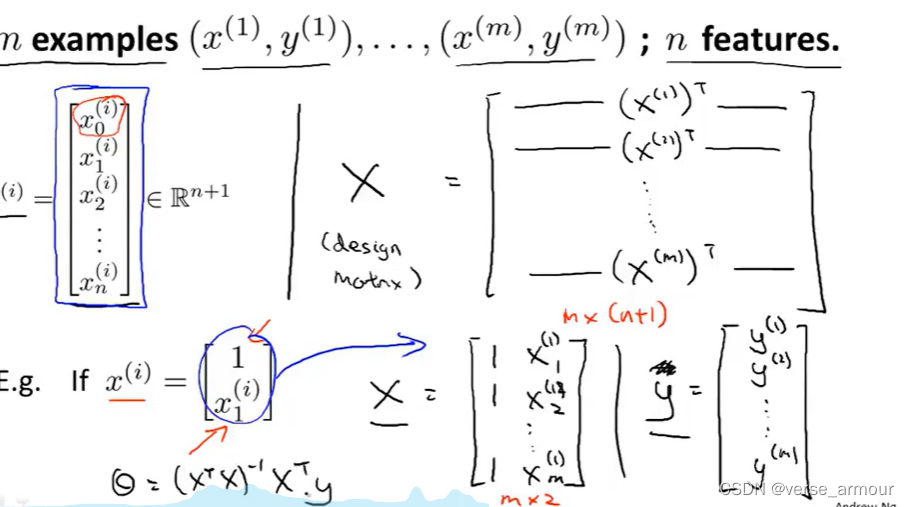
在这里插入图片描述

多元线性回归不妨定义 $x_0=1$ ，可以让多元线性回归的假设（预测）函数 （hypothesis function）
用矩阵的形式表达出来，结果更加紧凑。

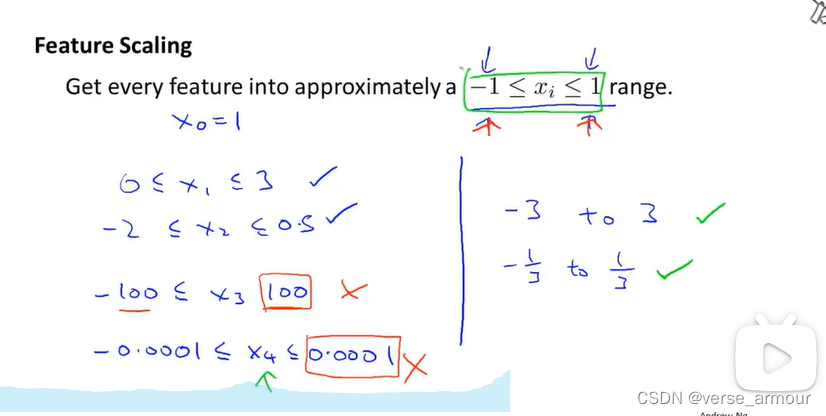
在这里插入图片描述

因此，总的来说，不用过于担心你的特征是否在完全相同的范围或区间内。但是只要它们足够接近（大概就是数量级保持一致）的话，梯度下降算法就会正常地工作。

4-2.多元梯度下降法

（1）数学原理

如何利用梯度下降法来处理多元线性回归
在这里插入图片描述

从一元线性回归到多元线性回归：每次迭代更新的参数变多，从2个参数到2个以上的参数。 $i$ 表示行：不同的样本； $j$ 表示列：不同的特征。

（2）多元梯度下降法——特征缩放（feature scaling）

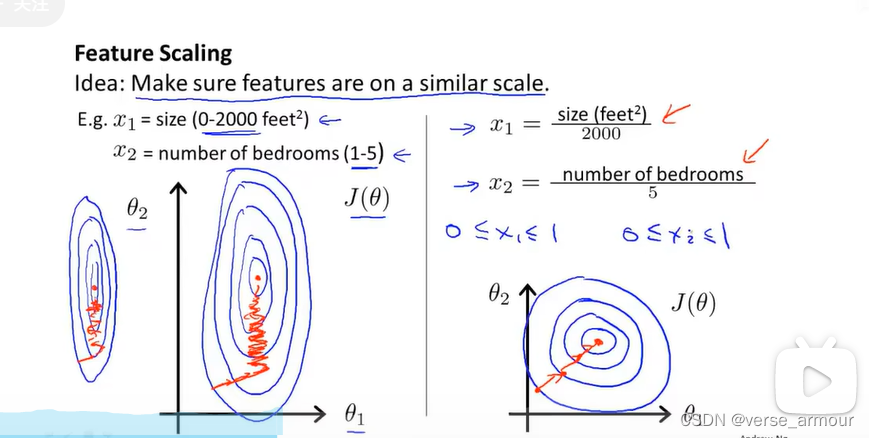
在这里插入图片描述

标准化（消除量纲影响）的作用：让代价等值线变得更圆，而梯度的方向是方向导数下降最快的方向，即与等高线垂直的方向，所以，让等值线变得更圆可以让梯度下降算法快速收敛，得到代价最小的参数值。

在这里插入图片描述

均值归一化处理（Mean normalization）
$\mu_1$ ：样本均值
$s_1$ ：样本区间
S1既可以是训练集合取值的范围：最大值和最小值之差，也可以使用标准方差，和正态分布的标准化有点类似。

（3）多元梯度下降法——学习率（learning rate : $\alpha$ ）

1. 判断梯度下降算法是否收敛—— $J(\theta)$ -No. of iterations函数

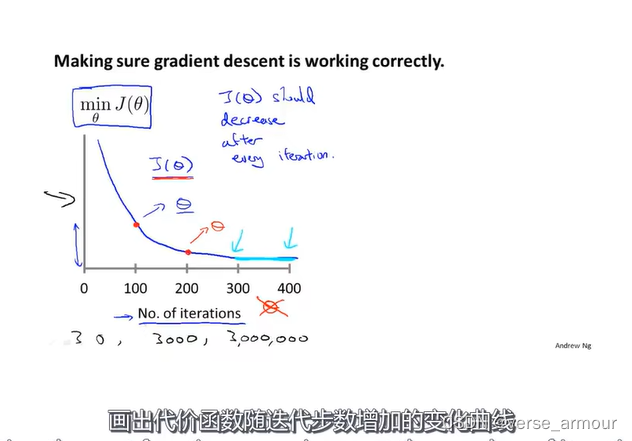
在这里插入图片描述

画出代价函数最小值随迭代步数增加的变化曲线，可以通过这种曲线判断梯度下降算法是否已经收敛

2. 判断梯度下降算法是否收敛——自动的收敛测试

如果代价函数 $J(\theta)$ 一步迭代后的下降小于一个很小的值 $\epsilon$ ,这个测试就判断函数已收敛。
在这里插入图片描述

通常要选择一个合适的阈值 $\epsilon$ 非常困难，因此为了检查梯度下降算法是否收敛通常采用第一种方法。

3. Making sure gradient descent is working correctly——setting appropriate learning rate

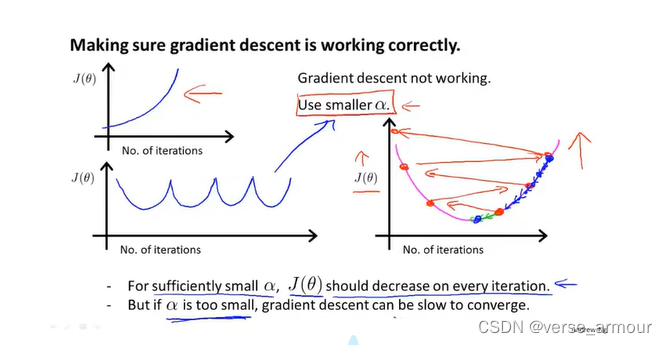
在这里插入图片描述
how to choose $\alpha$

运行梯度下降算法时，每隔10倍取一个 $\alpha$ ，对于不同的 $\alpha$ 的值绘制 $J(\theta)$ 随迭代步数变化的曲线，选择一个使 $J(\theta)$ 快速下降的一个 $\alpha$ 的值。

学习率通常情况下确实不需要更新。这里说的是找一个适合迭代的学习率的值；
当你选择一个特别小的学习率时，可以不用更新，但是这会造成大量时间浪费；
对于大数据样本，加速收敛就是刚开始选择大学习率，随着迭代减小学习率。

4-5.特征和多项式回归

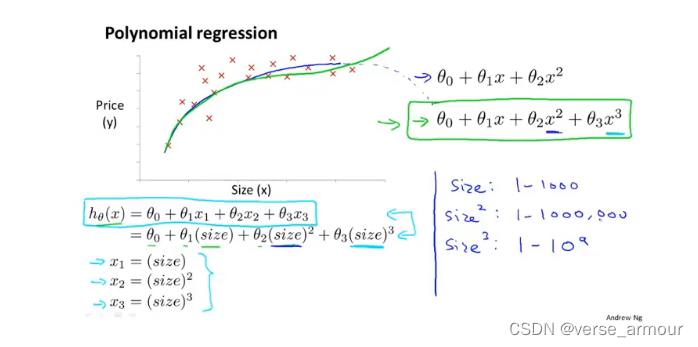
在这里插入图片描述

4-6.正规方程（区别于迭代方法的直接解法）

1.梯度下降和正规方程

梯度下降	正规方程
经过多次迭代收敛到全局最小值；特征缩放在梯度下降法中很有必要；需要选择学习率	提供了求 $\theta$ 的解析解法，不需要运行迭代算法，可以一次性求解 $\theta$ 的最优值；特征缩放在正规方程法中不必要；不需要选择学习率

对比：什么时候用梯度下降？什么时候用正规方程？

在这里插入图片描述
因为高维矩阵求逆会很time-consuming，因此当特征数量达到一定程度（10000以上）会考虑用梯度下降算法不用正规方程。

2.正规方程

####（1）数学原理
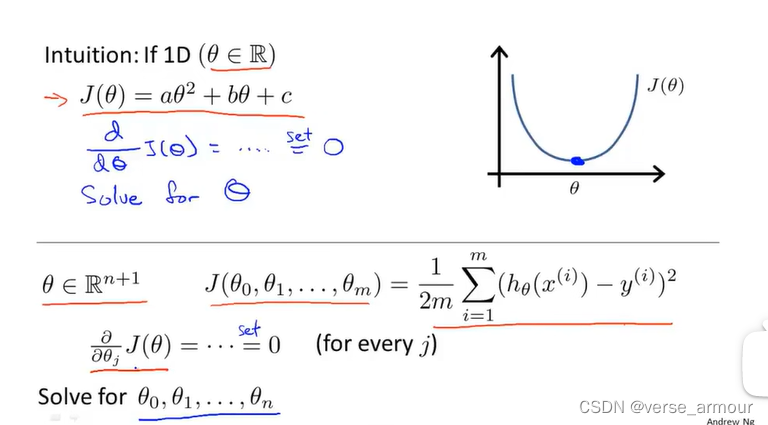在这里插入图片描述求出偏导数为0时 $\theta$ 的值，即是的代价函数 $J(\theta)$ 最小化的 $\theta$ 值。此处线性回归的代价函数是一个凸函数，只有一个全局最优解。对于凸优化来说，局部最优解就是全局最优解。

（2）example:训练样本数量m=4

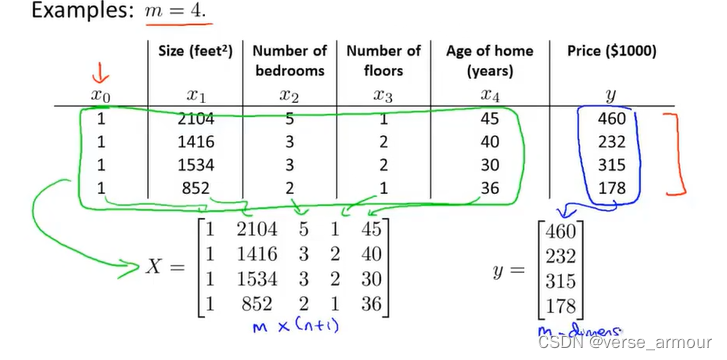
在这里插入图片描述
列方程：
$X\theta=y$
解方程：

因为 $X$ 不一定是一个可逆矩阵（一个可逆矩阵必定是一个方阵），因此要先对 $X$ 乘其转置，将其转化为一个可逆矩阵。

这里的 $X^TX$ 也未必可逆，还要满足其行列式等于0。这里对其求逆其实是求的伪逆矩阵，并且这里是左逆矩阵。
$\theta=(X^TX)^{-1}X^Ty$

3.关于梯度下降算法和正规方程算法的应用广度

随着我们用的学习算法越来越复杂，例如分类算法（classification algorithm）、逻辑回归算法/对数几率回归或对率回归（西瓜书译法）（logistic regression algorithm）,我们会发现珍贵方程算法不适用于那些更复杂的学习算法，因此我们还是不得不使用梯度下降算法。但是针对线性回归（linear regression）问题，正规方程是梯度下降更快的替代算法。