java基础操作4——java使用欧式距离计算三维空间两点之间的绝对距离

在实际项目中，计算两个坐标点的距离算是比较常见的问题。具体可参考如下文章：

https://blog.csdn.net/w10463672p/article/details/136877796

但是涉及到三维空间的距离计算，或者准确说是两点的相似度，需要用到欧式距离算法或者其他数学方法。

此算法计算的距离衡量的是多维空间中两个点间的绝对距离，属于矢量单位

一.欧式距离基本概念

欧几里得距离（Euclidean Distance）也称欧式距离，它以古希腊数学家欧几里得命名，是最常见的距离度量，用来衡量多维空间中两个点间的绝对距离，也就是两点之间最短的直线距离。在图上是用点的 N 个属性构成两个 N 维向量并计算欧几里得距离。

 详细说明参考：https://www.ultipa.cn/document/ultipa-graph-analytics-algorithms/euclidean-distance/v4.0

1.向量

向量是高等数学的基本概念，低维空间中的向量是比较容易理解和表达的。下图分别展示了二维空间、三维空间中向量 A、B 和坐标轴之间的关系以及它们之间的夹角 θ：

对图中两点进行比较时，用指定的 N 个数值类属性构成两个 N 维向量。

2.欧几里得距离

在二维空间中，欧几里得距离公式为：

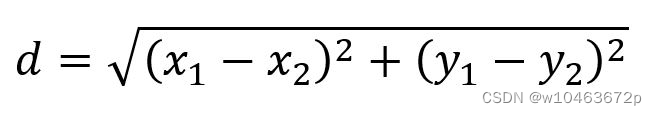
在三维空间中，欧几里得距离公式为：

推广到 n 维空间，欧几里得距离公式为：

其中，xi1 表示第一个点的第 i 维坐标，xi2 表示第二个点的第 i 维坐标。

欧几里得距离的取值范围是 [0,+∞]，数值越小越相似。

3.标准化欧几里得距离

标准化欧几里得距离是对欧几里得距离的一种改进方案，标准化欧几里得距离的取值范围是 [0,1]，数值越大越相似。

Ultipa 的标准化欧几里得距离计算公式为：

二.实现方案

根据欧式距离公式可以有如下的实现方法：

public static double coordinatesDistanceCount3D(PositionVo p1,
                                                PositionVo p2){
        double distance = 
                Math.sqrt((p1.getLongitude() - p2.getLongitude()) * (p1.getLongitude() - p2.getLongitude())
                + (p1.getLatitude() - p2.getLatitude()) * (p1.getLatitude() - p2.getLatitude())
                + (p1.getHeight() - p2.getHeight()) * (p1.getHeight() - p2.getHeight())
        );
        return distance;
    }

三.结果验证

1.计算跨度很大的两点距离

2.计算近距离的两点距离

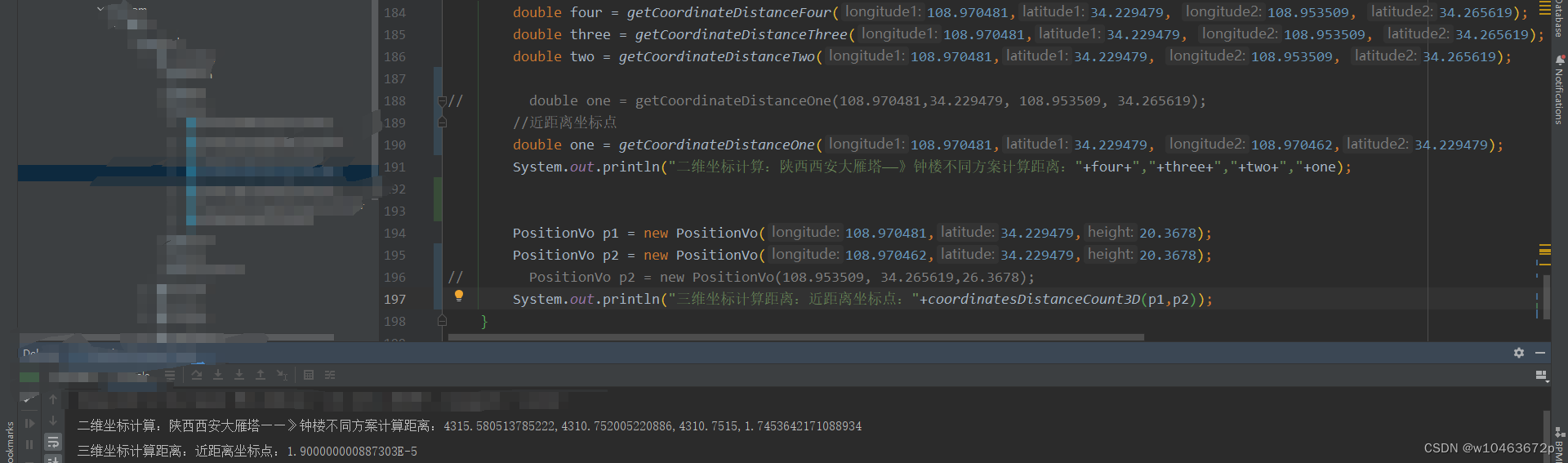
3.使用两个相同的点计算距离

注意：

通过以上数据测试说明，欧式距离公式判断的是数据相似度，并非实际的单位数据。