石墨烯能带结构（考虑三近邻），两种方法对比（1）构造哈密顿（2）matlab 后处理wannier90hr.dat （晶体规范）

原创

已于 2024-01-14 23:30:48 修改

· 2k 阅读

14 ·

版权

文章标签：

#matlab #数据库 #人工智能

于 2024-01-11 02:57:04 首次发布

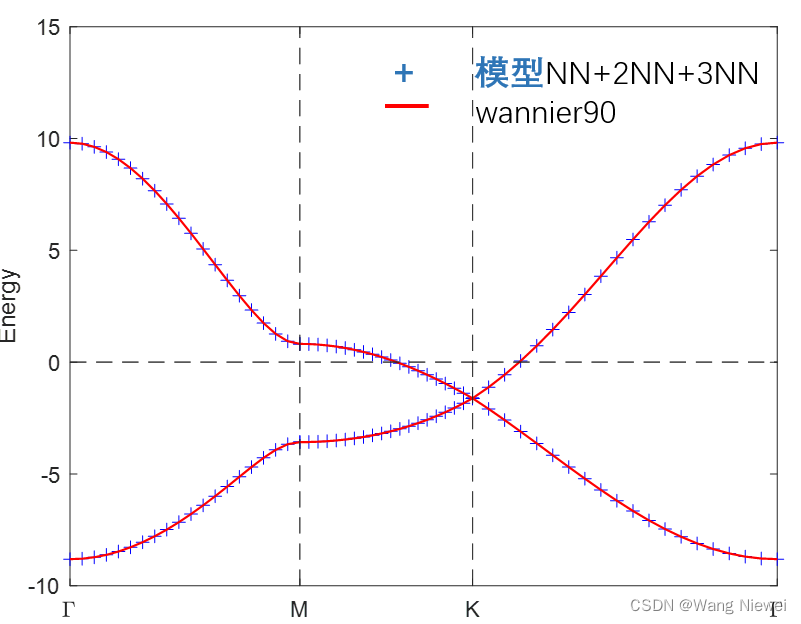
单层石墨烯能带图。方法一用+表示，方法2红色实线表示

(1)根据原胞构建哈密顿

%%Nie-Wei Wang,2024-1-8 (分解版，有基础)
clear all
%%%%%%%%晶格矢量 正格矢量
a1=[2.4682263781246880    0.0000000000000000    0.0000000000000000];           
a2=[-1.2341131890623440    2.1375467457960933    0.0000000000000000];            
a3=[0.0000000000000000    0.0000000000000000   10.0000000000000000];
% C1=[0.0000018561517373 -0.0000018561604471  0.5000000000000000];
% C2=[0.6666682727452335  0.3333317562640553  0.5000000000000000];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
V=dot(a1,cross(a2,a3));%  %%%晶胞体积

b1=2*pi*cross(a2,a3)/V; %%%%倒格矢量
b2=2*pi*cross(a3,a1)/V;
b3=2*pi*cross(a1,a2)/V;

a1=a1(1:2);                     %晶格矢量a1 二维
a2=a2(1:2);                     %晶格矢量a2
 
b1=b1(1:2);                     %%%倒空间晶格矢量b1，二维
b2=b2(1:2);                     %%%倒格矢b2
 
gamma=[0 0];                    %%%高对称点gamma 
M=1/2*b1;                       %%%高对称点M    
K=1/3*b1+1/3*b2;                %%%高对称点K   


kn=20;     %两个高对称点之间分成有kn个点
% Gamma-M段  每个高对称点都有两个 150和151都是M点
kx(1:kn)=linspace(gamma(1),M(1),kn);
ky(1:kn)=linspace(gamma(2),M(2),kn);
% M-K段
kx(kn+1:2*kn)=linspace(M(1),K(1),kn);
ky(kn+1:2*kn)=linspace(M(2),K(2),kn);
% K-Gamma段
kx(2*kn+1:3*kn)=linspace(K(1),0,kn);
ky(2*kn+1:3*kn)=linspace(K(2),0,kn);
k=zeros(3*kn,2);
k(:,1)=kx;