JADE
在本节中,我们提出一种新的差分进化算法JADE。该算法采用"DE/current-to-pbest"变异策略(带有可选存档机制),并通过自适应方式调整控制参数F和CR。JADE沿用了第II节公式(4)和(5)所描述的交叉与选择操作。


A. DE/Current-to-pbest
DE/rand/1是差分进化算法中最早提出的变异策略[1][2],也被认为是文献中最为成功且应用最广泛的方案[31]。然而,文献[6]指出DE/best/2可能具有优于DE/rand/1的特性,文献[32]则表明DE/best/1在多数技术问题的研究中表现更优。此外,文献[33]的作者认为融入最优解信息是有益的,并在其算法中采用了DE/current-to-best/1策略。相较于DE/rand/k类策略,诸如DE/current-to-best/k和DE/best/k这类贪婪策略通过融入最优解信息,在进化搜索中获得了更快的收敛速度。然而,这种最优解信息也可能导致种群多样性下降,进而引发早熟收敛等问题。
针对现有贪婪策略(式2和式3)收敛速度快但可靠性不足的问题,本文提出一种新型变异策略——“DE/current-to-pbest with optional archive”,作为本文提出的自适应DE算法JADE的核心基础。

如图1所示,在DE/current-to-pbest/1策略(无存档机制)中,变异向量按如下方式生成:

其中,
x
b
e
s
t
,
g
p
x_\mathrm{best,g}^p
xbest,gp 是从当前种群中前
100
p
%
100p\%
100p%(
p
∈
(
0
,
1
]
p\in(0,1]
p∈(0,1])的精英个体中随机选取的,
F
i
F_i
Fi是与个体
x
i
x_i
xi 相关联的变异因子,其值通过后文式(10)提出的自适应机制在每一代重新生成。DE/current-to-pbest本质上是DE/current-to-best策略的推广形式——通过随机选取前
100
p
%
100p\%
100p%精英个体中的任一解,取代DE/current-to-best中单一全局最优解的角色。
新近探索的劣势解相较于当前种群,能够为进化方向提供额外的有效信息。设A为存档的劣势解集合,P为当前种群。在带存档机制的DE/current-to-pbest/1策略中,变异向量生成方式如下:
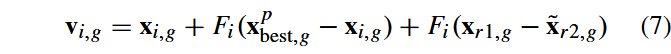
其中,
x
i
,
g
x_{i,g}
xi,g、
𝑥
𝑟
1
,
𝑔
𝑥_{𝑟1,𝑔}
xr1,g和
𝑥
p
b
e
s
t
,
𝑔
𝑥_{pbest,𝑔}
xpbest,g的选取方式与式(6)中相同(均从当前种群P中选择),而
x
~
r
2
,
g
\tilde{\mathbf{x}}_{r2,g}
x~r2,g 则是从当前种群P与存档A的并集𝑃∪𝐴中随机选取的。
存档操作的设计力求简洁,以避免产生显著的计算开销。存档初始化为空集,在每代进化过程中,根据式(5)的选择操作被淘汰的父代解会被添加至存档。若存档规模超过预设阈值(例如NP),则通过随机移除部分解以维持存档容量为NP。显然,当设置存档规模为零时,式(7)即退化为式(6)的特例。
该档案库不仅提供了关于进化方向的信息,还能够有效提升种群的多样性。此外,如后续参数自适应调整公式(10)-(12)所示,我们通过鼓励使用较大的F值来增强种群多样性。因此,尽管算法会偏向潜在最优解(可能为局部极小值)的进化方向,但所提出的DE/current-to-pbest/1算法仍能有效避免陷入局部极小。简而言之,DE/rand/1算法在无特定方向偏好的情况下,仅在相对较小的区域内进行搜索;而结合档案库机制的DE/current-to-pbest/1算法则在更大的搜索区域内开展探索,且其搜索方向会偏向于有潜力的进化方向。
JADE的伪代码如表I所示。接下来介绍F和C R的参数自适应。

B. Parameter Adaptation
在第g代时,每个个体xi的交叉概率CRi均独立地根据均值为
μ
C
R
μ_{CR}
μCR 、标准差为0.1的正态分布生成。

然后截断为[0,1]。将
S
C
R
S_{CR}
SCR表示为第g代所有成功交叉概率
C
R
i
CR_i
CRi的集合。均值
μ
C
R
μ_{CR}
μCR被初始化为0.5,并在每代结束时按如下方式更新:

其中c是0和1之间的正常数,
m
e
a
n
A
(
⋅
)
meanA(·)
meanA(⋅)是通常的算术平均值。
类似地,在第g代时,每个个体
x
i
x_i
xi的变异因子
F
i
F_i
Fi均独立地根据位置参数
μ
F
μ_F
μF、尺度参数0.1的柯西分布生成。

当
F
i
≥
1
F_i≥1
Fi≥1时将其截断为1,若
F
i
≤
0
F_i≤0
Fi≤0则重新生成。令
S
F
S_F
SF表示第g代中所有成功变异因子的集合。柯西分布的位置参数
μ
F
μ_F
μF被初始化为0.5,并在每代结束时按如下方式更新:

其中,meanL(·) 表示莱默平均(Lehmer mean)。

C. Explanations of the Parameter Adaptation
μ C R μ_{CR} μCR的自适应调整遵循以下核心原则:较优的控制参数值能够产生具有更高生存概率的个体,因此这些参数值应当被传递到后续进化代际中。其核心机制在于记录近期成功的交叉概率值,并利用这些历史信息指导新一代 C R i CR_i CRi的生成。公式(8)中设定较小标准差的原因在于:若标准差过大,参数调整效率将显著降低——例如在标准差趋近无穷大的极端情况下,截断正态分布将与 μ C R μ_{CR} μCR的实际取值完全无关。
与 C R CR CR的调整相比, μ F μ_F μF的适配包含两项独特操作:首先, F i F_i Fi的生成采用截断柯西分布。与正态分布相比,柯西分布能更有效地实现变异因子的多样化,从而避免在贪婪变异策略(如DE/best、DE/current-to-best和DE/current-to-pbest)中经常出现的早熟收敛现象——这种现象通常发生在变异因子高度集中于某个特定值时。
其次, μ F μ_F μF 的适配过程通过采用Lehmer均值(如公式12所示)而非 μ C R μ_{CR} μCR 调整中使用的算术均值,赋予较大成功变异因子更高权重。这种Lehmer均值有助于传播更大的变异因子,从而提升进化进度率。相反, S F S_F SF 的算术均值往往会小于变异因子的最优值,导致 μ F μ_F μF偏小并引发后期早熟收敛。 μ F μ_F μF 偏小的趋势主要源于进化搜索中成功概率与进度率之间的差异:采用较小 F i F_i Fi 的DE/current-to-pbest策略本质上类似于(1+1)进化策略(ES)[23],两者都在基向量的小邻域内生成后代。对于(1+1)ES而言,已有研究表明(在corridor and sphere 函数上严格证明[23][34]),变异方差越小通常成功概率越高。但趋近于0的变异方差显然会导致进化停滞。因此,通过赋予较大成功变异因子更高权重来实现更快进化进度,是一种简洁而高效的解决方案。
关于公式(9)和(11)中的常数c:当c=0时,系统不进行参数自适应调整;反之,成功的 C R i CR_i CRi 或 F i F_i Fi 的"生命周期"约为1/c代——具体而言,经过1/c代后,当c趋近于零时,原有的 μ C R μ_{CR} μCR 或 μ F μ_F μF值会按 ( 1 − c ) 1 / c (1−c)^{1/c} (1−c)1/c→1/e≈37%的比例衰减。
D. Discussion of Parameter Settings
经典差分进化算法(DE)包含两个需要用户调整的控制参数F和CR。这些参数具有问题依赖性,因此通常需要繁琐的试错过程才能为特定问题找到合适的取值。与之相反,JADE算法新引入的两个参数c和p预计对不同问题具有不敏感性——这源于它们在JADE中的特定作用:c控制参数自适应速率,p决定变异策略的贪婪程度。如第五节所示,JADE通常在1/c∈[5,20](即 μ C R μ_{CR} μCR 和 μ F μ_F μF值的生命周期为5-20代)且p∈[5%,20%]时表现最优,这意味着变异过程中我们仅考虑前5%-20%的高质量解。
Code
JADE.m
JADE算法。
%**************************************************************************************************
%Reference: J. Zhang and A. C. Sanderson, "JADE: adaptive differential evolution
% with optional external archive," IEEE Trans. Evolut. Comput., vol. 13,
% no. 5, pp. 945-958, 2009.
%
% Note: We obtained the MATLAB source code from the authors, and did some
% minor revisions in order to solve the 25 benchmark test functions,
% however, the main body was not changed.
%**************************************************************************************************
clc;
clear all;
tic;
format long;
format compact;
'JADE'
% Choose the problems to be tested. Please note that for test functions F7
% and F25, the global optima are out of the initialization range. For these
% two test functions, we do not need to judge whether the variable violates
% the boundaries during the evolution after the initialization.
problemSet = [1 : 6 8 : 24];
for problemIndex = 1 : 23
problem = problemSet(problemIndex)
% Define the dimension of the problem
n = 30;
popsize = 100;
switch problem
case 1
% lu: define the upper and lower bounds of the variables
lu = [-100 * ones(1, n); 100 * ones(1, n)];
% Load the data for this test function
load sphere_func_data
A = []; M = []; a = []; alpha = []; b = [];
case 2
lu = [-100 * ones(1, n); 100 * ones(1, n)];
load schwefel_102_data
A = []; M = []; a = []; alpha = []; b = [];
case 3
lu = [-100 * ones(1, n); 100 * ones(1, n)];
load high_cond_elliptic_rot_data
A = []; a = []; alpha = []; b = [];
if n == 2, load elliptic_M_D2,
elseif n == 10, load elliptic_M_D10,
elseif n == 30, load elliptic_M_D30,
elseif n == 50, load elliptic_M_D50,
end
case 4
lu = [-100 * ones(1, n); 100 * ones(1, n)];
load schwefel_102_data
A = []; M = []; a = []; alpha = []; b = [];
case 5
lu = [-100 * ones(1, n); 100 * ones(1, n)];
load schwefel_206_data
M = []; a = []; alpha = []; b = [];
case 6
lu = [-100 * ones(1, n); 100 * ones(1, n)];
load rosenbrock_func_data
A = []; M = []; a = []; alpha = []; b = [];
case 7
lu = [0 * ones(1, n); 600 * ones(1, n)];
load griewank_func_data
A = []; a = []; alpha = []; b = [];
if n == 2, load griewank_M_D2,
elseif n == 10, load griewank_M_D10,
elseif n == 30, load griewank_M_D30,
elseif n == 50, load griewank_M_D50,
end
case 8
lu = [-32 * ones(1, n); 32 * ones(1, n)];
load ackley_func_data
A = []; a = []; alpha = []; b = [];
if n == 2, load ackley_M_D2,
elseif n == 10, load ackley_M_D10,
elseif n == 30, load ackley_M_D30,
elseif n == 50, load ackley_M_D50,
end
case 9
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load rastrigin_func_data
A = []; M = []; a = []; alpha = []; b = [];
case 10
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load rastrigin_func_data
A = []; a = []; alpha = []; b = [];
if n == 2, load rastrigin_M_D2,
elseif n == 10, load rastrigin_M_D10,
elseif n == 30, load rastrigin_M_D30,
elseif n == 50, load rastrigin_M_D50,
end
case 11
lu = [-0.5 * ones(1, n); 0.5 * ones(1, n)];
load weierstrass_data
A = []; a = []; alpha = []; b = [];
if n == 2, load weierstrass_M_D2, ,
elseif n == 10, load weierstrass_M_D10,
elseif n == 30, load weierstrass_M_D30,
elseif n == 50, load weierstrass_M_D50,
end
case 12
lu = [-pi * ones(1, n); pi * ones(1, n)];
load schwefel_213_data
A = []; M = []; o = [];
case 13
lu = [-3 * ones(1, n); 1 * ones(1, n)];
load EF8F2_func_data
A = []; M = []; a = []; alpha = []; b = [];
case 14
lu = [-100 * ones(1, n); 100 * ones(1, n)];
load E_ScafferF6_func_data
if n == 2, load E_ScafferF6_M_D2, ,
elseif n == 10, load E_ScafferF6_M_D10,
elseif n == 30, load E_ScafferF6_M_D30,
elseif n == 50, load E_ScafferF6_M_D50,
end
A = []; a = []; alpha = []; b = [];
case 15
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load hybrid_func1_data
A = []; M = []; a = []; alpha = []; b = [];
case 16
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load hybrid_func1_data
if n == 2, load hybrid_func1_M_D2,
elseif n == 10, load hybrid_func1_M_D10,
elseif n == 30, load hybrid_func1_M_D30,
elseif n == 50, load hybrid_func1_M_D50,
end
A = []; a = []; alpha = []; b = [];
case 17
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load hybrid_func1_data
if n == 2, load hybrid_func1_M_D2,
elseif n == 10, load hybrid_func1_M_D10,
elseif n == 30, load hybrid_func1_M_D30,
elseif n == 50, load hybrid_func1_M_D50,
end
A = []; a = []; alpha = []; b = [];
case 18
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load hybrid_func2_data
if n == 2, load hybrid_func2_M_D2,
elseif n == 10, load hybrid_func2_M_D10,
elseif n == 30, load hybrid_func2_M_D30,
elseif n == 50, load hybrid_func2_M_D50,
end
A = []; a = []; alpha = []; b = [];
case 19
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load hybrid_func2_data
if n == 2, load hybrid_func2_M_D2,
elseif n == 10, load hybrid_func2_M_D10,
elseif n == 30, load hybrid_func2_M_D30,
elseif n == 50, load hybrid_func2_M_D50,
end
A = []; a = []; alpha = []; b = [];
case 20
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load hybrid_func2_data
if n == 2, load hybrid_func2_M_D2,
elseif n == 10, load hybrid_func2_M_D10,
elseif n == 30, load hybrid_func2_M_D30,
elseif n == 50, load hybrid_func2_M_D50,
end
A = []; a = []; alpha = []; b = [];
case 21
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load hybrid_func3_data
if n == 2, load hybrid_func3_M_D2,
elseif n == 10, load hybrid_func3_M_D10,
elseif n == 30, load hybrid_func3_M_D30,
elseif n == 50, load hybrid_func3_M_D50,
end
A = []; a = []; alpha = []; b = [];
case 22
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load hybrid_func3_data
if n == 2, load hybrid_func3_HM_D2,
elseif n == 10, load hybrid_func3_HM_D10,
elseif n == 30, load hybrid_func3_HM_D30,
elseif n == 50, load hybrid_func3_HM_D50,
end
A = []; a = []; alpha = []; b = [];
case 23
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load hybrid_func3_data
if n == 2, load hybrid_func3_M_D2,
elseif n == 10, load hybrid_func3_M_D10,
elseif n == 30, load hybrid_func3_M_D30,
elseif n == 50, load hybrid_func3_M_D50,
end
A = []; a = []; alpha = []; b = [];
case 24
lu = [-5 * ones(1, n); 5 * ones(1, n)];
load hybrid_func4_data
if n == 2, load hybrid_func4_M_D2,
elseif n == 10, load hybrid_func4_M_D10,
elseif n == 30, load hybrid_func4_M_D30,
elseif n == 50, load hybrid_func4_M_D50,
end
A = []; a = []; alpha = []; b = [];
case 25
lu = [2 * ones(1, n); 5 * ones(1, n)];
load hybrid_func4_data
if n == 2, load hybrid_func4_M_D2,
elseif n == 10, load hybrid_func4_M_D10,
elseif n == 30, load hybrid_func4_M_D30,
elseif n == 50, load hybrid_func4_M_D50,
end
A = []; a = []; alpha = []; b = [];
end
% Record the best results
outcome = [];
%Main body which was developed by the authors
time = 1; % 当前运行次数
% The total number of runs
totalTime = 1;
while time <= totalTime
rand('seed', sum(100 * clock)); % 设置随机种子
% Initialize the main population
popold = repmat(lu(1, :), popsize, 1) + rand(popsize, n) .* (repmat(lu(2, :) - lu(1, :), popsize, 1));
valParents = benchmark_func(popold, problem, o, A, M, a, alpha, b); % 计算适应度值 NP*1
c = 1/10;
p = 0.05;
CRm = 0.5; % 初始化CR均值
Fm = 0.5; % 初始化F均值
Afactor = 1; % 用于控制外部存档和种群大小的比例
archive.NP = Afactor * popsize; % the maximum size of the archive 外部存档的大小
archive.pop = zeros(0, n); % the solutions stored in te archive 劣解
archive.funvalues = zeros(0, 1); % the function value of the archived solutions 劣解的适应度值
%% the values and indices of the best solutions 升序排序,并得到对应的索引,最好的值在最前面
[valBest, indBest] = sort(valParents, 'ascend');
FES = 0; % 函数评估次数
while FES < n * 10000 %& min(fit)>error_value(problem)
pop = popold; % the old population becomes the current population
if FES > 1 && ~isempty(goodCR) && sum(goodF) > 0 % If goodF and goodCR are empty, pause the update
CRm = (1 - c) * CRm + c * mean(goodCR);
Fm = (1 - c) * Fm + c * sum(goodF .^ 2) / sum(goodF); % Lehmer mean
end
% Generate CR according to a normal distribution with mean CRm, and std 0.1
% Generate F according to a cauchy distribution with location parameter Fm, and scale parameter 0.1
[F, CR] = randFCR(popsize, CRm, 0.1, Fm, 0.1); % 每个个体对应一个F和CR
r0 = [1 : popsize];
popAll = [pop; archive.pop]; % PUA
[r1, r2] = gnR1R2(popsize, size(popAll, 1), r0); % 生成参数r1和r2
% Find the p-best solutions
pNP = max(round(p * popsize), 2); % choose at least two best solutions
randindex = ceil(rand(1, popsize) * pNP); % select from [1, 2, 3, ..., pNP]
randindex = max(1, randindex); % to avoid the problem that rand = 0 and thus ceil(rand) = 0
pbest = pop(indBest(randindex), :); % randomly choose one of the top 100p% solutions
% == == == == == == == == == == == == == == == Mutation == == == == == == == == == == == == ==
vi = pop + F(:, ones(1, n)) .* (pbest - pop + pop(r1, :) - popAll(r2, :));
vi = boundConstraint(vi, pop, lu); % 越界处理
% == == == == = Crossover == == == == =
mask = rand(popsize, n) > CR(:, ones(1, n)); % mask is used to indicate which elements of ui comes from the parent
% choose one position where the element of ui doesn't come from the parent
rows = (1 : popsize)';cols = floor(rand(popsize, 1) * n)+1;
jrand = sub2ind([popsize n], rows, cols); % 使用 sub2ind 将子脚标转换为线性索引
mask(jrand) = false; % 确保每个个体至少有一个维度来自突变向量
ui = vi; ui(mask) = pop(mask);
valOffspring = benchmark_func(ui, problem, o, A, M, a, alpha, b); % 计算适应度值
FES = FES + popsize; % 函数评估次数+popsize
% == == == == == == == == == == == == == == == Selection == == == == == == == == == == == == ==
% I == 1: the parent is better; I == 2: the offspring is better
[valParents, I] = min([valParents, valOffspring], [], 2);
popold = pop;
archive = updateArchive(archive, popold(I == 2, :), valParents(I == 2)); % 更新外部存档
popold(I == 2, :) = ui(I == 2, :);
goodCR = CR(I == 2);
goodF = F(I == 2);
[valBest indBest] = sort(valParents, 'ascend');
end
outcome = [outcome min(valParents)]; % 记录本次运行的最优值
time = time + 1;
end
sort(outcome)
mean(outcome)
std(outcome)
end
toc;
randFCR.m
为种群中的每个个体生成F和CR。
function [F,CR] = randFCR(NP, CRm, CRsigma, Fm, Fsigma)
% this function generate CR according to a normal distribution with mean "CRm" and sigma "CRsigma"
% If CR > 1, set CR = 1. If CR < 0, set CR = 0.
% this function generate F according to a cauchy distribution with location parameter "Fm" and scale parameter "Fsigma"
% If F > 1, set F = 1. If F <= 0, regenrate F.
%
% Version: 1.1 Date: 11/20/2007
% Written by Jingqiao Zhang (jingqiao@gmail.com)
%% generate CR
CR = CRm + CRsigma * randn(NP, 1);
CR = min(1, max(0, CR)); % truncated to [0 1]
%% generate F
F = randCauchy(NP, 1, Fm, Fsigma);
F = min(1, F); % truncation
% we don't want F = 0. So, if F<=0, we regenerate F (instead of trucating it to 0)
pos = find(F <= 0);
while ~ isempty(pos)
F(pos) = randCauchy(length(pos), 1, Fm, Fsigma);
F = min(1, F); % truncation
pos = find(F <= 0);
end
% Cauchy distribution: cauchypdf = @(x, mu, delta) 1/pi*delta./((x-mu).^2+delta^2)
function result = randCauchy(m, n, mu, delta)
% http://en.wikipedia.org/wiki/Cauchy_distribution
result = mu + delta * tan(pi * (rand(m, n) - 0.5));
updateArchive.m
更新存档并输入解决方案
步骤1:将新解决方案添加至存档
步骤2:移除重复项
步骤3:如有需要,随机删除部分解决方案以维持存档容量
function archive = updateArchive(archive, pop, funvalue)
% Update the archive with input solutions
% Step 1: Add new solution to the archive
% Step 2: Remove duplicate elements
% Step 3: If necessary, randomly remove some solutions to maintain the archive size
%
% Version: 1.1 Date: 2008/04/02
% Written by Jingqiao Zhang (jingqiao@gmail.com)
if archive.NP == 0, return; end
if size(pop, 1) ~= size(funvalue,1), error('check it'); end
% Method 2: Remove duplicate elements
popAll = [archive.pop; pop ];
funvalues = [archive.funvalues; funvalue ];
[dummy IX]= unique(popAll, 'rows');
if length(IX) < size(popAll, 1) % There exist some duplicate solutions
popAll = popAll(IX, :);
funvalues = funvalues(IX, :);
end
if size(popAll, 1) <= archive.NP % add all new individuals
archive.pop = popAll;
archive.funvalues = funvalues;
else % randomly remove some solutions
rndpos = randperm(size(popAll, 1)); % equivelent to "randperm";
rndpos = rndpos(1 : archive.NP);
archive.pop = popAll (rndpos, :);
archive.funvalues = funvalues(rndpos, :);
end
gnR1R2.m
选择两个随机个体r1和r2。
function [r1, r2] = gnR1R2(NP1, NP2, r0)
% gnA1A2 generate two column vectors r1 and r2 of size NP1 & NP2, respectively
% r1's elements are choosen from {1, 2, ..., NP1} & r1(i) ~= r0(i)
% r2's elements are choosen from {1, 2, ..., NP2} & r2(i) ~= r1(i) & r2(i) ~= r0(i)
%
% Call:
% [r1 r2 ...] = gnA1A2(NP1) % r0 is set to be (1:NP1)'
% [r1 r2 ...] = gnA1A2(NP1, r0) % r0 should be of length NP1
%
% Version: 2.1 Date: 2008/07/01
% Written by Jingqiao Zhang (jingqiao@gmail.com)
NP0 = length(r0);
r1 = floor(rand(1, NP0) * NP1) + 1;
for i = 1 : inf
pos = (r1 == r0);
if sum(pos) == 0
break;
else % regenerate r1 if it is equal to r0
r1(pos) = floor(rand(1, sum(pos)) * NP1) + 1;
end
if i > 1000, % this has never happened so far
error('Can not genrate r1 in 1000 iterations');
end
end
r2 = floor(rand(1, NP0) * NP2) + 1;
for i = 1 : inf
pos = ((r2 == r1) | (r2 == r0));
if sum(pos)==0
break;
else % regenerate r2 if it is equal to r0 or r1
r2(pos) = floor(rand(1, sum(pos)) * NP2) + 1;
end
if i > 1000, % this has never happened so far
error('Can not genrate r2 in 1000 iterations');
end
end
boundConstraint.m
越界处理。
function vi = boundConstraint (vi, pop, lu)
% if the boundary constraint is violated, set the value to be the middle
% of the previous value and the bound
%
% Version: 1.1 Date: 11/20/2007
% Written by Jingqiao Zhang, jingqiao@gmail.com
[NP, D] = size(pop); % the population size and the problem's dimension
%% check the lower bound
xl = repmat(lu(1, :), NP, 1);
pos = vi < xl; % NP*D找到所有违反约束下界的值的位置
vi(pos) = (pop(pos) + xl(pos)) / 2;
%% check the upper bound
xu = repmat(lu(2, :), NP, 1);
pos = vi > xu; % NP*D找到所有违反约束上界的值的位置
vi(pos) = (pop(pos) + xu(pos)) / 2;
参考
[1] Jingqiao Zhang, Sanderson A C. JADE: Adaptive differential evolution with optional external archive[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958.

























 2495
2495

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










