一、实现例子
李航《统计学方法》p29 例2.1
正例:x1=(3,3), x2=(4,3),
负例:x3=(1,1)
二、最终效果
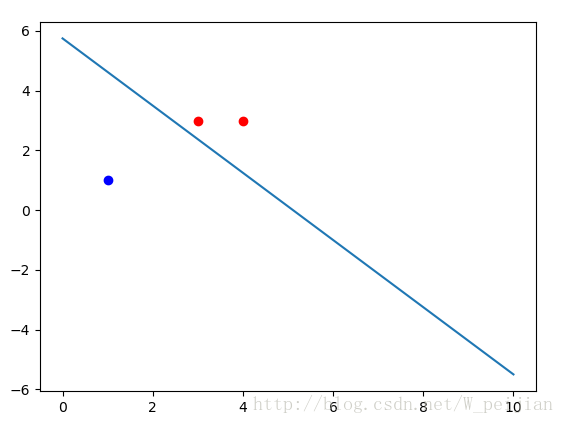
三、代码实现
import numpy as np
import matplotlib.pyplot as plt
p_x = np.array([[3, 3], [4, 3], [1, 1]])
y = np.array([1, 1, -1])
plt.figure()
for i in range(len(p_x)):
if y[i] == 1:
plt.plot(p_x[i][0], p_x[i][1], 'ro')
else:
plt.plot(p_x[i][0], p_x[i][1], 'bo')
w = np.array([1, 0])
b = 0
delta = 1
for i in range(100):
choice = -1
for j in range(len(p_x)):
if y[j] != np.sign(np.dot(w, p_x[0]) + b):
choice = j
break
if choice == -1:
break
w = w + delta * y[choice]*p_x[choice]
b = b + delta * y[choice]
line_x = [0, 10]
line_y = [0, 0]
for i in range(len(line_x)):
line_y[i] = (-w[0] * line_x[i]- b)/w[1]
plt.plot(line_x, line_y)
plt.savefig("picture.png")




















 277
277

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








