- 品质因数 Q = U L U s Q=\frac{ U_L}{U_s} Q=UsUL,即电感上的电压比上输入电压,是分析和比较谐振电路的一个重要辅助参数。
- 不同参数的RLC电路在频率响应上的差异,是通过Q值反映出来的。在谐振电路中,它们有以下不同点
1.它们都在谐振点出现峰值,在其领域都有较大的幅值输出,表明RLC串联电路具有在全频域内选择各自频振信号的性能;
2.当信号频率偏移谐振点,输出信号从峰值下降,表明信号对非谐振频率有抑制作用(简称抑非能力)。抑非能力与Q值成正比,能力越强,通频带越窄,电路选择性越好;能力越弱,通频带越宽,电路选择性变差。
二阶传递函数的品质因数
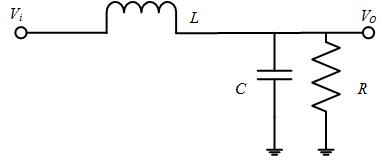
- 传递函数 G = V o V i = 1 S 2 L C + S L / R + 1 G={\frac{V_o}{V_i}}={\frac{1}{S^2LC+SL/R+1}} G=ViVo=S2LC+SL/R+11
- 品质因数
Q
=
R
C
L
Q=R\sqrt{\frac{C}{L}}
Q=RLC
LC滤波器伯德图如下图所示:

- 品质因数Q确定了响应曲线在交接频率处的峰值大小,如图Q=20,那么谐振下输出电压是输入电压的20倍。一般认为Q值越大,则滤波器欠阻尼状态,当Q=0.707,得到临界阻尼,谐振频率的增益比其直流值低3dB。-3dB是0.707的对数,意味着下降约30%。
- 电阻对交接频率影响较小,但其对Q的影响是显著地。L和C的串联寄生电阻越大,Q值越小。
- 工程师一般用阻尼系数 ξ = 1 2 Q ξ={\frac{1}{2Q}} ξ=2Q1,高Q值对应小ξ。























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








