PCA和SVD区别和联系

前言：

PCA(principal component analysis)和SVD(Singular value decomposition)是两种常用的降维方法，在机器学习等领域有广泛的应用。本文主要介绍这两种方法之间的区别和联系。

一、PCA:

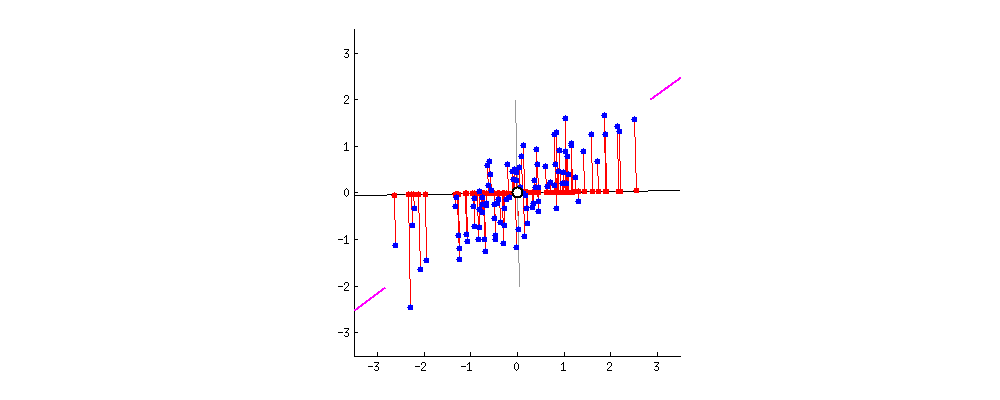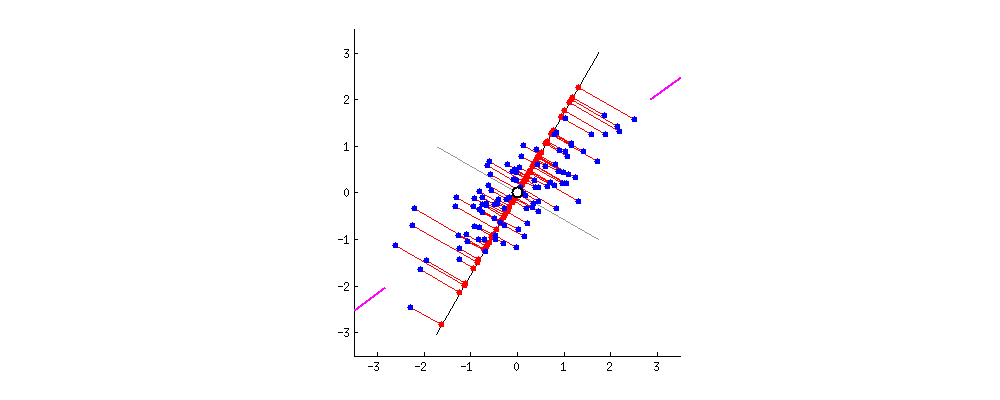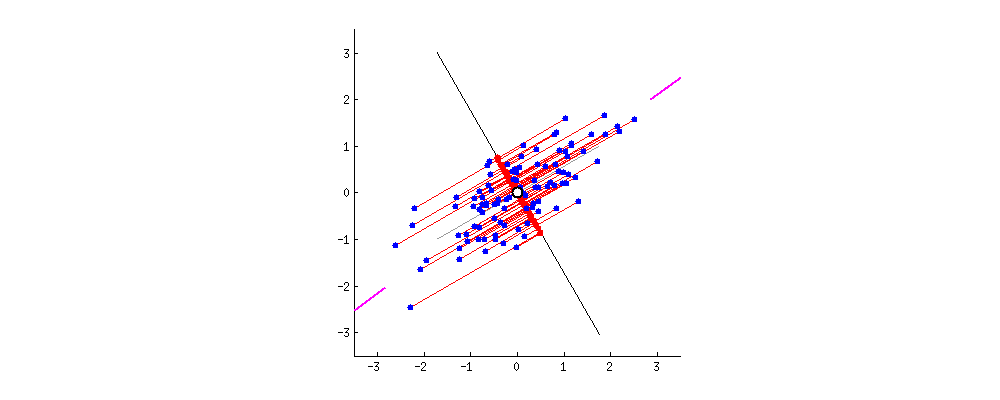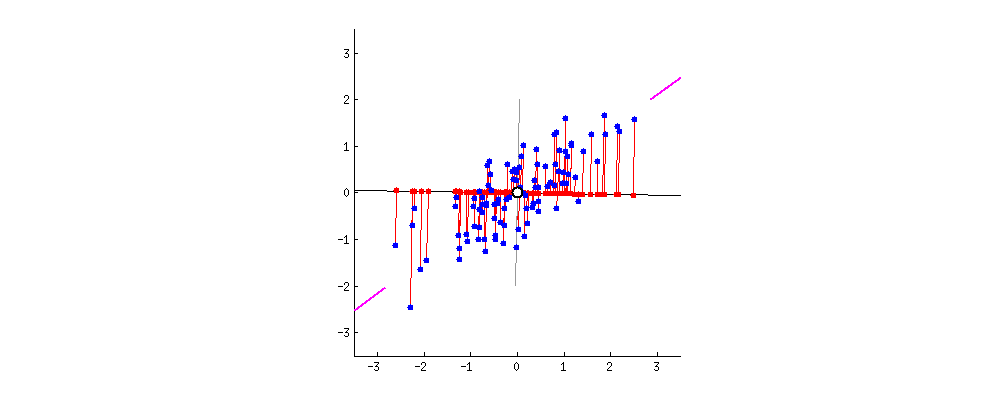
图1.寻找主成分方向

    PCA的中文名叫做主成分分析，是降维和去噪的一种重要方法。PCA选取包含信息量最多的方向对数据进行投影。其投影方向可以从最大化方差或者最小化投影误差两个角度理解（详细推导见机器学习圣经PRML）。假设有$n\times d$矩阵X，每一行是一个$d$维样本$x_i$，寻找投影方向$v_j$以最大化投影方差：

$$\begin{equation} \max_{v_j} \frac{1}{n} \sum_{i=1}^n (x_i v_j - \bar{x})^\top (x_i v_j - \bar{x}) = v_j^\top C v_j,\;\;\; s.t.\; v_j^\top \cdot v_j = 1 \end{equation}$$

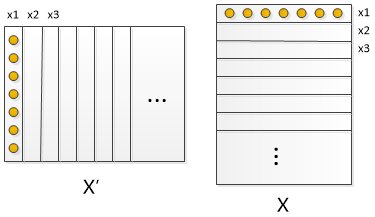
图2.X’X

    其中$\bar{x}$是均值，为了简化公式，本文假设$X$已经进行过零均值化处理，即$\bar{x}=0$；$v_j$是数据的投影方向。$d\times d$ 协方差矩阵$C = \frac{1}{n} \sum_{i=1}^n (x_i)^\top (x_i ) = \frac{1}{n} X^\top X$。由于$C$是实对称矩阵，可以进行对角化处理：

$$\begin{equation} C = VLV^\top \end{equation}$$
$d\times d$正交矩阵$V$的每一列是特征向量，$d\times d$矩阵$L$对角线上的每一个元素是特征值，且特征值按递减顺序排列。把$C$ 代回式子$v_j^\top C v_j$：

$$\begin{equation} v_j^\top C v_j = v_j^\top VLV^\top v_j = \lambda_j \end{equation}$$
     $\lambda_j$是特征向量 $v_j$对应的特征值。可以发现当投影方向是 $C$的最大特征值对应的特征向量时，投影方向上数据的方差最大。所以用PCA进行降维时通常选取较大特征值对应的特征向量作为投影方向：$XV_k$， $V_k$是最大的k个特征值对应的特征向量矩阵。

二、SVD:

    如果对$X$做奇异值矩阵分解（SVD分解）：

$$\begin{equation} X = USV^\top \end{equation}$$
对角阵$S$对角线上的元素是奇异值，$U$和$V$是正交矩阵：$U^\top U=I, V^\top V=I$。把$X$的奇异值分解代入协方差矩阵：
$$\begin{equation} C = \frac{1}{n} X^\top X = \frac{1}{n} VS^\top U^\top USV^\top = V\frac{S^2}{n} V^\top \end{equation}$$
$d\times d$正交矩阵$V$的每一列是特征向量，不难发现特征值与奇异值之间存在着对应关系$\lambda_i = S_{ii}^2/n$。对$X$主成分方向进行投影：
$$\begin{equation} XV_k = USV^\top V_k = U_k S_k \end{equation}$$
$U_k$包含$U$的前k列，$S_k$包含$S$左上角的$k\times k$个元素。

三、区别与联系：

SVD另一个方向上的主成分

    SVD可以获取另一个方向上的主成分，而PCA只能获得单个方向上的主成分：

$$\begin{equation} \frac{1}{n} X X^\top = \frac{1}{n} USV^\top VS^\top U^\top = U\frac{S^2}{n} U^\top \end{equation}$$

SVD计算伪逆

    求解矩阵的最小二乘问题需要求伪逆，使用SVD可以很容易得到矩阵$X$的伪逆：

$$\begin{equation} X^+ = VS^{-1}U^\top \end{equation}$$

LSI

    隐语义索引（Latent semantic indexing，简称LSI）通常建立在SVD的基础上，通过低秩逼近达到降维的目的。

$$\begin{equation} X_k = \min_{A\; rank(A)=k} \parallel X - A\parallel \end{equation}$$
注意到PCA也能达到降秩的目的，但是PCA需要进行零均值化，且丢失了矩阵的稀疏性。

数值稳定性

    通过SVD可以得到PCA相同的结果，但是SVD通常比直接使用PCA更稳定。因为PCA需要计算$X^\top X$的值，对于某些矩阵，求协方差时很可能会丢失一些精度。例如Lauchli矩阵：

$$\begin{equation} X= \begin{bmatrix} 1 & 1 & 1\\ e & 0 & 0\\ 0 & e & 0\\ 0 & 0 & e\\ \end{bmatrix} \end{equation}$$
在Lauchli矩阵里， $e$是很小的数，$e^2$无法用计算机精确表示，从而计算 $X^\top X$会丢失 e <script type="math/tex" id="MathJax-Element-53">e</script>这部分信息。

四、参考资料

[1] Pattern Recognition and Machine Learning

[2] Mathematics Stack Exchange:http://math.stackexchange.com/questions/3869/what-is-the-intuitive-relationship-between-svd-and-pca

[3] Cross Validated:http://stats.stackexchange.com/questions/134282/relationship-between-svd-and-pca-how-to-use-svd-to-perform-pca