卡特兰数
从格点
(
0
,
0
)
(0,0)
(0,0)走到格点
(
n
,
n
)
(n,n)
(n,n),只能向右或向上走,不能穿过对角线,的路径的条数,称为卡特兰数
H
n
H_n
Hn。
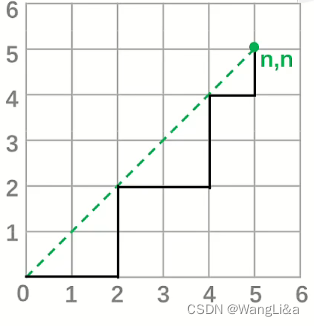
则有
H
0
=
1
H_0=1
H0=1。
通项公式:
- H n = ( 2 n n ) − ( 2 n n − 1 ) H_n=\begin{pmatrix} 2n\\ n \end{pmatrix}-\begin{pmatrix} 2n\\ n-1 \end{pmatrix} Hn=(2nn)−(2nn−1)
- H n = ( 2 n n ) n + 1 H_n=\frac {\begin{pmatrix} 2n\\ n \end{pmatrix}}{n+1} Hn=n+1(2nn)
- H n = 4 n − 2 n + 1 H n − 1 H_n=\frac{4n-2}{n+1}H_{n-1} Hn=n+14n−2Hn−1
折线法
证明一下卡特兰数的公式。
先证明公式1:
如果没有限制,那么路径总数是,从
2
n
2n
2n步移动之中,选出
n
n
n步向上走,另外
n
n
n步向右走的方案数
(
2
n
n
)
\begin{pmatrix} 2n\\ n \end{pmatrix}
(2nn)。
如果有限制,我们画出
y
=
x
+
1
y=x+1
y=x+1的函数图像,碰到这条线,意味着不合法。
把所有不合法的路径沿着这条图像对折过来,其终点必然是
(
n
−
1
,
n
+
1
)
(n-1,n+1)
(n−1,n+1)。
换句话说,所有到达
(
n
−
1
,
n
+
1
)
(n-1,n+1)
(n−1,n+1)的路径,都对应着到达
(
n
,
n
)
(n,n)
(n,n)的一条不合法路径。因此答案就是
(
2
n
n
)
−
(
n
+
1
+
n
−
1
n
−
1
)
\begin{pmatrix} 2n\\ n \end{pmatrix}-\begin{pmatrix} n+1+n-1\\ n-1 \end{pmatrix}
(2nn)−(n+1+n−1n−1)
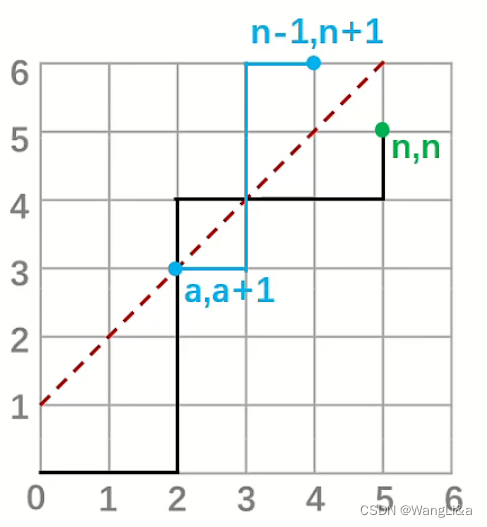
QED.
证明一下公式2:
(
2
n
n
)
−
(
2
n
n
−
1
)
\begin{pmatrix} 2n\\ n \end{pmatrix}-\begin{pmatrix} 2n\\ n-1 \end{pmatrix}
(2nn)−(2nn−1)
=
(
2
n
)
!
n
!
n
!
−
(
2
n
)
!
(
n
+
1
)
!
(
n
−
1
)
!
=\frac{(2n)!}{n!n!}-\frac {(2n)!}{(n+1)!(n-1)!}
=n!n!(2n)!−(n+1)!(n−1)!(2n)!
=
(
2
n
)
!
n
!
(
n
−
1
)
!
n
−
(
2
n
)
!
n
!
(
n
−
1
)
!
(
n
+
1
)
=\frac{(2n)!}{n!(n-1)!n}-\frac {(2n)!}{n!(n-1)!(n+1)}
=n!(n−1)!n(2n)!−n!(n−1)!(n+1)(2n)!
=
(
2
n
)
!
n
!
(
n
−
1
)
!
⋅
(
1
n
−
1
n
+
1
)
=\frac{(2n)!}{n!(n-1)!}\cdot\left(\frac{1}{n}-\frac 1{n+1}\right)
=n!(n−1)!(2n)!⋅(n1−n+11)
=
(
2
n
)
!
n
!
(
n
−
1
)
!
n
−
(
2
n
)
!
n
!
(
n
−
1
)
!
(
n
+
1
)
=\frac{(2n)!}{n!(n-1)!n}-\frac {(2n)!}{n!(n-1)!(n+1)}
=n!(n−1)!n(2n)!−n!(n−1)!(n+1)(2n)!
=
(
2
n
)
!
n
!
(
n
−
1
)
!
⋅
(
1
n
−
1
n
+
1
)
=\frac{(2n)!}{n!(n-1)!}\cdot\left(\frac{1}{n}-\frac 1{n+1}\right)
=n!(n−1)!(2n)!⋅(n1−n+11)
=
(
2
n
)
!
n
!
(
n
−
1
)
!
⋅
1
n
(
n
+
1
)
=\frac{(2n)!}{n!(n-1)!}\cdot\frac {1}{n(n+1)}
=n!(n−1)!(2n)!⋅n(n+1)1
=
(
2
n
)
!
n
!
n
!
⋅
1
n
+
1
=\frac{(2n)!}{n!n!}\cdot\frac {1}{n+1}
=n!n!(2n)!⋅n+11
=
(
2
n
n
)
⋅
1
n
+
1
=\begin{pmatrix} 2n\\ n \end{pmatrix}\cdot\frac {1}{n+1}
=(2nn)⋅n+11
QED.
证明一下公式3:
留作习题,读者自证不难。
常见情况
特点:一种操作不能超过另一种操作,或操作之间不能有交集。
例如:
- 一个由 n n n个 0 0 0, n n n个 1 1 1组成的长度为 2 n 2n 2n的字符串,满足所有前缀中, 1 1 1的个数不能超过 0 0 0的个数,这样的子串数量。
- 包含
n
n
n组括号的合法表达式的数量。
(想要括号序列合法,必须保证所有前缀中,左括号的数量大于等于右括号的数量) - 一个栈的进栈序列为
1
,
2
,
.
.
.
,
n
1,2,...,n
1,2,...,n,则出栈序列的可能数量。
(必须保证出栈数量小于等于进栈数量) - 在圆上选择
2
n
2n
2n个点,连接起来形成
n
n
n条不相交的弦的方案数。
(把 n n n条不相交的弦映射为括号序列,把弦的左端映射为左括号,右端映射为右括号) - 通过连接顶点将
n
+
2
n+2
n+2条边的正多边形分为
n
n
n个三角形的方案数(三角剖分)。
(想要保证分为 n n n个三角形,必须保证连接的线不相交) -
n
n
n个节点可以构造多少颗不同的二叉树?
(考虑对 n + 2 n+2 n+2条边的多边形三角剖分,把剖分得出的三角形抽象为一个节点,对它相邻的三角形连边,最后得出必定是一颗二叉树。) - 一段连乘积有多少种运算次序?
(相当于给连乘积加括号)
公式法
事实上有:
H
n
=
∑
i
=
0
n
−
1
H
i
H
n
−
i
−
1
H_n=\overset{n-1}{\underset{i=0}\sum}H_iH_{n-i-1}
Hn=i=0∑n−1HiHn−i−1
可以从两个方面来证明一下:
- 出栈序列
考虑 i i i是最后一个出栈的数,则 [ 1 , i − 1 ] [1,i-1] [1,i−1]在 i i i进栈之前就出栈了,情况数有 H i − 1 H_{i-1} Hi−1种,而 i i i后面的 n − i n-i n−i个数,则必然在 i i i出栈前就出栈了,情况数有 H n − i H_{n-i} Hn−i种,枚举这个 i i i,得到
H n = ∑ i = 1 n H i − 1 H n − i = ∑ i = 0 n − 1 H i H n − i − 1 H_n=\overset{n}{\underset{i=1}\sum}H_{i-1}H_{n-i}=\overset{n-1}{\underset{i=0}\sum}H_iH_{n-i-1} Hn=i=1∑nHi−1Hn−i=i=0∑n−1HiHn−i−1 - 格点计数
我们知道,在格点卡特兰数的要求中,路径不能越过对角线。我们可知,在走到终点之前的一步,一定是向上走的:

红色表示最后一步。
显然,碰到对角线之后,一定是向右走的,我们枚举对角线上的一个点,使得走完向右走的那一步之后,不能越过新的对角线,统计的路径条数:

绿色,枚举的位置。
红色,最后一步。
蓝色,新的对角线。
此时我们发现,从底下走到绿色圆圈,不能越过对角线。与从绿色箭头走到红色圆圈,不能越过蓝线,是两个更小的卡特兰数问题,因此可以用乘法原理计数。
我们注意到,我们枚举的一种新的情况,在我们枚举的更旧的情况中都属于不合法情况,不会被重复统计。
QED.
用公式同样可以解释各种卡特兰数的情况。
- 一个由
n
n
n个
0
0
0,
n
n
n个
1
1
1组成的长度为
2
n
2n
2n的字符串,满足所有前缀中,
1
1
1的个数不能超过
0
0
0的个数,这样的子串数量。
注意到最后一个字符一定是 1 1 1,枚举一个位置的 0 0 0,使得这个 0 0 0与末尾的那个 1 1 1匹配,转化为格点计数的情况。 - 包含
n
n
n组括号的合法表达式的数量。
同理。 - 一个栈的进栈序列为
1
,
2
,
.
.
.
,
n
1,2,...,n
1,2,...,n,则出栈序列的可能数量。
同理。 - 在圆上选择
2
n
2n
2n个点,连接起来形成
n
n
n条不相交的弦的方案数。
同理,枚举一个点与最后那个点(任意指定一个固定的点为最后的点)连接成弦。 - 通过连接顶点将
n
+
2
n+2
n+2条边的正多边形分为
n
n
n个三角形的方案数(三角剖分)。
同理4。 -
n
n
n个节点可以构造多少颗不同的二叉树?
枚举根节点有 i i i个左子树,则就会有 n − i − 1 n-i-1 n−i−1个右子树,显然。
斯特林数
第一类斯特林数
定义 [ n m ] \begin{bmatrix}n\\ m\end{bmatrix} [nm]表示 n n n元集合划分为 m m m个非空环排列的方案数,即无符号第一类斯特林数,或简称为第一类斯特林数,斯特林轮换数。
第一类斯特林数有递推式:
[
n
m
]
=
[
n
−
1
m
−
1
]
+
(
n
−
1
)
[
n
−
1
m
]
\begin{bmatrix} n\\ m \end{bmatrix}=\begin{bmatrix} n-1\\ m-1 \end{bmatrix}+(n-1)\begin{bmatrix} n-1\\ m \end{bmatrix}
[nm]=[n−1m−1]+(n−1)[n−1m]
递推式容易证明,留作习题。
第二类斯特林数
定义 { n m } \begin{Bmatrix} n\\ m \end{Bmatrix} {nm}表示将 n n n元集合划分为 m m m个非空子集的方案数,即第二类斯特林数,或斯特林子集数。
第二类斯特林数有递推式:
{
n
m
}
=
{
n
−
1
m
−
1
}
+
m
{
n
−
1
m
}
\begin{Bmatrix} n\\ m \end{Bmatrix}=\begin{Bmatrix} n-1\\ m-1 \end{Bmatrix}+m\begin{Bmatrix} n-1\\ m \end{Bmatrix}
{nm}={n−1m−1}+m{n−1m}
递推式容易证明,留作习题。
其他
- 两类斯特林数的边界条件都是 s [ 0 ] [ 0 ] = 1 s[0][0]=1 s[0][0]=1。
- 从递推式可以看出,斯特林数增长比组合数还要快。
- 斯特林数用于解决计数问题,以及用于斯特林反演。这些较复杂,单独讨论。
后记
于是皆大欢喜。




















 1660
1660











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








