MATLAB系列：矩阵运算笔记（一）

0x00 前言

文章中的文字可能存在语法错误以及标点错误，请谅解；

如果在文章中发现代码错误或其它问题请告知，感谢

0x01 矩阵

1.矩阵定义

矩阵是由m*n个数 a_ij (i = 1,2…,m,j = 1,2,…,n) 排列成m行n列，记成：
$$\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right)$$

该矩阵称为m* n 矩阵，记成A_{m *n} 。若m=n，则该矩阵称为n阶矩阵（n阶方阵）。

2.矩阵的生成

矩阵的生成有直接输入法、M文件生成法以及文本文件生成法。
1）直接输入法
可以再命令行窗口直接定义矩阵，若定义时“[ ]”内无内容，表示为一个空矩阵：

例1：
直接输入法定义矩阵1。

>> A = [1 2 3; 4 5 6; 7 8 9]

例2：
直接输入法定义矩阵2。

>> A = [1 1+i 2;2 4+2i 4]

2 ) M文件生成法
若矩阵的规模比较大，适合使用M脚本文件进行创建矩阵。

例3：
M文件生成发定义矩阵。

在M脚本文件中编写一个文件名为sample.m的M文件：
M文件中：

%%sample.m
A = [123 33 44 55 66 77 77 89 99 22;
      33 44 33 987 53 3 32 45 12 32;
      203 303 0 03 32 23 00 5 34 34;
      2 333 444 94 94 82 23 43 43 3;]

编写后保存为sample.m格式文件。

命令行窗口中：

>>sample

3）文本文件生成法
建立文本文件，在命令行窗口调用该文件

例4：
文本文件生成法定义矩阵。

在记事本中创建名为“test.txt”文本：

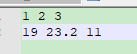
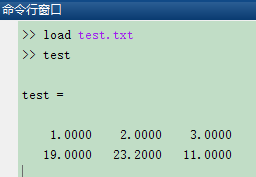
在命令行窗口中调用以及使用：

>> load test.txt
>> test

3.创建特殊矩阵

可以使用函数直接创建特殊矩阵：

>>eye(n) %%创建n*n单位矩阵
>>eye(m, n) %%创建m*n单位矩阵
>>ones(n) %%创建n*n全1矩阵
>>ones(m,n) %%创建m*n全1矩阵
>>zeros(m,n) %%创建全0矩阵
>>rand(n) %%在[0,1]区间内创建一个n*n均匀分布的随机矩阵
>>rand(m, n) %%在[0,1]区间内创建一个m*n均匀分布的随机矩阵
>>compan(P) %%创建系数向量是P的多项式的伴随矩阵
>>diag(v) %%创建一个向量v中的元素为对角的对角矩阵
>>hilb(n) %%创建n*n的Hilbert矩阵
>>magic(n) %%生成n阶魔方矩阵
>>sparse(A) %%将矩阵A转化为稀疏矩阵形式，即由A的非零元素和下标构成稀疏矩阵S。若A本身为稀疏矩阵，则返回A本身。

4.矩阵的修改

矩阵可以进行元素修改、抽取等操作。
1）矩阵元素修改

命令名	说明
D = [A;b c]	A为原矩阵，B、C中包含要扩充的元素，D为扩充之后的矩阵
A(m,:)	删除A的第m行
A(:,n)	删除A的第n列
A(m,n) = a	对A的第m行n列元素进行赋值
A(m,:) = [a b …]	对A的第m行进行赋值
A(:,n) = [a b …]	对A的第n列进行赋值

例5：
修改矩阵。

>> A = [2 3 4; 5 6 7];
>> B = eye(2);
>> C = zeros(2,1);
>> D = [A;B C]

2）矩阵变维
矩阵变维使用reshape()函数，调用格式为：reshape(X,m,n)，将矩阵变维为m行n列矩阵。

例6：
矩阵变维。

>> A = 1:12;
>> B = reshape(A,2,6)

3）矩阵的变向

命令名	说明
rot(90)	将A矩阵逆时针方向旋转90度
rot(90,k)	将A逆时针方向旋转90*k度，k可为整数
fliplr(A)	将A左右翻转
flipud(A)	将A上下翻转
flipdim(X,dim)	dim = 1时对行翻转，dim = 2时队列翻转

例7：
矩阵变向。

>> A = 1:12;
>> C = zeros(3,4);
>> C(:) = A(:)
>>flipdim(C,1)
>>flipdim(C,2)

4）矩阵抽取
对矩阵进行对角元素或上下三角矩阵元素抽取。

命令名	说明
diag(A,k)	抽取矩阵A的第k条对角线上的元素向量。k = 0抽取主对角线，k>0抽取上方第k条对角线上的元素，k<0时抽取下方第k条对角线上的数
diag(A)	抽取主对角线
diag(v,k)	使得v为所得矩阵第k条对角线上的元素向量
diag(v)	使得v为所得矩阵主对角线上的元素向量
tril(A)	提取矩阵A的主下三角形
tril(A,k)	提取矩阵A的第k条对角线下面部分（包括第k条对角线）
triu(A)	提取矩阵A的主上三角形
triu(A,k)	提取矩阵A的第k条对角线上面部分（包括第k条对角线）

例8：
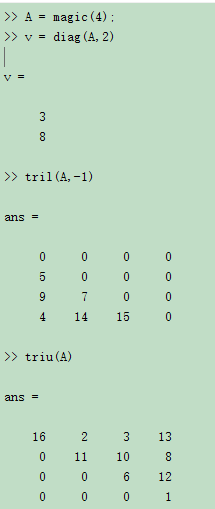
矩阵抽取。

>> A = magic(4);
>> v = diag(A,2)
>> tril(A,-1)
>> triu(A)

0x02 矩阵数学运算

矩阵基本运算包括加、减、乘、数乘、点乘、乘方、左除、右除、求逆。
加、减、乘对应运算符为+、-、* 。
矩阵除法为MATLAB独有的，分为左除和右除，相应运算符为\和/。方程AX=B的解是X=A\B，方程XA的解是X=A\B。

1.矩阵加法

设A=（a_ij），B=（b_ij），都是m*n矩阵，矩阵A与矩阵B的和记为A+B，规定为：
$$A+B=\left[\begin{array}{cccc}{a}_{11}+b_{11}& a_{12}+b_{12}& ...& a_{1n}+b_{1n}\\ a_{21}+b_{21}& a_{22}+b_{22}& ...& a_{2n}+b_{2n}\\ ...& ...& ...& ...\\ a_{m1}+b_{m1}& a_{m2}+b_{m2}& ...& a_{mn}+b_{mn}\end{array}\right]$$
满足交换律和结合率：
交换律：A+B=B+A
结合率：（A+B）+C = A+（B+C）

例8：
矩阵验证矩阵交换律和结合律。

>> A = [1 2 3 4;5 6 7 8];
>> B = [2 4 6 8;1 3 5 7];
>> C = [8 7 6 5;4 3 2 1];
>> A+B
>> B+A
>>(A+B)+C
>>A+(B+C)

2.矩阵乘法

1）数乘运算
数$\lambda$与矩阵A=（aij）乘积记为$\lambda$A或A$\lambda$：

$$\lambda A=\left[\begin{array}{cccc}\lambda a_{11}& \lambda a_{12}& ...& \lambda a_{1n}\\ \lambda a_{21}& \lambda a_{22}& ...& \lambda a_{2n}\\ ...& ...& ...& ...\\ \lambda a_{m1}& \lambda a_{m2}& ...& \lambda a_{mn}\end{array}\right]$$

矩阵满足下列规律：
$\lambda$（$\mu$A） = ($\lambda$$\mu$)A
($\lambda$+$\mu$)A = $\lambda$A +$\mu$A
$\lambda$(A+B) = $\lambda$A+$\lambda$B

例9：
数乘运算。

>> A = [1 2 3; 4 5 6];
>> 5*A

2）乘运算
设A（a_ij）是一个 m * s矩阵 ，B=b(_ij)是一个s* n矩阵，规定A与B的积为一个m*n矩阵C=（c_ij）：
c_ij = a_i1+b_1j+a_i2+b_2j+…+a_isb_sj
i = 1,2,…,m; j = 1,2,…,n。

A列数要和B行数相同；
C行数等于A行数，C列数等于B列数；
C的m行n列元素值等于A的m行元素与B的列元素对应的值积的和。

$$\left[\begin{array}{cccc}{a}_{i1}& a_{i2}& ...& a_{in}\end{array}\right]\left[\begin{array}{c}{b}_{1j}\\ b_{2j}\\ ...\\ b_{sj}\end{array}\right]=C_{ij}$$
例10：
矩阵乘法。

>> A = [1 2 3; 4 5 6];
>> B = [2 3 4; 5 6 4;2 3 4];
>> A*B

注意：AB $\cancel{=}$ BA
$$\left[\begin{array}{ccc}{a}_1& a_2& a_3\end{array}\right]\left[\begin{array}{c}{b}_1\\ b_2\\ b_2\end{array}\right]=\left[\begin{array}{c}{a}_1{b}_1+a_1{b}_2+a_1{b}_3\end{array}\right]$$

$$\left[\begin{array}{c}{a}_1\\ a_2\\ a_2\end{array}\right]\left[\begin{array}{ccc}{b}_1& b_2& b_3\end{array}\right]=\left[\begin{array}{ccc}{a}_1{b}_1& a_1{b}_2& a_1{b}_3\\ a_2{b}_1& a_2{b}_2& a_2{b}_3\\ a_3{b}_1& a_3{b}_2& a_3{b}_3\end{array}\right]$$
3)点乘运算
矩阵点乘运算指将两个矩阵中同位置元素进行相乘运算，将积保存在原位置组成新元素。

例11：
点乘运算。

>> A = [1 2 3; 4 5 6];
>> B = [2 3 4; 5 6 4];
>> A.*B

3.矩阵除法

左除A\B时，A的行数要和B的行数一致，计算右除A/B时，A的列数要和B的列数一致。
1）左除运算
矩阵的特殊性，AB$\cancel{=}$ BA，除法也需要区分左右。
线性方程组D*X=B，若D为非奇异矩阵，即它的逆矩阵inv（D）存在，则其解为X=inv(D)*B=D\B。符号“\”称为左除 ，即分母放在左边。左除条件为：B的行数等于D的阶数（D的行数和列数相同，简称阶数）。

例12：

>> A = [1 2;2 1];
>> B = [2 3;3 4];
>> C = A*B
>> D = A\C
>> E = inv(A)*C

2)右除运算
若方程组表示X*D=B，D为非奇异矩阵，即它的它的逆矩阵inv（D）存在，则其解为X=B*inv(D)=B/D。符号“/”称为右除，即分母放在右边。右除条件为：B的列数等于D的阶数（D的行数和列数相同，简称阶数）。

例13：

>> A = [1 2;2 1];
>> B = [2 3;3 4];
>> C = A*B
>> D = C/B
>> E = C*inv(B)

以上。

参考文档：
1.https://www.zybuluo.com/codeep/note/163962（Markdown 公式指导手册）
2.https://blog.csdn.net/u013647759/article/details/85635162(矩阵空格公式方程组)
3.https://blog.csdn.net/katherine_hsr/article/details/79179622（数学符号和公式）
4.天工在线.中文版MATLAB2018从入门到精通（实战案例版）[M].北京:中国水利水电出版社,2018.
5.https://blog.csdn.net/clam_clam/article/details/7184991