【论文阅读14】- GAN - 生成对抗网络增强 滑坡位移预测 性能

这篇文章主要探讨了如何利用生成对抗网络（GAN）来增强滑坡位移预测模型的性能，特别是在数据稀缺的情况下。文章提出了一种新型的GAN模型——RGAN-LS（ (Recurrent Generative Adversarial Networks for synthesizing LandSlide)），利用递归神经网络（RNN）来捕捉多变量时间序列数据中的复杂时间相关性，并通过生成合成样本来增强训练数据。

参考文献
Ge Q, Li J, Lacasse S, et al. Data-augmented landslide displacement prediction using generative adversarial network[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2024, 16(10): 4017-4033.

期刊
《岩石力学与岩土工程学报》
（Journal of Rock Mechanics and Geotechnical Engineering，JRMGE）

作者介绍
第一作者 葛琦(Qi Ge)
南京林业大学 土木工程学院 个人简介 谷歌学术 researchgate
通讯作者 刘忠强(Zhongqiang Liu)
挪威土工所 谷歌学术

原文代码 GitHub

摘要

---

滑坡是一种破坏性极强的自然灾害，在全球范围内造成严重的破坏和人员伤亡。准确预测滑坡位移对于有效的预警和风险管理至关重要。然而，现场测量数据的有限性一直是构建数据驱动模型（如先进的机器学习模型）的一大障碍。为应对这一挑战，本研究提出了一种基于生成对抗网络（GAN）（Generative Adversarial Networks）的数据增强框架，这是一种近年来在生成式人工智能领域的最新进展，旨在提高滑坡位移预测的准确性。该框架通过有效的数据增强手段扩展了有限的数据集。

本研究提出了一种循环生成对抗网络模型（RGAN-LS），专为生成逼真的多变量时间序列而设计，这些合成数据能够模拟真实滑坡现场监测数据的特征。RGAN-LS在训练过程中，除了传统的对抗损失外，还引入了定制的矩匹配损失，以捕捉时间序列数据中的时间动态特性和变量间的相关性。

随后，利用RGAN-LS生成的合成数据，对长短期记忆网络（LSTM）和粒子群优化-支持向量机（PSO-SVM）模型的滑坡位移预测性能进行了提升。在三峡库区的两个滑坡案例中，LSTM模型在使用增强数据训练后预测性能显著提高。例如，在Baishuihe滑坡案例中，平均均方根误差（RMSE）提升了16.11%，平均绝对误差（MAE）提升了17.59%。更重要的是，模型在滑坡突变阶段的响应能力也得到了增强，有助于实现更及时的预警。

然而，结果表明，静态的PSO-SVM模型在使用增强数据后仅获得了有限的改进，远不如LSTM等递归模型。进一步分析发现，在实例中，合成数据与真实数据的最佳比例为50%，可最大化模型性能的提升。这也表明，动态模型在增强训练数据后具有更强的鲁棒性和有效性。

通过使用强大的生成式人工智能方法，RGAN-LS能够生成高保真度的滑坡合成数据，这对于在训练数据有限的情况下提升先进机器学习模型的预测性能具有重要意义。此外，该方法还有潜力扩展到地质灾害风险管理以及其他相关研究领域的应用中。

---

关键词（Keywords）：

• 机器学习（Machine learning, ML）
• 时间序列（Time series）
• 生成对抗网络（Generative adversarial network, GAN）
• 三峡库区（Three Gorges reservoir, TGR）
• 滑坡位移预测（Landslide displacement prediction）

---

1. 引言

引出滑坡致灾话题–>滑坡预测

滑坡每年在世界各地的山区造成灾难性破坏和人员伤亡（Capobianco 等, 2022；Tehrani 等, 2022）。中国长江上游的三峡库区（TGR）地处滑坡地质灾害的高发区，已有成千上万处滑坡被记录（Tang 等, 2019；Juang, 2021）。滑坡位移是滑坡演化和稳定性最直观的表现形式之一，准确的位移预测有助于实现有效的预警和风险管理，在减少滑坡灾害损失方面起着关键作用。

滑坡预测方法分类

滑坡位移预测可以通过物理模型或现象学模型实现（Liu 等, 2020）。物理模型考虑滑坡几何形态（Kennedy 等, 2021）、土体变异性（Phoon 等, 2022）和地下水流动（Sun 等, 2021）等因素，有助于深入理解滑坡的本质过程（Gupta 等, 2023）。然而，由于材料数据稀缺性和复杂的边界条件，物理模型的预测精度可能受到限制（Jiang 等, 2023）。相比之下，现象学模型则侧重于位移与诱发因素之间的经验关系，提供了一种实用的预测方法（Zhang 等, 2022a）。

机器学习方法

近年来，人工智能（AI）的快速发展推动了基于机器学习（ML）的现象学模型在滑坡预测中的广泛应用，尤其是在三峡库区（Wang 等, 2022）。多种机器学习方法及非线性智能系统已在三峡库区多个水库滑坡案例中展现出优异的预测性能（Liao 等, 2020；Li 等, 2021a；Wang 等, 2023a）。目前，用于预测滑坡位移的机器学习模型大致可分为静态模型与动态模型。

常用方法

最常用的静态模型包括支持向量机（SVM）（Zhou 等, 2018）和极限学习机（ELM）（Cao 等, 2016；Huang 等, 2017），常与参数优化算法（如粒子群优化算法 PSO）结合形成混合模型，如 PSO-SVM（Zhang 等, 2021；Ma 等, 2022）和 PSO-ELM（Du 等, 2020；Zhu 等, 2022）。而动态模型则能够捕捉滑坡的时序动态特征，如长短期记忆网络（LSTM）（Xu 和 Niu, 2018；Xing 等, 2020）和门控循环单元（GRU）神经网络（Zhang 等, 2022b；Nava 等, 2023）。此外，为了支持风险知情决策并量化预测的不确定性，研究者提出了基于静态与动态方法的新型区间预测模型（Ma 等, 2018；Lian 等, 2020；Li 等, 2021b；Ge 等, 2022），该类模型预测的是位移的范围而非单点值。

存在问题

尽管 AI 的发展显著提高了滑坡位移的预测性能，但机器学习模型训练所需的数据稀缺问题仍未得到根本解决。当前先进的 ML 模型和复杂的网络结构需要大量训练数据以发挥其预测能力。然而，在实际中，现场监测数据常因设备、时间与人力资源成本高昂而稀缺。尽管三峡库区部分滑坡已有超过十年的连续监测数据，能够公开获取的位移数据仍然非常有限，仅约 100 组，每月更新一次（Gong 等, 2022；Ge 等, 2023）。数据的稀缺严重制约了复杂深度神经网络的有效训练。虽然预测算法已从静态模型演进至动态模型，但受限于训练数据不足，其预测精度仍难以大幅提升。

面对问题 引出GAN

为应对数据不足带来的挑战，一些研究尝试在有限数据条件下提升预测性能。例如，过采样方法可改善分类任务中的不平衡问题（Li 等, 2021b）；基于类似案例的迁移学习亦可提升位移预测的准确性（Long 等, 2022）。近年来，生成式人工智能（Generative AI）迅速发展，并在多个领域表现出显著潜力，为数据增强提供了有力手段，有望缓解数据稀缺问题。生成模型（如生成对抗网络 GANs（Goodfellow 等, 2014）、扩散模型 DMs（Ho 等, 2020）和大语言模型 LLMs（Min 等, 2021））可合成高度逼真的新型数据。GAN 通过生成器和判别器的对抗博弈学习真实数据分布，从而生成逼真的新数据，适合进行数据增强。通过学习滑坡位移数据的复杂分布，GAN 能生成新的时间序列样本，以扩展训练数据集，提高预测模型的准确性。

本文方法

因此，生成对抗网络的发展有望通过增强有限的现场测量数据，显著提升滑坡位移预测的性能。为解决机器学习滑坡预测中面临的数据匮乏问题，本研究提出一种新的解决方案：利用 GAN 生成模型合成滑坡数据，称为用于滑坡数据生成的循环生成对抗网络（RGAN-LS）。该模型以循环神经网络（RNN）为网络主干，能够捕捉时间序列数据中的时间依赖性。通过引入定制的损失函数（如矩匹配损失），RGAN-LS 可更准确地重建滑坡时间序列的统计特征和动态行为。

结果

本文利用 RGAN-LS 生成的时间序列数据对三峡库区两个滑坡实例进行数据增强训练，分别用于训练动态模型（LSTM）与静态模型（PSO-SVM）。结果表明，在使用增强数据训练后，LSTM 模型的预测性能显著提升，而 SVM 的提升则较为有限。此外，本研究进一步探讨了合成数据与真实数据的比例对模型性能的影响，验证了所提出 GAN 方法在缓解数据稀缺方面的有效性与鲁棒性。通过解决数据不足这一关键问题，本研究展示了结合生成式 AI 与机器学习技术在滑坡位移预测中的巨大潜力。RGAN-LS 模型的代码已在 GitHub 开源（RGAN-LS）。

---

2. 方法

2.1. 用于数据增强的生成对抗网络（GAN）

2.1.1. GAN 的基本结构

生成对抗网络（GAN）由 Goodfellow 等人于 2014 年首次提出，在合成真实感数据方面已在多种应用场景中展现出巨大潜力（Bendaoud 等, 2021；Li 等, 2023）。作为一种深度生成方法，GAN 包含两个主要组成部分（见图 1a）：生成器（记作 $G$）和判别器（记作 $D$）。这对深度神经网络以对抗的方式进行训练，并进行极小极大博弈。

生成器 $G$ 接收从高斯分布或均匀分布中采样得到的随机变量 $z$，并尝试输出能够准确表示真实样本分布的合成数据 $G(z)$。判别器 $D$ 是一个二分类器，其目标是区分真实数据 $x$ 和生成器输出的合成数据 $G(z)$。网络通过反向传播和判别器的输出进行优化。GAN 的训练目标是达到纳什均衡（Goodfellow et al., 2014），即生成器能够准确捕捉真实数据分布并生成足以“欺骗”判别器的逼真样本。

---

2.1.2. RGAN-LS 用于滑坡现场监测数据增强

本研究提出了一种用于滑坡多变量时间序列数据增强的生成对抗网络，称为 RGAN-LS (Recurrent Generative Adversarial Networks for synthesizing LandSlide)。该模型充分利用了循环神经网络（RNN）结构的优势，在生成器与判别器中均使用循环单元作为基本构建模块，以有效捕捉时间序列中的时序相关性。已有文献表明（Zhang 等, 2022b），RNN 单元（如 LSTM 与 GRU）可精准建模时间序列中的时序依赖与趋势。

本节以下内容将以 LSTM 单元为例，对 RGAN-LS 网络进行数学描述。实际实现中，亦可使用 GRU 单元代替 LSTM。

如图 1b 所示，RGAN-LS 中生成器的输入为一组潜在向量序列 { z t } t = 1 T \{z_t\}_{t=1}^T {zt​}t=1T​，每个 $z_t\in {\mathbb{R}}^k$，$k$ 表示潜在空间的维度。$z_t$ 从均匀分布中独立采样，代表潜在的“种子”因素，在通过生成器网络学习时，可生成与滑坡位移相关的模式。

生成器中的 LSTM 单元输出的是模拟的滑坡现场多变量时间序列数据，包括库水位、降雨量与周期性位移等。LSTM 单元通过门控机制调节信息流动，并有效缓解梯度消失问题。在每个时间步 $t$，LSTM 单元接收当前输入 $z_t$、前一时刻的状态 $C_{t-1}$ 与隐藏状态 $h_{t-1}$，并计算如下变量：

$$\begin{array}{rl}{i}_t& =\sigma (W_i{h}_{t-1}+U_i{z}_t+b_i)\\ f_t& =\sigma (W_f{h}_{t-1}+U_f{z}_t+b_f)\\ o_t& =\sigma (W_o{h}_{t-1}+U_o{z}_t+b_o)\\ {\tilde{C}}_t& =\tanh (W_c{h}_{t-1}+U_c{z}_t+b)\\ C_t& =f_t\odot C_{t-1}+i_t\odot {\tilde{C}}_t\\ h_t& =o_t\odot \tanh (C_t)\end{array}$$

其中，$\sigma$ 表示 Sigmoid 函数，$\odot$ 表示元素级乘法，$W$ 与 $U$ 分别为作用于隐藏状态与输入的权重矩阵，$b$ 为偏置项，$h_t$ 为当前时间步的隐藏状态，表示在监测周期内由历史信息所传递的当前状态。

随后，LSTM 输出的隐藏状态序列 { h t } t = 1 T \{h_t\}_{t=1}^T {ht​}t=1T​ 被输入到一个共享权重的全连接层中，通过 Sigmoid 激活函数变换后得到最终的合成多变量时间序列 { x t } t = 1 T \{x_t\}_{t=1}^T {xt​}t=1T​。

判别器 $D$ 的结构与生成器类似，也由一个循环单元和全连接层组成。不同的是，判别器的输入为真实时间序列 { x t } t = 1 T \{x_t\}_{t=1}^T {xt​}t=1T​ 或生成的时间序列 { x ^ t } t = 1 T \{\hat{x}_t\}_{t=1}^T {x^t​}t=1T​，其输出为每个时间步上的分类结果 { y t } t = 1 T \{y_t\}_{t=1}^T {yt​}t=1T​，判断输入序列是真实还是合成。判别器的更新过程亦可参考上述 LSTM 方程（将输入改为 $x_t$ 或 ${\hat{x}}_t$ 即可）。

为提升生成器的建模能力，RGAN-LS 采用了两种损失函数：对抗损失（adversarial loss）与矩匹配损失（moment matching loss）。
其中，对抗损失用于确保生成序列与真实时间序列之间无法被判别器区分。该损失函数定义为：

$${\mathcal{L}}_{adv}={\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x)]+{\mathbb{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$$

其中，$p_{data}$ 表示真实时间序列的分布，$p_z$ 表示潜在随机向量的分布。该损失函数驱动生成器不断生成越来越逼真的序列，使判别器难以分辨真假，从而提升生成数据的质量与真实性。

对抗损失在训练过程中起着关键作用，确保生成器 $G$ 所产生的合成时间序列在统计上与真实时间序列高度相似，有效实现高质量的多变量时间序列数据增强。

矩匹配损失与总损失函数

相较于对抗损失，矩匹配损失（moment matching loss）用于衡量真实与合成时间序列在均值（即一阶矩） 与方差（即二阶中心矩） 上的相似性。该损失项鼓励生成器生成具有与真实时间序列相似统计特征的合成序列。

矩匹配损失 ${\mathcal{L}}_{mm}$ 定义如下：

$${\mathcal{L}}_{mm}=\frac{1}{T}\sum _{t=1}^T\Vert {\mu }_{x,t}-{\mu }_{G(z),t}{\Vert }_2^2+\frac{1}{T}\sum _{t=1}^T\Vert {\sigma }_{x,t}-{\sigma }_{G(z),t}{\Vert }_2^2$$

其中，$\mu$ 与 $\sigma$ 分别表示时间序列的均值与标准差。矩匹配损失通过对齐统计矩来弥补生成数据与真实数据之间的差异。均值体现了监测变量的平均趋势，而方差则衡量其波动范围，反映其偏离平均值的程度。

通过最小化真实与合成时间序列在均值与方差上的差异（如公式所示），生成器能够输出更贴近真实统计特征的时间序列数据。

最终，提出的 RGAN-LS 网络通过组合对抗损失与矩匹配损失进行训练。整体训练目标函数定义如下：

$${\mathcal{L}}_{\text{RGAN-LS}}={\alpha }_0{\mathcal{L}}_{adv}+{\alpha }_1{\mathcal{L}}_{mm}$$

其中，${\alpha }_0$ 与 ${\alpha }_1$ 为标量权重系数，用于调节两类损失在训练过程中的相对重要性。该加权损失函数在保持样本质量的同时确保统计特征对齐，从而实现对抗学习与统计一致性的双重优化。

---

2.2 实现流程

图 2 展示了预测滑坡位移的四阶段流程。针对三峡库区存在阶跃形变的滑坡，累计位移被分解为趋势项与周期项，分别预测后再组合。趋势位移的预测相对简单，精度高；而周期位移受多种触发因素影响，预测难度较大，因此需要复杂的机器学习模型辅助。

为此，本文提出的 RGAN-LS 数据增强方法被用作上游数据处理手段，以提高周期位移预测的准确性。

---

2.2.1 第一步：位移分解

已有研究（Liu 等, 2020；Yang 等, 2019）指出，水库滑坡的累计位移时间序列可通过如下公式分解为趋势项与周期项：

$$S=f+j$$

其中，$S$ 表示累计位移，$f$ 为趋势项，$j$ 为周期项。最终的预测位移由趋势与周期预测值相加得到，实现趋势演化与周期响应的独立建模。

趋势项的提取使用 Hodrick-Prescott 滤波器（Zhu 等, 2017），该方法通过对时间序列平滑操作最小化波动性，从而提取平滑趋势。滤波器中的平滑参数依据周期性设定，若数据存在年度周期性，标准平滑系数为 $100$。

---

2.2.2 第二步：趋势位移预测

趋势项预测采用双指数平滑法（Double Exponential Smoothing, DES）。该方法适用于带有平稳趋势的时间序列数据，通过两层指数平滑操作实现预测：一层平滑原始观测值 $x_t$，另一层估计趋势 $b_t$。

其一阶预测 $F_{t+1}$ 定义如下：

$$\begin{array}{rl}{F}_{t+1}& =s_t+b_t\\ s_t& =\alpha x_t+(1-\alpha )(s_{t-1}+b_{t-1})\\ b_t& =\beta (s_t-s_{t-1})+(1-\beta )b_{t-1}\end{array}$$

初始条件：

$$s_1=x_1,b_1=x_1-x_0$$

其中，$\alpha \in (0,1)$ 与 $\beta \in (0,1)$ 为平滑系数，通常通过最小化均方根误差（RMSE）利用最小二乘法进行优化。

---

2.2.3 步骤3：周期性位移预测

2.2.3.1 特征选择

周期性位移受到诱发因素（如降雨、水库水位）以及历史位移所产生的滞后效应影响。根据前人研究（Liu 等, 2020；Li 等, 2021b；Ge 等, 2023），选取了 12 个诱发因素及其滞后项作为候选模型输入（见表 1）。

然而，若使用所有候选变量，可能会引入与周期位移低相关的变量，增加噪声并降低模型性能。为识别最优输入特征，使用 最大信息系数（MIC） 方法评估候选特征与周期位移之间的相关性，仅保留 $MIC\ge 0.3$ 的变量（Wang 等, 2023b）。此外，还使用 偏自相关函数（PACF） 选择周期项的最优滞后阶数，依据其 $|PACF|$ 值（其中 $n$ 表示样本数量）。

---

2.2.3.2 数据增强

本文提出的 RGAN-LS 模型 用于生成诱发因素（如降雨、水库水位）以及周期性位移的合成时间序列。生成器以从均匀分布采样的潜变量为输入，输出时间序列；判别器用于判别生成数据与真实数据的差异。
RGAN-LS 的训练目标由两个部分组成：对抗损失 $L_{adv}$ 和 矩匹配损失 $L_{mm}$，定义如下：
对抗损失和矩匹配损失的加权总目标为：

$$L_{RGAN-LS}={\alpha }_0{L}_{adv}+{\alpha }_1{L}_{mm}$$

其中 ${\alpha }_0$ 和 ${\alpha }_1$ 为可调权重，用于平衡生成数据的个体质量与统计特性。
RGAN-LS 最大训练周期为 20,000 次。在训练过程中，进行参数搜索（详见表 2）以确定最佳超参数组合。
为评估生成数据的质量，引入 最大均值差异（MMD） 指标，用于衡量真实数据分布 $P$ 与生成数据分布 $Q$ 之间的差异。其基于径向基函数（RBF）核的定义如下：

$${\text{MMD}}^2(P,Q)=\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^{n}k(p_i,p_j)+\frac{1}{m(m-1)}\sum _{i=1}^m\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^{m}k(q_i,q_j)-\frac{2}{nm}\sum _{i=1}^n\sum _{j=1}^{m}k(p_i,q_j)$$

其中 $k(\cdot ,\cdot )$ 为 RBF 核函数，$n$ 和 $m$ 分别为 $P$ 和 $Q$ 中的样本数。

选择 MMD 值最小的生成器用于下游数据增强任务。训练集为特征选择前的原始多变量数据，包含水库水位、降雨与周期性位移，序列长度为 12 个月，因此生成器输出的时间序列同样包含这三项。为进行下游滑坡位移预测，可根据表 1 中已选特征计算得到对应输入，构建适用于 ML 模型训练的数据集。

---

2.2.3.3 机器学习算法

本文选取两类机器学习模型进行对比验证数据增强效果：PSO-SVM 和 LSTM。

---

（1）PSO-SVM

支持向量机（SVM）将输入空间中的数据映射到高维特征空间中，寻找最优分类超平面。其泛化能力强，且参数调节较少，常采用 径向基函数（RBF）核函数。

SVM 模型的性能受以下参数影响较大：

• 惩罚因子：$C$
• 非敏感损失函数：$\epsilon$
• 核函数带宽：$\gamma$

使用 粒子群优化算法（PSO） 搜索最优参数组合。PSO 中每个粒子表示一个候选解，具有位置、速度与适应度。

模型训练采用 五折交叉验证 进行性能评估。

---

（2）LSTM

LSTM 是一种适用于时间序列建模的动态循环神经网络（RNN），能有效捕捉长期依赖关系。

其结构包括：

• 输入层
• 一个或多个隐藏层（含记忆单元）
• 输出层

每个记忆单元包含：

• 输入门
• 遗忘门
• 输出门

这些门控制信息的输入、保留与输出，允许模型有效学习时间序列中的动态演化模式。

LSTM 性能受以下超参数影响：

• 隐藏层数
• 每层神经元数
• 学习率

使用 网格搜索法调参以获取最优组合。

---

为提高预测精度与鲁棒性，所有模型采用一步预测策略（One-step-ahead prediction），即每次只预测下一个时间点，并基于最新数据持续更新预测结果。这种策略可增强对当前趋势的响应能力，降低多步预测中误差的累积效应。

---

2.2.4 步骤 4：模型评估

为了评估机器学习模型在滑坡位移预测中的性能，采用了 均方根误差（RMSE） 和 平均绝对误差（MAE） 作为评价指标。较低的 RMSE 和 MAE 值表示模型具有更好的预测性能。这两个指标定义如下：

$$\text{RMSE}=\sqrt{\frac{1}{l}\sum _{i=1}^l(y_i-{\hat{y}}_i{)}^2}$$

$$\text{MAE}=\frac{1}{l}\sum _{i=1}^l|y_i-{\hat{y}}_i|$$

其中，$y_i$ 和 ${\hat{y}}_i$ 分别表示实际观测值和预测的滑坡位移值，$l$ 表示数据点的数量。

考虑到机器学习模型在预测周期项时存在的随机性，每种算法独立运行 100 次，无论是否使用基于 GAN 的数据增强方法。随后计算对应的 RMSE 和 MAE 值，采用评价指标的 最优值和平均值 分别评估各算法的最佳与平均预测性能。

---

3. 数据与材料

降雨和水库调度（年调节水位差达 30 米） 显著影响了三峡库区大量岸坡的稳定性（Tang 等, 2019；Chen 等, 2023）。受降雨和水库活动诱发的滑坡（如Baishuihe滑坡和Shuping滑坡）表现出明显的 阶梯状变形特征。本文以这两个滑坡为例，用以展示和验证所提出的方法。

对于两个滑坡，最近两年的数据作为测试集，其余数据用于训练。这一划分的依据如下：

1. 控制测试集占比在合理范围（20%-30%）；
2. 保留两完整水文年及其对应的阶梯形变，用于测试。

---

3.1 Baishuihe滑坡

Baishuihe滑坡位于长江南岸（图 3a），距三峡大坝约 56 公里。该滑坡为大型厚层土质滑坡，长 600 m、宽 700 m、厚 30 m，体积约 $12.6\times 10^6$ m³。滑体由第四纪沉积物组成，包括粉质黏土和结构紊乱的块石；基岩主要为侏罗系香溪组的粉质泥岩与含泥粉砂岩。

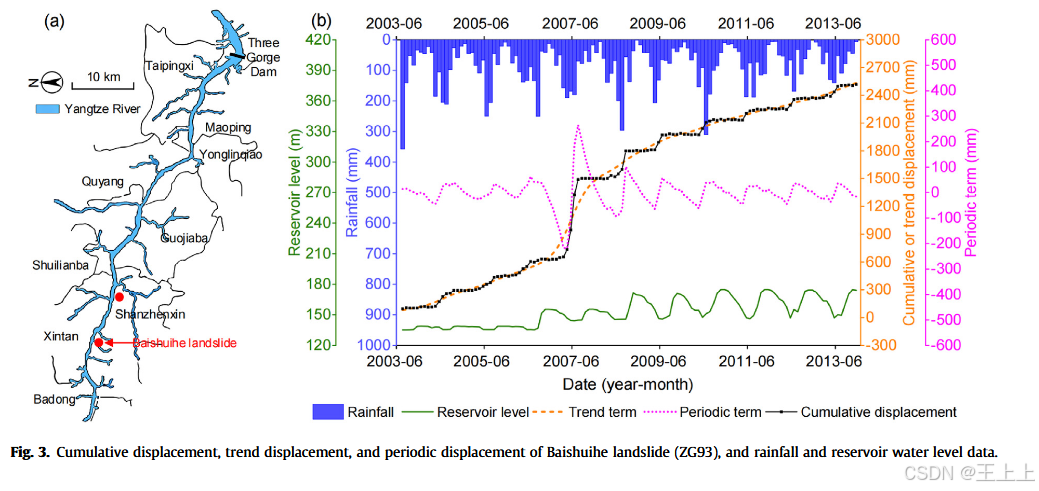
地表变形主要发生在滑坡边界和前缘，伴随张裂缝的发展。2003 年首次蓄水后出现初始裂缝。横向裂缝的发展和滑坡区房屋损坏导致 85 名居民搬迁。

滑坡活动区内的 GPS 站点 ZG93 表现出显著的变形模式、较长的位移时间序列和高位移量，是位移分析的典型代表。图 3b 展示了 2003–2013 年的累积位移、降雨和水位观测数据，以及 Hodrick-Prescott 滤波分解的趋势与周期分量。

Baishuihe滑坡的变形与三峡水位变化相关，可分为三阶段：

• 阶段 I（2003–2006）：尽管水位变化较小（135–140 m），监测点依然表现出平稳、阶梯状的位移增长，主要出现在水位下降期；
• 阶段 II（2006–2008）：2007 年首次出现 155 m 降至 145 m 的水位骤降，导致水动力压力增大和渗流变化，ZG93 位移瞬间增加超过 800 mm；
• 阶段 III（2008–2013）：尽管降雨量达 626.4 mm，但首次水位从 175 m 降至 145 m 时的最大月位移仅为 98.9 mm。此后，年位移仍在每年汛期呈阶梯状增长，但每级增长幅度逐年递减。

---

3.2 Shuping滑坡

Shuping滑坡属于残积滑坡，位于沙镇溪镇，长江南岸（图 4a），距三峡大坝约 47 公里。滑坡体积约为 $27.5\times 10^6$ m³，厚度为 30–70 m。

滑体上部主要为含巨石和砾石的土体，下部为粘土与粉质黏土；底部基岩属巴东组，主要由紫红色粉砂岩与泥岩、泥灰岩互层组成。

Shuping滑坡在水库水位下降期间加速、回涨期间减速，这可能与滑体层间的渗透性差异有关（Seguí 等, 2020）。此外，当地持续性降雨也被视为潜在诱因。

有关地质背景与变形特征，详见 Wu 等（2019）研究。监测站点 ZG88 因其变形显著、数据丰富，被选为位移建模代表点。

图 4b 展示了 2006–2012 年间的累计位移、降雨与水位观测数据，以及趋势与周期分解。

从图中可见，Shuping滑坡自 2008 年起在汛期发生剧烈年变形，与高月降雨相一致。然而，值得注意的是，降雨可能并非加速的主因：

• 最大月降雨（约 300 mm） 出现在 2008 年 6/7 月与 2010 年 6 月，但对应位移跳跃量反而较小；
• 位移跳跃最大的年份（如 2009 和 2012 年）反而降雨量较小。

此外，水库水位上升期间的位移速率非常低（约 0–1 mm/d），而在水位下降期间迅速加速。自 2003 年以来，滑坡最大变形速率始终出现在 6 月水位下降的高峰期。因此，尽管强降雨伴随滑坡加速发生，但对比降雨和位移的数量级，表明其并非主因；库水位回落才是主加速因素。

---

除了位移外，这两个滑坡的数据集主要包含外部环境因素的时间序列。然而，在理解与预测滑坡动态时，岩土体的物理与力学性质也极为关键。由于缺乏这类参数的时间序列数据，将其纳入模型仍具挑战。

本研究致力于在三峡库区构建基于诱发因素响应的数据驱动位移预测模型，延续了此前研究（Cao 等, 2016；Huang 等, 2017；Zhou 等, 2018；Zhang 等, 2022b）。未来，随着监测技术的进步（Du 等, 2021；Liu 等, 2023；Ye 等, 2023），RGAN-LS 框架可进一步结合全面的岩土参数，提升预测能力。

---

4. 结果

4.1. 趋势位移预测

选择了监测站ZG93和ZG88，分别建立并评估了Baishuihe和Shuping滑坡的预测模型。在趋势位移预测过程中，DES参数$a$和$b$分别设置为0.99和0.98，以获得平滑的结果（Jiang等，2021）。图5显示，预测的趋势位移与现场测量结果非常接近。Baishuihe测试集的RMSE为0.75，MAE为0.65，而Shuping测试集的RMSE为3.96，MAE为3.4。

4.2. 周期性位移预测的输入变量

为了预测周期性位移，我们根据之前的研究识别了12个潜在的输入变量，具体列表见表1（详见2.2.3节）。这些变量考虑了触发因素（如水库水位及其变化、降雨量），以及演化状态（如先前的位移）。

图6展示了这12个输入变量与周期性位移之间的相关性。

图6显示，Baishuihe滑坡主要受过去两个月降雨量（输入8）和当前月水库水位变化（输入4）的影响。另一方面，Shuping滑坡主要受到过去两个月的平均水库水位（输入3）和过去两个月的降雨量（输入8）的影响。对演化状态因素的滞后顺序发现，影响最大的滞后为一和二，分别对应输入10和输入11。对于Baishuihe滑坡，除了输入6（当前月降雨量）和输入12（过去三个月的周期性位移）外，所有候选变量均被选择为输入，因为它们都超过了MIC和PACF的阈值。对于Shuping滑坡，只有输入12被排除。

4.3. 基于GAN的数据增强

4.3.1. RGAN-LS参数选择

经过参数搜索（详见2.2.3节），确定了基于Baishuihe滑坡数据的RGAN-LS模型的最优参数组合。该模型使用GRU的递归单元，批量大小为5，隐藏单元大小为16，单层，潜在维度为5，学习率为0.0001。Shuping滑坡的最优参数组合为：GRU递归单元，批量大小为5，隐藏单元大小为8，2层，潜在维度为3，学习率为0.0001。使用MMD评估生成器的性能，Baishuihe滑坡和Shuping滑坡的MMD值分别为0.25和0.17。这是所有训练过的RGAN-LS模型中最低的值。

4.3.2. 真实时间序列与合成时间序列的视觉比较

RGAN-LS生成的合成数据质量通过与真实多变量时间序列的视觉比较来评估。

图7和图8的上部分分别显示了从Baishuihe和Shuping滑坡中随机选择的真实时间序列。下部分则显示了通过训练的RGAN-LS模型生成的合成时间序列。

对于每个变量，从真实数据和合成数据中随机选择了10个序列。这些序列的长度为12个月，与RGAN-LS训练集的序列长度一致。

需要注意的是，真实时间序列与合成时间序列之间没有一一对应的关系。这是因为GAN模型的生成器会从潜在空间中随机抽样潜在变量，这可能会导致生成的新样本在真实数据集中并不存在（Goodfellow等，2014）。

然而，即使合成数据可能包含新样本，GAN模型旨在捕捉真实数据的潜在分布。合成数据应展现与真实时间序列相似的模式和分布，正如图中所示。包括水库水位、降雨量和周期性位移在内的多变量时间序列表现出复杂的时间模式。

举例来说，水库水位由于人为干预显示周期性和连续的波动，降雨量在干旱季节和雨季之间差异显著，在雨季有明显的增加，导致图中出现峰值。周期性位移受水库水位和降雨量的影响，导致相应的波动。合成样本在定性上与真实数据匹配，具有相似的周期性变化、峰值和波动。

图7和图8展示了RGAN-LS模型能够捕捉到Baishuihe和Shuping滑坡现场测量数据集中的某些模式和动态。

4.3.3. 真实时间序列与合成时间序列的定量评估

在本研究中，MMD被用来定量评估RGAN-LS模型的性能。MMD不仅用于评估在RGAN-LS模型训练中的合成数据质量，也是一种广泛认可的度量标准，用于将合成数据与真实数据集进行基准比较（Li等，2019，2023；Gnanha等，2022）。MMD衡量两个数据分布（例如真实数据和合成数据）在RKHS中的散度，如公式(3)所定义。通过估算这些数据集分布特征之间的距离，MMD有效地捕捉了相似度，反映了数据的潜在模式。

为了进一步评估所提出的RGAN-LS模型的性能，我们使用MMD与几种基准模型进行比较，如表3所示。

基准得分是通过将训练集的时间序列样本与测试集的时间序列样本进行比较得出的，后者是实际的时间序列数据（Koochali等，2023）。

该得分为每个数据集上可以实现的最优性能提供了经验基准。比较中使用的基准模型包括k最近邻（KNN）（Peterson，2009）和高斯混合模型（GMM）（Reynolds，2009）。

KNN方法通过平均k个最接近的数据点的特征来生成新样本，而GMM方法通过估计高斯分量的参数来代表数据的结构和分布。定量评估结果显示，所提出的RGAN-LS模型的MMD得分（得分越低越好）显著低于传统插补模型如KNN和GMM所得到的得分。

结果还表明，RGAN-LS生成的样本接近经验最佳值（即基准得分），在两个数据集上表明，合成数据准确地反映了真实数据的潜在分布。与传统插补方法相比，GAN具有显著优势，因为它们直接从数据中学习，而不依赖于关于数据分布的假设（如GMM）或预定义的簇和距离度量（如KNN）。

这使得GAN能够更灵活、适应性地捕捉数据的潜在模式和特征。通过对抗训练，GAN在合成样本的质量上实现了持续的反馈循环，相较于传统方法，取得了更优的性能。

GAN擅长生成逼真的合成时间序列数据，正是由于它们能够捕捉复杂的非线性模式和时间动态。在总结中，这些结果强调了RGAN-LS生成的合成时间序列在重要统计指标上与真实数据紧密匹配的能力。此外，结果还表明，RGAN-LS在传统插补技术上的优势。定量评估不仅验证了所提出的生成模型的有效性，还展示了其在后续预测任务中作为数据增强的潜力。

4.3.4. 合成数据与真实数据之间的变量相关性

在本节中，视觉上检查了多变量时间序列数据集中各特征之间的相关性。

图9和图10展示了联合图，直观地比较了真实数据和通过RGAN-LS模型生成的合成数据中不同变量对之间的相关性。

该图通过散点图及相应的边缘直方图展示了变量之间的配对关系。显然，合成数据准确地捕捉了真实数据中的相关性。

具体而言，合成数据展示了与真实数据相似的数据点分布和聚类情况。

边缘直方图显示，合成数据与真实数据中每个单独变量的分布形态和特征高度一致。

然而，重要的是要注意，在极端降雨情况下，尤其是超过300毫米时，模型的表现可能受到影响。这可以归因于训练数据中这些极端值的数据稀缺性，以及GAN在准确捕捉分布尾部（包含这些极端值）的固有挑战。总体而言，合成时间序列成功地捕捉了真实数据所表现的复杂时间模式，这在定性和定量评估中都有体现。所提出的RGAN-LS模型能够生成逼真的多变量时间序列数据，同时有效地捕捉时间依赖性。此外，它成功地保持了真实数据集中的变量之间的潜在相关性。因此，这进一步证明了RGAN-LS在数据增强方面的潜力，通过生成逼真的数据，提升了下游机器学习模型在滑坡位移预测中的表现。

4.4. 性能评估

4.4.1. 实验设置

使用了两种广泛应用的机器学习（ML）算法，LSTM和PSO-SVM，用于建立基于所选输入变量和多变量时间序列的周期性位移预测模型。最终的累积位移预测结果通过将基于ML的周期性位移预测结果与基于DES的趋势位移预测结果结合得到。

LSTM模型的网络架构包括两层隐藏层，每层后接一个dropout层，最后是一个全连接（密集）层作为输出。使用网格搜索来找到隐藏神经元的最优参数‘num_nodes’（40、60和80）和dropout率‘drop_rate’（0.1、0.2和0.3）。

PSO-SVM模型使用RBF内核。PSO-SVM的超参数搜索包括惩罚因子$C$（从1到100）、核函数参数$g$（从0.001到1）和损失函数参数$p$（从0.02到0.2）。PSO算法的进化代数为100，种群数量为20。这些范围是根据文献中的经验结果选择的（Zhou等，2016；Miao等，2018），旨在确保对参数空间进行全面探索，同时平衡模型复杂性与过拟合风险。

测试集由最后两年的观测数据组成，共24个数据点。因此，剩余的数据点，即Baishuihe滑坡的99个数据点和Shuping滑坡的58个数据点，用于训练目的。对于使用RGAN-LS进行数据增强的机器学习模型，增强比例设置为50%，即训练集大小的一半。需要注意的是，对于PSO-SVM模型，训练集大小等于用于训练的剩余数据点数，而对于LSTM模型，训练集由按时间窗口切分的序列组成。

4.4.2. 模型性能的经验评估

4.4.2.1. 案例1：Baishuihe滑坡

Baishuihe滑坡测试集的累积位移预测结果如图11和表4所示。为了应对固有的随机性，机器学习模型（无论是否使用基于GAN的数据增强）都分别运行了100次，以确保每个实验设置的稳定性。于是图11中预测区间的产生了（参见图11a、b、d和e）。

对于LSTM模型，图11a和图11b中的可比预测区间宽度表明，基准模型（即未进行数据增强的模型）和增强模型的稳定性相似。

然而，图11c中的平均预测曲线显示，增强模型的位移（实线黑色曲线），尤其是在每年位移快速增加的关键预警期（5月至8月期间），比基准模型表现得更加敏感。这些发现表明，增强模型能够更及时地响应触发因素，从而提高了在突变位移期间的预测能力。

从定量上看，表4中的RMSE和MAE指标显示，LSTM模型在数据增强下的平均性能和最佳单次性能均有显著提高（超过16%）。

对于PSO-SVM模型，图11d和图11e显示，增强PSO-SVM模型的预测区间明显宽于基准模型，表明输出的不稳定性更大。

此外，图11f中的平均预测曲线显示，增强模型的波动性较大。

从定量上看，表4中的RMSE和MAE指标表明，增强后的模型在均值准确度上的提升有限（分别为1.74%和7.14%），但在最佳单次预测准确度上有显著提升（分别为35.62%和35.96%）。

4.4.2.2. 案例2：Shuping滑坡

图12和表5展示了Shuping滑坡的累积位移预测结果。

与Baishuihe滑坡相比，Shuping滑坡的RMSE和MAE值较高，这可能归因于其更大的规模和更复杂的演化行为，这本身就对准确预测构成了挑战。此外，两者数据量的差异也起到了作用，Baishuihe滑坡由于数据集更丰富，因此有利于模型训练。与案例1相比，可以观察到相似的模式。

对于LSTM模型，增强模型和基准模型的预测区间宽度大致相等（图12a和图12b）。

然而，增强模型的平均预测曲线更接近监测曲线，如图12c所示。相比之下，对于PSO-SVM模型，增强模型的预测区间显得更宽（图12d和图12e），但两种模型的平均预测曲线几乎相同（图12f）。

RMSE和MAE的结果进一步表明，增强后的LSTM模型能够同时改善单次最佳预测和平均预测性能，这从表5中的统计值可以看出。增强后的PSO-SVM模型显著提高了单次最佳预测性能，RMSE最大提高了15.84%。然而，平均预测性能的变化较小，RMSE仅增加了3.53%，MAE则减少了3.91%。

此外，尽管两种滑坡案例的结果一致，但数据增强对Shuping滑坡位移预测性能的提升通常小于Baishuihe滑坡。**这可能是由于Shuping滑坡的数据样本量较小，相较于Baishuihe滑坡，Shuping滑坡的训练数据有限，从而限制了RGAN-LS模型学习数据分布的能力。**因此，通过增强数据获得的性能提升在Shuping滑坡上较Baishuihe滑坡要小。

总体而言，数据增强的LSTM模型展示了更强的响应能力，尤其是在滑坡变形的突变阶段。它在最佳预测准确度上有显著提高，并且相比基准模型整体表现更加优越。无论是单次最佳表现还是平均表现的一致性提升，都表明了该模型的鲁棒性和稳定性。另一方面，尽管数据增强的PSO-SVM能够产生更好的单次最佳预测，但其不稳定性增加，抵消了这些优势，如更宽的预测区间、平均曲线的波动性增大以及均值性能的边际提升所示。建议使用基于GAN的数据增强可能会增加SVM模型的方差，导致偶尔性能提升，但并未带来一致的改进。

5. 讨论

前面的分析已经证明，采用生成性人工智能方法进行训练数据增强能够提升滑坡位移预测的性能。具体而言，RGAN-LS生成的合成样本数量对模型性能有显著影响。为了进一步探讨这一问题，我们进行了一个基于Baishuihe滑坡数据集的案例研究，并分析了不同合成与真实样本大小比率对预测结果的影响。我们评估了合成与真实样本大小比率为25%、50%、75%、100%、150%和200%的情况。25%的比率表示合成样本数量为真实样本数量的25%。在不同的比率下，我们使用相同的机器学习算法——LSTM和PSO-SVM，并进行数据增强。每个模型在100次独立运行后的性能结果展示在图13和图14中。

图13显示，增强后的LSTM模型的RMSE和MAE在比率从25%增加到50%时首先下降，然后在比率从50%增加到200%时上升。**Baishuihe滑坡的最佳合成样本比率大约为50%，此时模型的平均预测误差最小。**与基准模型（无数据增强）相比，结果表明，基于GAN的数据增强可以有效提升所有比率下的模型性能。此外，当使用RGAN-LS生成的合成样本，且比率范围为25%到100%时，LSTM模型的性能显著提高，这通过不重叠的95%置信区间得以体现，表明统计上显著。然而，在150%和200%的比率下，性能提升较为边际。

图14显示，基于GAN的数据增强未能有效提高静态PSO-SVM预测模型的性能。

增强模型在25%和50%的比率下，平均RMSE和MAE值略低于基准模型。然而，更宽的置信区间表明预测不确定性显著增加。随着合成与真实样本比率的进一步增加，使用合成样本增强真实数据会持续导致模型性能退化，相比基准模型表现更差。超过最佳比率后性能下降，表明过多的合成数据可能对模型产生不利影响。我们推测，模型在最佳比率之后性能下降的原因是过拟合到合成数据。尽管合成数据对于训练有价值，但它们可能无法充分捕捉真实数据分布的复杂性。因此，模型可能失去对新、未见数据的泛化能力，导致RMSE和MAE增加。

总之，所提出的RGAN-LS网络显著提升了动态LSTM模型的性能，而在使用生成方法时，静态SVM模型并未表现出类似的性能提升。SVM和LSTM模型在RGAN-LS数据增强下的性能差异可以归因于它们固有的架构差异（Xing et al., 2019；Yang et al., 2019）。

基于RNN构建的RGAN-LS擅长捕捉时间序列中的时间相关性。LSTM是专门设计用来利用这些时间动态的，因此它从这种增强中受益，特别是在预测任务中。相比之下，像SVM这样的静态模型缺乏处理时间序列数据所需的时间处理能力，无法充分利用RGAN-LS增强的优势。值得注意的是，在数据增强之前，SVM模型的平均RMSE/MAE值低于LSTM模型。这可能是由于LSTM在将样本拆分成子序列后，相比PSO-SVM，样本量较小。使用RGAN-LS网络进行数据增强后，LSTM的表现优于PSO-SVM，证明了该生成方法可以捕捉时间序列数据的时间相关性，并在数据有限的情况下充分利用动态模型的预测潜力。

这些发现突出了数据增强技术与模型架构对齐以最大化性能提升的重要性。

局限性

尽管所提出的RGAN-LS网络为滑坡位移预测的数据增强提供了一种有前景的方法，但本研究也存在一些局限性。

首先，训练GAN模型往往非常困难。GAN的训练通常需要广泛的超参数调整，因为即使是批量大小、学习率和网络架构等参数的微小变化，也可能显著影响模型性能和稳定性。 因此，在本研究中，我们进行了超参数网格搜索，以找到最佳参数配置的生成器。

此外，评估GAN模型的性能，特别是合成样本的质量，可能是具有挑战性的。在本研究中，采用了MMD作为定量评估指标来评估RGAN-LS的性能，这在之前的研究中得到了广泛应用（Borji, 2019）。**然而，定量评估生成样本的质量仍然是GAN研究中的一个开放问题。**未来的研究可以考虑使用其他评估指标，如Kullback-Leibler散度（KLD）和Jensen-Shannon散度（JSD），以进一步了解GAN的性能。像本研究中探索的那些超参数调整策略和定量评估指标对于开发可靠和有效的生成模型进行数据增强至关重要。

此外，所提出的模型在**合成极端值（如案例研究中的极端降雨）**方面存在一定的局限性。这主要是由于训练数据中极端值的稀缺，以及模型在捕捉分布尾部方面的挑战。未来的研究可以通过引入有针对性的过采样技术、优先考虑极端值的特殊损失函数以及利用条件GAN来增强模型性能。

根据之前的分析，虽然实施RGAN-LS模型相较于没有数据增强的ML模型需要更多的计算资源和时间成本，但基于GAN的数据增强的好处可能会超过时间和计算资源的成本，因为生成的合成数据显著提高了模型性能，正如我们案例研究中所展示的那样。

GANs优势

生成性人工智能方法，如GANs，具有在各种数据挖掘任务中提供显著益处的潜力，超越了本研究中的应用场景。此外，GANs可以通过考虑数据噪声的影响来改善滑坡位移预测的区间预报，通过生成合成训练数据，生成更稳健的模型。GANs还可以通过生成合成数据来增强地质灾害异常检测，帮助训练判别网络，提高其区分正常行为和异常行为的能力。这提高了异常检测系统的准确性和稳健性，特别是在异常数据稀缺时。在遥感领域，GANs可以通过过滤掉无关噪声和生成高保真合成图像来帮助提高图像分辨率和质量。这有助于克服稀疏或不完整数据集带来的限制，能够更准确地进行预测。未来的研究可以探索GANs在提升区域地质灾害评估中的潜力。

6. 结论

本研究提出了一种新型生成对抗网络（GAN），即RGAN-LS，用于通过增强有限的现场测量数据，提高机器学习模型在滑坡位移预测中的表现。

RGAN-LS利用递归神经网络（RNN）捕捉多变量时间序列数据中的复杂时间相关性，并采用定制的对抗损失和矩匹配损失函数，生成模拟真实数据特征的合成样本。定性和定量评估表明，RGAN-LS成功地再现了现场测量数据的时间动态和相关性。

随后，合成样本被用于增强LSTM和PSO-SVM模型的训练，以预测滑坡位移。两种滑坡案例的结果显示，数据增强的LSTM模型显著提高了预测性能（包括最佳单次性能和平均性能）和响应能力（特别是在变形加速期），相比于基准模型。这凸显了所提出的生成方法在增强动态网络应用中的高效性，例如滑坡位移预测。

进一步分析揭示了一个最佳的合成与真实数据增强比率，以最大化性能提升。

相比之下，尽管在重复实验中最佳预测有所改善，但在静态PSO-SVM模型中，平均性能仅有边际提升。然而，必须承认本研究的一些局限性。例如，GAN的训练需要额外的计算成本，并且需要仔细的超参数调整才能实现最佳性能。此外，评估合成数据的质量，特别是使用定量评估指标，仍然是一个挑战。未来的工作可以探索更多的评估指标，以进行更全面的评估。

总之，本研究提出了一种新型的数据增强框架，旨在解决滑坡位移预测中数据稀缺的关键挑战。通过RGAN-LS生成逼真的合成训练样本，可以增强数据驱动模型的预测性能，为在数据有限的情况下利用机器学习模型进行滑坡预测提供了有前景的解决方案。

生成性人工智能方法，如GANs，扩展了数据驱动模型在地质灾害管理中的能力。它们通过生成合成数据来提高模型准确性，从而增强预警系统。此外，它们在未来研究中为多种应用提供了潜在的利益。

问题

论文中 是先合成数据 再利用GRU训练吗?

是的，论文中确实是先利用RGAN-LS模型合成数据，然后再使用GRU（门控循环单元）或其他机器学习模型（如LSTM和PSO-SVM）进行训练。具体过程如下：

1. 合成数据生成： 首先，使用RGAN-LS模型，通过生成对抗网络（GAN）生成与实际滑坡数据相似的合成数据。这个过程通过RGAN-LS中的递归神经网络（RNN）部分来捕捉多变量时间序列数据中的时间相关性，并利用定制的对抗损失和矩匹配损失函数生成与实际数据特征相似的合成样本。

2. 数据增强与模型训练： 然后，将生成的合成数据与实际数据结合，增强训练数据集。接下来，使用GRU（或LSTM）模型，结合这些增强的数据进行训练，以提高预测性能，尤其是在数据稀缺的情况下。

3. 模型评估： 最后，通过不同的滑坡案例对比训练后的GRU（或LSTM）模型，评估其在位移预测中的表现，特别是比较数据增强后的模型和基准模型（没有使用数据增强）的性能。

因此，论文中的训练步骤确实是先通过RGAN-LS合成数据，然后用增强后的数据训练GRU或LSTM等动态模型。