【论文阅读18】-滑坡阶梯状位移预测-CNN+Bi-GRU+Attntion（2024-07）-CSDN博客

本文链接：https://blog.csdn.net/wangshangshang09/article/details/147201263

这篇论文主要探讨了使用深度学习模型预测滑坡位移的方法，特别是针对具有阶梯状曲线特征的滑坡位移。文章的重点在于介绍了一种新的混合模型——CNN-BiGRU-Attention，并通过与其他模型（CNN-BiGRU、CNN-BiLSTM、BiGRU-Attention、SMA-GRU、SMA-LSTM、SMA-SVM、GRU和LSTM）的比较，证明了该模型在滑坡位移预测中的优越性。

Meng S, Shi Z, Peng M, et al. Landslide displacement prediction with step-like curve based on convolutional neural network coupled with bi-directional gated recurrent unit optimized by attention mechanism[J]. Engineering Applications of Artificial Intelligence, 2024, 133: 108078.
基于卷积神经网络与注意力机制优化的双向GRU模型的滑坡阶梯状位移预测

期刊
《Engineering Applications of Artificial Intelligence》
JCR分区：Q1 （IF=7.5（2023年））
出版周期：双月刊（Bimonthly）
（EAAI）是由Elsevier出版的国际知名工程类学术期刊，创刊于1988年，专注于人工智能（AI）在各类工程领域中的实际应用。

作者介绍
第一作者：Shaoqiang Meng （R)
同济大学智能自主系统上海研究院
（自主智能无人系统全国重点实验室（同济大学））
通讯作者： Ming Peng（彭铭）
同济大学土木工程学院岩土工程系

模型介绍与优势：
- CNN-BiGRU-Attention 模型结合了卷积神经网络（CNN）用于提取空间特征，双向门控循环单元（BiGRU）用于捕捉时间相关性，并引入了注意力机制来突出重要信息。通过这种方式，模型能够更好地处理滑坡位移的空间和时间特征，从而提高预测精度。
- 该模型相较于传统模型（如GRU、LSTM）和其他混合模型（如CNN-BiGRU、CNN-BiLSTM等）表现出更高的准确性和鲁棒性。
趋势与周期位移预测：
- 论文指出，滑坡位移不仅包括周期性变化，还包括长期趋势变化。传统的预测方法往往忽略了趋势项的影响，而论文中的模型通过准确预测趋势位移和周期位移，显著提高了累计位移预测的精度。
突变位移预测的误差评估：
- 在滑坡位移的突变阶段，外部因素（如降水、地震等）可能导致滑坡发生突变，给预测带来挑战。论文提出了一种新的评估方法——非线性加权Huber损失函数（NLWHL），特别强调了突变状态下的误差，从而更精确地评估模型在突变位移预测中的表现。
与其他模型的比较：
- 论文通过与多种其他模型（如SMA-SVM、SMA-GRU、SMA-LSTM等）的比较，证明了CNN-BiGRU-Attention模型在准确度和鲁棒性方面的优势。通过R²、RMSE、MAE等指标，评估了各个模型在滑坡位移预测中的表现。
局限性与未来研究方向：
- 论文也指出了该方法的局限性，特别是深度学习模型的可解释性问题。未来的研究可以考虑开发更具可解释性的模型，并整合更多影响滑坡位移的因素（如地质条件、气象变化等）来提高模型的综合预测能力。

总之，本文通过提出CNN-BiGRU-Attention模型，展示了在滑坡位移预测中的应用潜力，并通过大量的实验与评估，证明了其在预测准确度和泛化能力上的优势。未来的研究可以进一步优化模型，增加更多的外部影响因素，提高预警系统的效果。

全文翻译

摘要

本研究旨在准确预测以阶梯状位移曲线为特征的滑坡位移，该类型位移源于多种因素的复杂交互作用，包括周期性与可变性因素。为此，我们提出了一种基于卷积神经网络（CNN）与注意力机制优化的双向门控循环单元（BiGRU）相结合的预测框架，用于预测具有阶梯特征的滑坡位移。

首先，利用自适应噪声的互补集合经验模态分解（CEEMDAN）算法将滑坡位移信号分解为周期项与趋势项。随后，构建CNN层以提取复杂的高维特征，同时搭建BiGRU层以捕捉历史序列中的时间依赖关系。值得注意的是，引入了注意力机制模块，以增强降雨、水位和历史位移数据中关键信息的影响力。

最后，提出非线性加权Huber损失函数（NLWHL）作为评估方法，用于衡量模型在突变状态预测中的准确性。结果表明，所提出的预测框架在滑坡位移预测精度方面优于其他智能算法。

针对总位移预测，CNN-BiGRU-Attention模型表现出更强的预测能力，在测试集上的RMSE值相比CNN-BiGRU、CNN-BiLSTM、BiGRU-Attention、SMA-GRU、SMA-LSTM、SMA-SVM、GRU和LSTM模型分别降低了12.52%、14.15%、15.58%、21.68%、21.84%、32.81%、58.10%和53.81%。

此外，引入NLWHL进一步突显了该框架在蠕变阶段与突变阶段预测中的卓越性能。对位移突变状态的有效识别，为早期预警与干预提供了关键契机。

关键词： 滑坡监测、白水河滑坡、自适应噪声互补集合经验模态分解、机器学习、深度学习、非线性加权Huber损失函数

1. 引言

水库滑坡
水库滑坡具有极强的破坏力，往往通过直接冲击或间接影响（如滑坡堰塞体、滑坡引发的涌浪等灾害链）造成严重的人员伤亡和财产损失（Gong 等，2021）。三峡水库的建设显著改变了区域的地质条件（Du 等，2012）。自2003年蓄水以来，三峡水库水位调节效应导致多处古滑坡重新活化（Tang 等，2019；Zhang 等，2023）。2003年，黔江坪滑坡复发，造成1200余人转移、14人死亡、10人失踪（Wang 等，2004）。当滑坡体进入水库时，可能产生巨大涌浪或形成堰塞湖，一旦溃决，将威胁航道安全、大坝及附属结构、周边船只以及上下游居民的生命财产安全。例如，2008年11月23日，龚家坊滑坡迅速滑入江中，产生巨大涌浪，并导致河道封堵近两天（Huang 等，2012）。

尤其值得注意的是，水库滑坡通常对外部触发因素更为敏感，如库水位波动和强降雨（Luo 等，2022；Pudasaini 和 Jaboyedoff，2020）。在库水位变化和降雨影响下，滑坡位移常表现为周期性阶梯式变化，具有长期响应特征（Glastonbury 和 Fell，2008；Lacroix 等，2020；Wang 等，2023b）。这种多因子相互作用导致的滑坡位移呈现出独特的阶梯状曲线，给预测带来了巨大挑战。

阶梯状滑坡特点
通常，阶梯状滑坡位移曲线被分解为周期项和趋势项，但以往研究多聚焦于周期项的预测，趋势项常被忽略（Yang 等，2023；Zhang 等，2020）。近年来，人工智能在遥感领域迅速发展（Hong 等，2023a, 2023b），基于数据驱动的机器学习方法在预测具有阶梯特征的周期性滑坡位移方面展现出良好表现（Xu 和 Niu，2018；Zhang 等，2019；Zou 等，2020a），能有效利用历史滑坡监测数据中的复杂非线性特征。

研究现状
Guo 等（2019）提出了反向传播神经网络（BPNN）用于阶梯状滑坡位移预测，但BPNN易陷入局部最优且收敛速度慢。为克服上述问题，Qing 等（2021）提出极限学习机（ELM），该方法在参数拟合方面表现优异，但在处理正向与反向序列关联分析方面仍需改进，且在深层训练中面临梯度消失与爆炸问题。Han 等（2021）采用支持向量机（SVM）进行位移预测，但模型剪枝不当容易导致过拟合。Gong 等（2022）结合支持向量回归与多算法优化技术，提出改进预测方案，有效缓解了过拟合问题。然而，这些研究大多将滑坡预测建模为静态回归问题（Zhang 等，2022b），忽略了输入数据之间的时间依赖关系。

存在问题
实际上，阶梯状滑坡位移具有典型的非线性动态特征（Yang 等，2019），且受地下水位与降雨等时变因素影响显著（Li 等，2018, 2019；Zhang 等，2021），这使得仅用静态模型难以准确预测滑坡位移。

引出GRU
为克服静态模型的不足，部分学者提出了动态模型。这类模型能够将输入特征的时间变化动态引入隐藏层，从而挖掘滑坡位移的时序变化规律（Zhang 等，2022a）。递归神经网络（RNN）曾用于滑坡预测等动态任务（Chen 和 Chou，2012），但在长序列学习中常因长期依赖问题而表现不佳。相比之下，长短期记忆网络（LSTM）可用于预测阶梯状滑坡位移（Yang 等，2019），但其结构复杂、参数量大，易导致计算成本高与过拟合。门控循环单元（GRU）则提供了一种更简洁高效的替代方案，能够克服LSTM的慢收敛问题（Xia 等，2021），更适合处理时间序列数据（Ubrani 和 Motwani，2019）。

GRU存在些许不足
然而，滑坡位移的预测不仅依赖时间因素，还需考虑降雨、水位和历史位移等多因子间的相互关系。静态模型由于缺乏层间连接，难以建立有效的时序关系；而尽管动态模型有所提升，仍未能充分挖掘影响因子间的深层次联系，限制了预测精度的进一步提高。因此，构建预测模型时，应特别重视多源特征的融合提取、长期依赖关系的建模以及关键信息的有效共享。

引出CNN用于提取特征
在特征提取与多因子时序数据融合方面，卷积神经网络（CNN）通过卷积与池化操作提取高阶特征，能有效减少人为特征提取中的误差（Nava 等，2023；Wu 等，2022）。双向门控循环单元（BiGRU）作为GRU的改进型，具备较强的时序特征提取能力，已广泛用于碳价预测（Wang 等，2021）、负荷预测（Kuster 等，2017）等领域，表现出较高精度。但在处理过长时间序列时，BiGRU仍存在信息丢失风险（Cinar 等，2018）。

引出注意力机制
注意力机制可作为一种资源分配机制，通过为输入特征赋予不同权重，突出关键特征信息，在避免长序列信息丢失的同时，提升模型对长期依赖的学习能力（Niu 等，2021）。

综上，准确预测阶梯状滑坡位移需综合考虑输入特征的动态时变特性、降雨、水位与历史位移等影响因子之间的关系，并从长序列中获取关键信息。但现有预测模型在这方面仍存在不足。此外，以往研究多忽略对趋势项的预测，而趋势项对滑坡响应具有重要意义。在预测包含蠕变与突变阶段的阶梯状滑坡位移时，突变状态的预测误差评估同样不可忽视，但这一问题常被忽略。

本文工作
为此，本文提出一种引入注意力机制优化的CNN-BiGRU模型，用于预测包含周期项与趋势项的阶梯状滑坡位移。该模型首先使用CEEMDAN算法对滑坡位移进行分解。本文的主要贡献如下：

提出一种基于注意力机制优化的CNN-BiGRU模型用于阶梯状滑坡位移预测。CNN用于提取分层特征结构，BiGRU用于捕捉时间依赖关系，注意力机制进一步聚焦于降雨、水位与历史位移中的关键信息，并为每个任务分配BiGRU隐藏状态，从而提高预测效率。
为验证模型有效性，本文将其与静态单模型（GRU、LSTM）、静态混合模型（SMA-SVM）、动态混合模型（SMA-GRU、SMA-LSTM）以及多种深度学习混合模型（CNN-BiGRU、CNN-BiLSTM、BiGRU-Attention）进行对比。SMA（黏菌算法）是一种启发式优化算法，用于优化模型参数、结构或训练过程，从而提升单模型性能。模型性能通过MAPE、RMSE、MAE、R²等指标评估。结果显示，所提模型预测误差更小，可靠性更高。
为更全面评估模型在预测阶梯状滑坡位移（尤其是突变状态）方面的性能，本文引入一种新型的误差评估方法——非线性加权Huber损失函数（NLWHL），以更关注突变状态下的预测误差。

接下来的章节结构如下：第2节介绍阶梯状滑坡位移的预测方法；第3节分析研究区滑坡位移数据的特征；第4节对所提CNN-BiGRU-Attention模型的预测结果与其他模型进行对比分析；第5节讨论模型的优势与局限性；第6节为本文结论部分。

2. 方法

2.1. 所提方法的框架

图1展示了本文所提出方法的整体框架，主要包括以下几个关键步骤：
在这里插入图片描述

（i）数据预处理：首先，采用CEEMDAN方法对滑坡累计位移进行分解，得到周期项与趋势项。此外，考虑到诱发因素存在滞后效应，将平均降雨量和平均水位与其他诱因一同考虑。诱发因素的选择依据灰色关联分析（GRA）和偏自相关函数（PACF）算法确定。

（ii）CNN-BiGRU-Attention模型构建：将滑坡位移数据划分为训练集和测试集。趋势位移与周期位移的训练数据分别输入CNN-BiGRU-Attention模型中，通过多次迭代确定预测精度最优的模型。该模型通过构建CNN层提取复杂高维特征，利用BiGRU层捕捉历史序列中的时间依赖性，特别地，引入注意力机制模块以增强关键特征的影响。

（iii）验证结果分析：随后，使用该模型对测试集进行预测。根据时间序列分析方法，对周期位移与趋势位移的预测值进行求和，以获得累计位移的预测结果。通过将预测结果与实测数据对比，评估模型的预测准确性。

（iv）模型性能评估：采用四种统计指标对模型预测精度进行量化分析，即均方根误差（RMSE）、平均绝对百分比误差（MAPE）、平均绝对误差（MAE）、相关系数（ $R^2$ ）以及运行时间。为更加准确评估模型在突变状态下的预测能力，本文引入一种新的非线性加权Huber损失函数（NLWHL），用于专门评估突变状态下的预测误差。

2.2. 数据预处理

2.2.1. 时间序列分解

滑坡累计位移随着时间呈现增长趋势，属于非平稳时间序列。这种位移变化主要受内部地质条件、重力载荷及外部因素如水压力变化等驱动。其中，水压力受降雨与水库水位季节性变化的影响，导致位移具有显著的波动性。为了便于分析，采用时间序列分析方法将滑坡位移分解为趋势项与周期项，如式（1）所示：

$\sigma(t) + \omega(t) \tag{1}$

其中， $t$ 表示时间， $L (t)$ 为滑坡累计位移， $\sigma(t)$ 为趋势项， $\omega(t)$ 为周期项。

经验模态分解（EMD）方法适用于分析和处理非线性、非平稳信号，可将信号按时间尺度特征进行分解（Huang et al., 1998）。但EMD在特征尺度上难以有效区分不同模态成分。为解决此问题，集合经验模态分解（EEMD）（Yeh et al., 2010）在整个时频域中引入白噪声，较好地解决了模态混叠问题。然而，白噪声的引入较为困难，且其分解过程效率不高，噪声消除存在一定问题。因此，本文采用完全集合经验模态分解（CEEMDAN）（Torres et al., 2011），该方法在每个阶段自适应地添加高斯白噪声，有效克服了EMD中的模态重叠问题，并解决了EEMD中的效率与噪声消除困难。

其具体操作步骤如下：

Step 1. 向待分解信号 $x (t)$ 添加均值为0的高斯白噪声共 $K$ 次，构造待分解序列 $x_i(t)$ ，共进行 $K$ 次实验，其中 $i = 1, 2, 3, ..., K$ ：

$x_i(t) = x(t) + \varepsilon \delta_i(t) \tag{2}$

Step 2. 对上述得到的序列 $x_i(t)$ 进行EMD分解，获取第一个本征模态函数（IMF），多个IMF的均值作为CEEMDAN得到的第一个IMF分量：

$\text{IMF}_1(t) = \frac{1}{K} \sum_{i=1}^{K} \text{IMF}_{i1}(t) \tag{3}$

随后计算第一个残差项：

$r_1(t) = x(t) - \text{IMF}_1(t) \tag{4}$

Step 3. 对第 $j$ 次分解后的残差信号，添加特定噪声后继续进行EMD分解：

$\text{IMF}_j(t) = \frac{1}{K} \sum_{i=1}^{K} E_1 \left[r_{j-1}(t) + \varepsilon_j E_j^{(1)}(\delta_i(t))\right] \tag{5}$

然后更新残差：

$r_j(t) = r_{j-1}(t) - \text{IMF}_j(t)$

Step 4. 当EMD满足停止条件且第 $n$ 次分解的残差信号 $r_n(t)$ 呈现单调特征时，迭代停止，CEEMDAN算法的分解过程结束。

2.2.2. 输入变量表征

具有阶梯形曲线的滑坡周期项，受到多种因素的复杂影响，例如水库水位、降雨量及历史位移（Ma 等, 2022；Wang 等, 2019；Xing 等, 2020）。此外，水库水位、降雨量与滑坡位移之间存在明显的滞后效应（Han 等, 2021；Wei 等, 2019）。因此，构建一个有效的预测模型需考虑多个输入变量，包括降雨、水库水位、水位变化量以及前期位移（Zhang 等, 2021；Zhu 等, 2017）。在本研究中，这些变量被视为潜在候选变量，如表1所示。

然而，并非所有与滑坡位移有关的变量都适合作为预测输入变量。与位移相关性较弱的变量可能引入噪声，降低预测精度（Huang 等, 2017）。因此，必须对候选变量与滑坡位移之间的相关性进行严格的定量评估，以筛选出强相关的变量，并剔除弱相关变量。

输入变量的质量对模型性能至关重要。本研究中，输入变量的筛选基于灰色关联分析（GRA） 原理。GRA通过对因素之间发展趋势的相似性与差异性进行量化评估，来衡量各变量之间的关联度。GRA值范围为 $[0, 1]$ ，值越高表示变量与滑坡位移的关联越强。

同时，引入了最大信息系数（MIC）以进一步筛选关键输入变量。MIC值越高，说明候选变量与滑坡位移之间的非线性相关性越强。本文设定MIC阈值为大于0.5，以确保仅选择与滑坡位移强相关的变量。

此外，还采用了偏自相关函数（PACF） 方法来确定时间序列的最优滞后阶数。该方法用于揭示周期位移预测中潜在的时间延迟结构。

2.3. CNN-BiGRU-Attention模型

本研究采用 CNN-BiGRU-Attention 模型来完成对滑坡阶梯形位移的特征提取与预测任务。CNN相较于传统神经网络，具有更广的感受野和权重共享机制，能有效应对滑坡位移时间序列中的非线性与随机特征。通过层间权重共享机制，CNN在降低复杂度与参数数量的同时，使用卷积核提取关键空间模式，是进行时间序列特征提取的有力工具。

为了进一步优化CNN提取的时域特征，引入了双向门控循环单元（BiGRU） 模型。与传统RNN相比，GRU结构更能有效缓解梯度消失问题。BiGRU的隐藏层包括正向与反向两部分，能够结合时间序列的正向与反向信息，增强对位移变化趋势的捕捉。隐藏状态通过正向与反向隐藏层状态的加权组合获得。

该模型结构如图2所示。为了更全面地介绍CNN-BiGRU-Attention模型，接下来的各节将依次说明CNN层（第2.4.1节）、BiGRU层（第2.4.2节）和注意力机制（第2.4.3节）。
在这里插入图片描述

2.3.1. CNN层

CNN在特征提取与整合方面表现出强大能力，能够捕捉滑坡诱因间的复杂关联关系，有助于提升位移预测精度。CNN由卷积层、池化层和全连接层组成（Selvaraju 等, 2019；Yao 等, 2020），如图3所示。
在这里插入图片描述

CNN的核心优化依赖于随机梯度下降（SGD） 与权重共享机制。卷积计算过程如下：

$\text{Conv}^f_i[j] = \left( \sum_{k=0}^{K_i} \omega^f_{ki} S_j[j + k] + b^f_{ki} \right) \times F \tag{6}$

其中， $\text{Conv}^f_i[j]$ 表示第 $l$ 层中第 $j$ 个神经元的输出， $F$ 为非线性激活函数， $b^f_{ki}$ 为偏置项， $S_j$ 为选定输入映射之一。

对于最大池化层（Maxing Layer），当池化大小为 $\times MP$ 时， $\text{Conv}^f_i[j]$ 的维度变为 $\times (L_i - K_i + 1) \times F_i)$ ，其计算表达式如下：

$\max \left\{ \text{Conv}^f_i \right\}_{1 \times (L_i - K_i + 1)}^{MP \times f_i} \tag{7}$

最大池化层输出的神经元表达为：

$S^{l+1}_i = f \left( u^l_j + \sum_{i \in M_j} \text{con}(v^l_{1ij}, x^l_{1i}) \right) \tag{8}$

这些操作构成了CNN的基本计算流程，帮助模型从输入数据中提取关键特征，提高滑坡位移预测的效果。

2.3.2. BiGRU层

为了进一步捕捉CNN提取的特征向量中的时间信息，并揭示滑坡历史位移的周期波动特征，本文引入了BiGRU模型。GRU属于递归神经网络（RNN）的一种，擅长处理时序特征。它将输入门与遗忘门合并为一个更新门，将状态与隐藏状态集成，简化结构的同时保留强大的时间记忆能力。

GRU的核心由两个门控机制构成：重置门 $r_t$ 与更新门 $u_t$ ，其数学公式如下：

$r_t = \sigma(W_r \cdot [h_{t-1}, x_t] + b_r) \tag{9}$

$u_t = \sigma(W_u \cdot [h_{t-1}, x_t] + b_u) \tag{10}$

$\tilde{h}_t = \tanh(W \cdot [r_r \odot h_{t-1}, x_t]) \tag{11}$

$h_t = (1 - u_t) \odot h_{t-1} + u_t \odot \tilde{h}_t \tag{12}$

其中， $\tilde{h}_t$ 为新记忆， $h_t$ 为最终输出状态； $W$ 和 $b$ 分别为权重矩阵与偏置项； $\sigma$ 和 $\tanh$ 为非线性激活函数； $\odot$ 表示矩阵点乘操作。

然而，传统GRU只能利用历史信息，无法获取未来信息。考虑到当前位移不仅与过去状态相关，还受未来影响，本文采用了双向GRU（BiGRU）。如图4所示，BiGRU综合考虑了时间正向与反向的序列关系，增强了模型对位移特征的表达能力。
在这里插入图片描述

BiGRU中时间点 $t$ 的输出状态 $h_t$ 是正向隐藏状态 $h_t^\rightarrow$ 与反向隐藏状态 $h_t^\leftarrow$ 的拼接结果：

$h_t^\rightarrow = f(U^\rightarrow h_{t-1} + W^\rightarrow x_t + b^\rightarrow) \tag{13}$

$h_t^\leftarrow = f(U^\leftarrow h_{t+1} + W^\leftarrow x_t + b^\leftarrow) \tag{14}$

$h_t = [h_t^\rightarrow, h_t^\leftarrow] \tag{15}$

其中， $U^\rightarrow$ 、 $W^\rightarrow$ 分别为正向传播中的权重矩阵与输入权重， $b^\rightarrow$ 为偏置项； $U^\leftarrow$ 、 $W^\leftarrow$ 与 $b^\leftarrow$ 为反向传播对应参数。

本研究采用双层BiGRU对CNN提取的局部特征进行深度建模与精细筛选，以提升预测性能。

2.3.3 注意力机制

注意力机制通过为编码器和解码器之间的交互分配最优权重，突出关键信息的作用，从而提高神经网络的整体效率。该机制通过有选择地聚焦于最相关的输入，不仅降低了计算复杂度，还增强了网络的表达能力。

如图5所示，注意力机制通过处理任务相关的查询向量（ $q$ ）来计算其与关键向量（ $k$ ）之间的分布关系，并将该分布应用于相应的数值向量（value），从而生成注意力值。这一计算过程展示了注意力机制如何简化神经网络模型的复杂度。相比处理全部 $N$ 个输入，通过集中关注部分关键输入，注意力机制有效降低了计算负担并提升了聚焦效率。
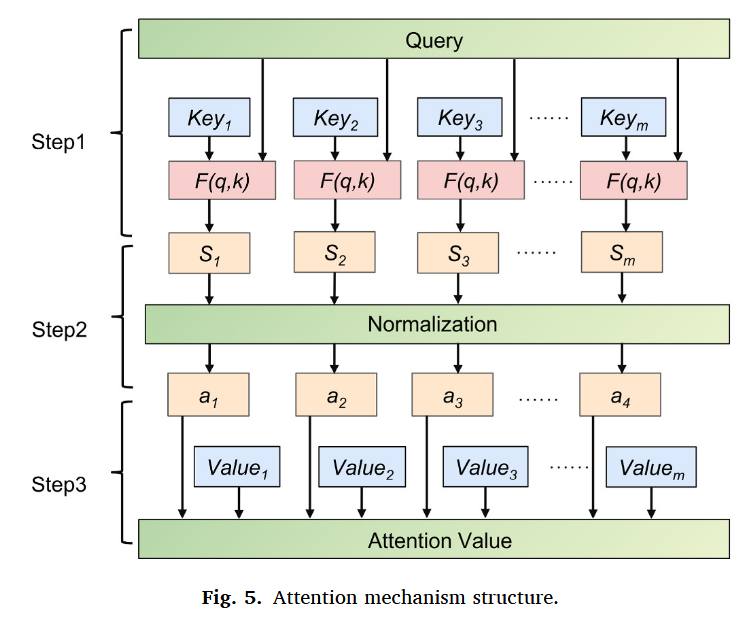
在这里插入图片描述

在本研究中，注意力机制与 BiGRU 模型结合，借助概率分布的方式提取关键时间序列特征之间的关联。具体地， $x_i$ （ $\in [1, n]$ ）表示 BiGRU 的输入， $h_i$ 表示对应的隐藏层输出， $\beta_i$ 表示注意力分布的权重， $y$ 表示带有注意力机制的 BiGRU 输出。

注意力权重的计算公式如下：

$g_t = s \cdot \tanh(w \cdot h_t + b) \tag{16}$

$\beta_i = \frac{\exp(g_t)}{\sum_{j=1}^{i} g_j} \tag{17}$

$d_i = \sum_{t=1}^{i} g_t \cdot h_t \tag{18}$

其中， $g_t$ 是由 BiGRU 输出 $h_t$ 计算得到的注意力得分， $s$ 、 $w$ 为可训练的权重参数， $b$ 为偏置项， $d_i$ 为注意力层在时间步 $t$ 的输出结果。

2.4 模型性能评估

为了量化 CNN-BiGRU-Attention 模型的预测精度，本文采用了多种常用评估指标，包括 RMSE、MAPE、MAE 和 $R^2$ 。这些指标定义如下：

$\text{RMSE} = \sqrt{ \frac{1}{N} \sum_{t=1}^{N} (y_t - \hat{y}_t)^2 } \tag{19}$

$\text{MAPE} = \frac{1}{N} \sum_{t=1}^{N} \left| \frac{y_t - \hat{y}_t}{y_t} \right| \tag{20}$

$\text{MAE} = \frac{1}{N} \sum_{t=1}^{N} |y_t - \hat{y}_t| \tag{21}$

$R^2 = 1 - \frac{ \frac{1}{N} \sum_{t=1}^{N} (y_t - \hat{y}_t)^2 }{ \frac{1}{N} \sum_{t=1}^{N} (y_t - \bar{y})^2 } \tag{22}$

其中， $N$ 表示样本总数， $y_t$ 和 $\hat{y}_t$ 分别表示实际值和预测值， $\bar{y}$ 表示实际值的均值。

在预测具有阶跃特征的滑坡位移时，样本中包括渐变阶段和突变阶段，但突变样本数量相对较少。尽管如此，准确预测突变阶段至关重要，因为它们代表了滑坡高风险的不稳定时期（Long 等，2022）。

为此，本文提出了一种非线性加权高损失函数（NLWHL），通过提高突变阶段误差的权重，以增强模型对异常变化的敏感性。非线性加权系数的计算公式如下：

$\text{weight}_t = \frac{1 + k \cdot e^{\alpha \cdot y_t}}{ \sum_{t=0}^{N} (1 + k \cdot e^{\alpha \cdot y_t}) } \tag{23}$

随后，NLWHL 损失函数结合了上述加权值，对每个观测点计算加权误差项：

$\text{NLWH}_t = \sum_{t=0}^{N} \text{weight}_t \cdot L(\varepsilon_t) \tag{24}$

$\varepsilon_t = y_t - \hat{y}_t \tag{25}$

$L(\varepsilon_t) = \begin{cases} 0.5 \cdot \varepsilon_t^2, & \text{若 } |\varepsilon_t| \leq \delta \\ \delta \cdot |\varepsilon_t| - 0.5 \cdot \delta^2, & \text{否则} \end{cases} \tag{26}$

其中， $k$ 、 $\alpha$ 和 $\delta$ 为可调节的超参数，分别控制突变样本的权重缩放程度和损失函数的鲁棒性。该损失函数不仅优化了整体预测误差，还特别加强了模型对突变阶段的适应能力。

3. 案例研究

3.1 白水河滑坡背景

本研究选取白水河滑坡作为案例分析对象。该滑坡活动持续不断，因其强烈的位移曾多次引发预警。如图6所示，白水河滑坡位于三峡库区秭归县长江右岸，距离三峡大坝下游56公里。其地形三面环山、一面临江，极易受到降雨影响。滑坡区域自北向南地势逐渐升高，前后高差约330米。水平方向上，滑坡东西跨度约700米，被一条南北走向的基岩山脊分隔，纵向跨度约770米。滑坡整体坡度在 $30^\circ$ 至 $35^\circ$ 之间，平均厚度约30米，总体积约为 $1260 \times 10^4 \ \text{m}^3$ 。
在这里插入图片描述

从地质角度来看，白水河滑坡处于中厚层砂岩基岩层中，层理倾角由 $36^\circ$ 逐渐减小至 $15^\circ$ （见图7）。该滑坡类型为堆积型土质滑坡（Zou 等, 2020b）。结构上，滑坡主体由松散的砾石土与粉质黏土组成，滑动带主要由含砾粉质黏土或碎石组成，其下伏基岩为中等风化程度的泥质粉砂岩，发育有明显节理裂隙。
在这里插入图片描述

地形上，滑坡呈阶梯状结构，上部陡峭，中部地形相对平缓，有利于侵蚀物质的积累（Deng 等, 2021）。历史上，白水河滑坡自古以来滑动活动频繁，属于典型的古滑坡体。2003年6月，当滑坡区域水位升至135米时，由于水位骤变及库区调节机制的周期性作用，导致原有滑坡复活，引发一系列新的滑坡。在此背景下，部署了一套完整的滑坡监测系统，系统布设详尽。

3.2 监测数据

为监测滑坡位移，在滑坡体内布设了多个GPS监测站。其中，位于滑坡核心区域的 ZG118 监测点被选为代表点，用于捕捉和记录滑坡全过程位移变化。ZG118 点的数据集具有代表性，适用于数据驱动模型的开发。因此，本文采用该监测点的数据评估所提方法的可行性与有效性。如图8所示，包含降雨量、水库水位以及ZG118点位移数据的监测曲线展现出白水河滑坡“阶跃式”变化的特征。
在这里插入图片描述

对位移数据的分析显示，自蓄水启动以来，滑坡年位移量逐年上升，尤其在每年5至7月的雨季，伴随着水位下降和水位减缓，位移显著加剧。通常在6月或7月出现“跳跃式”突变，主要由强降雨或水位快速下降触发，称为突变状态事件。而在其他水位上升或高水位时段，滑坡位移较为平稳，呈蠕滑状态。降雨与库水位的波动对滑坡位移的演化具有重要影响，是位移变化的主要触发因素。

4. 结果与分析

4.1. 位移分解与相关性分析

通过使用CEEMDAN算法对白水河滑坡的累积位移进行分解，得到了五个复杂度不同的IMF分量以及一个残差RE，如图9所示。图10表明，这五个IMF分量构成了滑坡位移的周期性部分，代表由外部因素引起的滑坡位移；而残差RE则代表滑坡位移的趋势部分，反映了由内部因素引起的位移。
在这里插入图片描述

趋势位移与监测周期呈现近似线性关系，而周期性位移则表现出明显的周期性。周期性部分与累积位移的阶梯状周期特征一致。因此可以得出结论，准确预测周期性位移对于提高累积位移预测精度具有重要影响。

表2提供了15个候选变量与周期性位移之间的详细相关性分析。值得注意的是，不同诱发因子类型的最大信息系数（MIC）表现存在显著差异，其中水库水位波动相较于历史降雨和水位数据呈现出更平滑的特征。
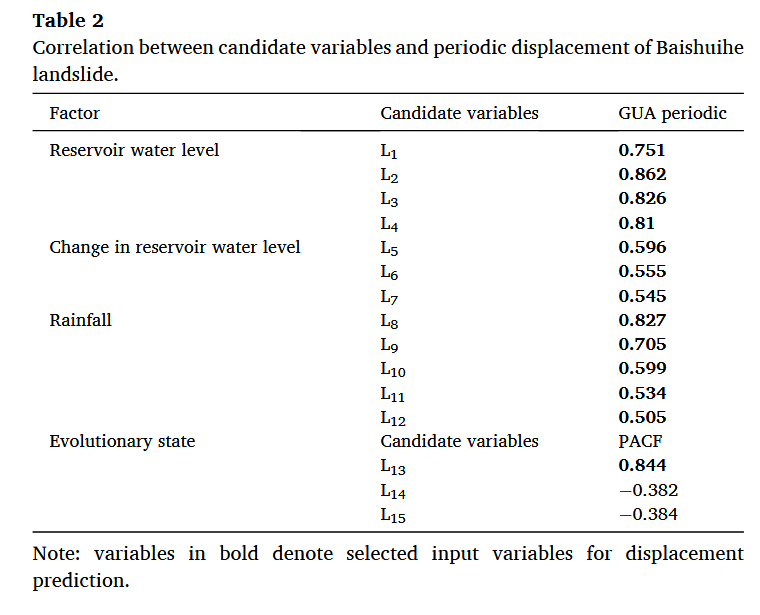
在这里插入图片描述

在这些候选变量中，白水河滑坡的周期性位移对前两个月的水库水位（L2）表现出高度敏感，MIC值为0.862；当月降雨量（L8）与周期性位移之间也存在较强相关性，MIC值为0.827。这表明滑坡的周期性位移主要受前期降雨和水库水位的影响，这些因素共同构成了滑坡位移演化的动态特征。

在演化状态因子方面，最优的滞后阶为L13，表明前一个月的周期性位移最能代表当前滑坡坡体的状态。因此，为了实现位移的精准预测，最终选取了13个最具代表性的候选变量作为输入，用于构建更为准确的位移预测模型。

4.2. 位移预测

4.2.1. 周期性位移预测

在周期性位移预测中，评估所提出模型的性能需与已有研究中的模型进行比较。这些模型包括：

单一动态模型：如GRU、LSTM
混合静态模型：如Slime Mold Optimization优化的支持向量机（SMA-SVM）
混合动态模型：如SMA-GRU、SMA-LSTM
混合深度学习模型：如BiGRU-Attention、CNN-BiLSTM 和 CNN-BiGRU

模型的超参数设置详见表3。图11和图12分别展示了训练集与测试集上九种模型的预测结果。图13中则量化展示了各模型的R²分数，结果表明，CNN-BiGRU-Attention模型在训练和测试阶段均取得最高R²分数（0.9870）。
在这里插入图片描述

尽管所有模型在趋势变化的预测上表现良好，但在突变峰值处仍存在较大误差。相比之下，CNN-BiGRU-Attention模型在局部峰值识别方面表现优异，显著提升了整体预测性能。

图14总结了各模型在训练和测试集上的关键性能指标，包括RMSE、MAPE、MAE、R²和运行时间：
在这里插入图片描述

在训练集上：
- GRU 和 LSTM 分别的 RMSE 为 62.29 和 62.80，MAE 为 35.1 和 39.18，MAPE 为 1.42 和 2.47，R² 为 70.36 和 65.08。
- 混合静态模型 SMA-SVM 性能提升明显，RMSE 为 47.86，MAE 为 21.66，MAPE 为 1.31，R² 为 76.83。
- SMA-GRU 和 SMA-LSTM 表现更优，RMSE 为 44.47 和 46.63，MAE 为 26.53 和 27.37，MAPE 分别为 1.72 和 1.76，R² 为 0.80 和 0.77。
- 引入注意力机制的 BiGRU-Attention 模型进一步优化，RMSE 为 29.85，MAPE 为 1.43，R² 为 0.91。
- CNN-BiGRU 和 CNN-BiLSTM 模型显著增强性能，RMSE 分别为 13.36 和 13.52，MAE 为 8.90 和 9.81，MAPE 为 0.65 和 0.49，R² 均为 0.98。
- CNN-BiGRU-Attention 模型最优，RMSE 为 9.8，MAE 为 6.78，MAPE 为 0.78，R² 达 99.97。

该模型的优越性来源于 CNN 的特征提取能力、BiGRU 的序列建模能力以及注意力机制的重点学习能力，三者有效结合，极大提升了时空信息的捕捉能力与预测精度。

在测试集上：
- GRU 和 LSTM 模型在周期位移曲线特征的刻画方面表现较差，RMSE 为 46.89 和 29.79，MAE 为 36.61 和 23.22，MAPE 为 3.95 和 3.47，R² 分别为 41.98 和 77.46。
- SMA-GRU、SMA-LSTM 和 SMA-SVM 模型在局部峰值处预测值波动较大，RMSE 分别为 15.85、16.19 和 19.47，R² 分别为 94.9、78.88 和 77.85。
- BiGRU-Attention、CNN-BiGRU 和 CNN-BiLSTM 表现明显更优，RMSE 分别为 10.84、11.09 和 15.23，R² 为 0.93、0.93 和 0.88。
- CNN-BiGRU-Attention 模型在测试集中表现最为出色，RMSE 为 8.11，MAE 为 6.62，MAPE 为 0.86，R² 高达 98.66，充分展示了其在滑坡周期位移建模中的优势。

图15展示了九种不同模型的运行时间。GRU 和 LSTM 模型的运行时间分别为 13.95 秒 和 10.85 秒。引入 SMA 算法的模型（即 SMA-GRU、SMA-LSTM 和 SMA-SVM）运行时间分别上升至 25.93 秒、25.5 秒 和 15.36 秒。值得注意的是，SMA-SVM 的运行时间增加相对较小，这归因于其结构较为简单的 SVM 模型。
在这里插入图片描述

相比之下，引入注意力机制的模型（如 BiGRU-Attention）运行时间为 22.52 秒，低于 SMA-GRU 和 SMA-LSTM。而 CNN-BiGRU-Attention 模型进一步将运行时间缩短至 13.98 秒，这体现了 CNN 模块在高维特征提取方面的快速性。CNN-BiGRU 和 CNN-BiLSTM 模型运行时间最短，分别为 8.17 秒 和 6.39 秒，进一步证明 CNN 模块在高维特征提取方面的效率优势。

CNN-BiGRU-Attention 模型之所以在准确性上表现优异，主要得益于其对空间和时间信息的综合利用：CNN 高效提取输入序列中的空间特征，BiGRU 捕捉序列中的时间相关性，同时注意力机制聚焦于关键信息。这种空间与时间特征的协同建模极大提升了模型性能。

此外，该模型引入的重置门和更新门机制使其能够充分利用历史信息，并自适应地响应新输入数据，从而进一步增强预测准确性。通过不断学习数据之间的关联变化，模型能够自动适应不断演化的数据环境，减少无效规则对预测结果的影响，最终显著提升预测性能。

这一学习机制使得模型能够对滑坡位移的动态过程做出更合理的刻画，从而有效提升了预测精度。

4.2.2 趋势位移预测

趋势位移主要受内部地质因素的影响，呈现出逐渐演化的特征，往往依赖经验知识进行建模，而不依赖于降雨或水库水位等外部变量。遗憾的是，许多先前的研究忽视了对趋势项位移的预测。然而，准确预测趋势项位移对于提升滑坡累计位移预测的精度具有重要意义。

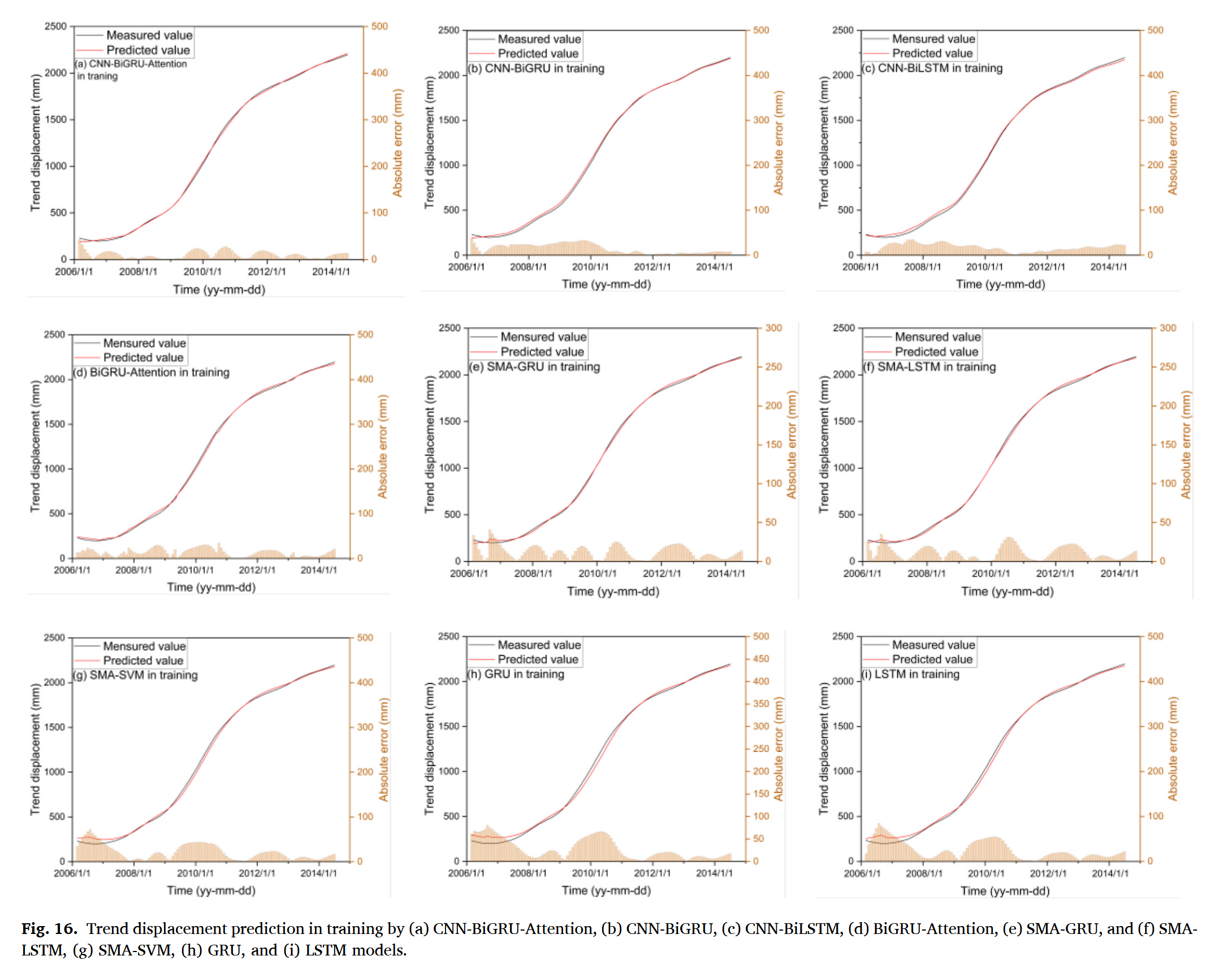
图16和图17展示了趋势位移预测结果与实际位移的整体一致性。图18中的 R² 分数进一步验证了这些模型的有效性。训练集与测试集的 RMSE、MAPE、MAE、R² 和运行时间几乎一致，说明各模型在趋势项预测方面均表现出良好的泛化能力和预测性能。
在这里插入图片描述

4.2.3 累计位移预测

根据公式 (1)，通过对趋势位移与周期位移的线性组合，计算出各模型的累计位移预测值，结果如图19和图20所示。九种不同模型在位移预测趋势上表现相似。然而，在发生突变的状态下，各模型预测值的分布存在差异。这种差异反映出各算法在预测中的不确定性不同，不能保证每次预测都具有绝对准确性。
在这里插入图片描述

在所有模型中，CNN-BiGRU-Attention 模型的 R² 值最高，达 0.994（见图21）。在训练集（图19）中，CNN-BiGRU-Attention 模型展现出对白水河滑坡整体位移特征的卓越拟合能力。值得注意的是，最大绝对误差出现在2009年11月，这可能是由于该时期周期位移预测存在一定偏差，进一步说明周期位移对累计位移预测精度具有直接影响，特别是对于具有阶梯状曲线特征的滑坡位移数据。
在这里插入图片描述

四个评估指标的结果总结在图22和表4中。从整体效果看，融合 CNN 的混合模型（CNN-BiGRU 和 CNN-BiLSTM）仅次于 CNN-BiGRU-Attention 模型；其次是融合注意力机制的 BiGRU-Attention 模型。混合动态模型（SMA-GRU 和 SMA-LSTM）在 RMSE、MAPE、MAE 和 R² 上表现几乎相同，整体优于静态混合模型 SMA-SVM，这主要得益于混合动态模型在考虑周期项时的更高准确性。
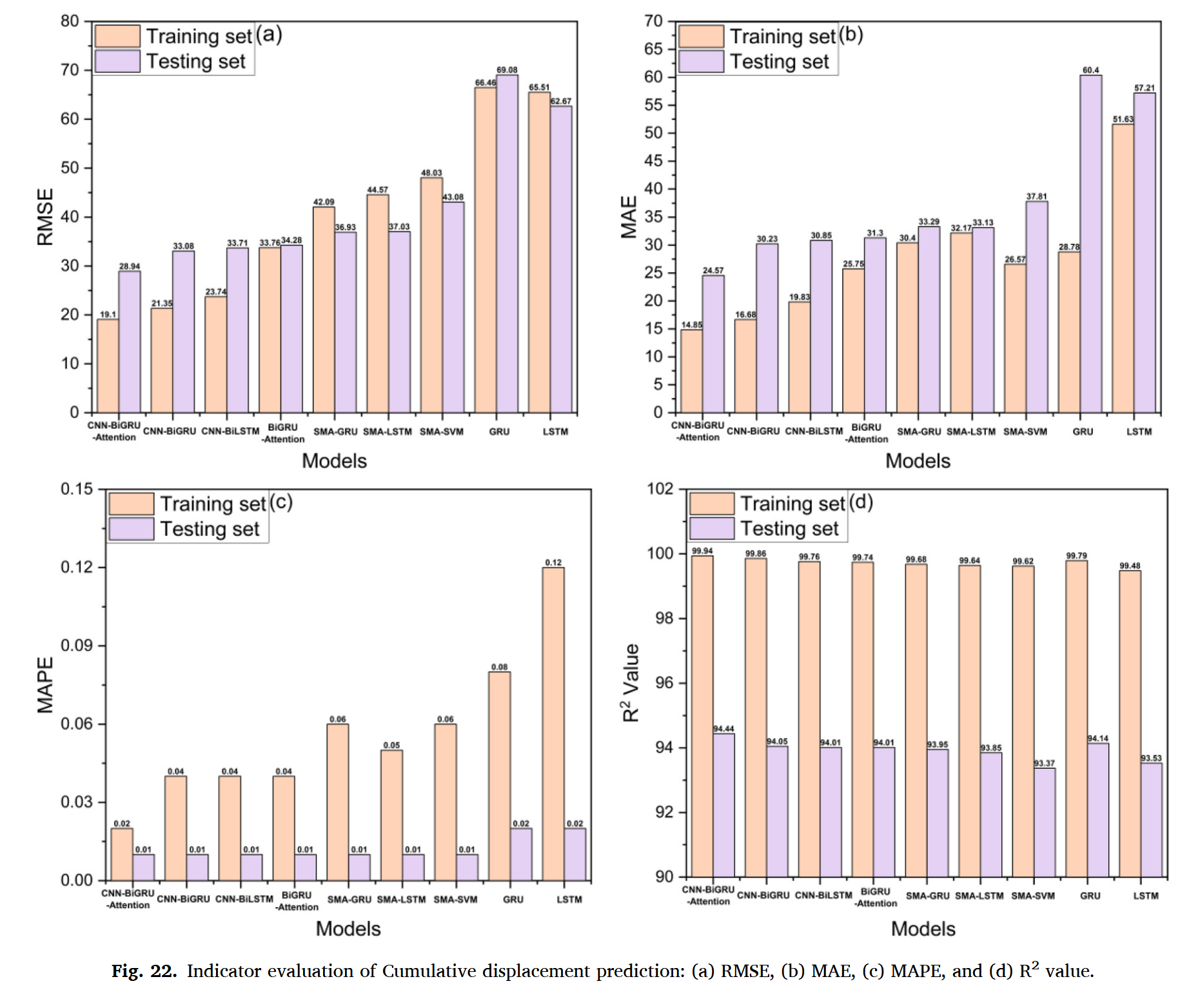
在这里插入图片描述

相比之下，静态混合模型 SMA-SVM 又明显优于单一的 GRU 和 LSTM 模型，体现在更低的 RMSE、MAPE、MAE 和更高的 R² 值。在测试集（图22）中，CNN-BiGRU-Attention 模型的 RMSE、MAPE 和 MAE 值最低，R² 值最高，说明其在预测白水河滑坡位移方面具有更高的准确性。

从 RMSE、MAPE、MAE 和 R² 各指标来看，CNN-BiGRU、CNN-BiLSTM 和 BiGRU-Attention 模型预测精度相近，仅次于 CNN-BiGRU-Attention。两个混合动态模型（SMA-GRU 和 SMA-LSTM）的预测精度也非常接近，并且明显优于 SMA-SVM、GRU 和 LSTM。GRU 和 LSTM 表现较差的原因可能在于参数调整工作量大，容易在训练集上过拟合，导致泛化能力不足。

相比之下，CNN-BiGRU-Attention 模型表现出更强的泛化能力，从而显著提升了预测精度。

综合考虑 RMSE、MAPE、MAE 和 R² 各项指标的最优值，五种主要算法的预测性能排序如下：

CNN-BiGRU-Attention > CNN-BiGRU > CNN-BiLSTM > BiGRU-Attention > SMA-GRU > SMA-LSTM > SMA-SVM > LSTM > GRU

4.2.4. 非线性加权 Huber 损失函数（NLWHL）误差评估

在位移突变阶段，滑坡对外部影响因素的敏感性显著增强。因此，外部因素的突发性变化可能导致滑坡位移的剧烈变动，甚至诱发滑坡灾害。为了更加准确地评估各模型在突变位移预测中的表现，本文引入了非线性加权Huber损失函数（NLWHL），该函数能够突出在滑坡突变状态下的预测误差。

图23展示了基于NLWHL评估的各模型在白水河滑坡预测中的误差表现。其中，CNN-BiGRU-Attention模型表现最为优越，超过90%的预测误差低于0.008（见图23(a)）。各模型的详细预测误差值列于表5，其中 CNN-BiGRU-Attention 模型在蠕滑状态（creeping state）下的误差最低，仅为 0.177。一般来说，在蠕滑状态下出现一定误差是可以接受的。
在这里插入图片描述

为优先提高对因水库调节而引发的、具备渐进演化特征的滑坡突变状态的预测精度，我们采用 NLWHL 对各模型的预测误差进行计算与评估。图23(b) 显示，CNN-BiGRU-Attention 模型在突变状态（abrupt state）下的平均误差最小，仅为 1.299。

能够准确预测位移突变状态对于滑坡的预警和干预具有关键意义，有助于尽早识别潜在危险状态，显著降低滑坡事件可能带来的风险与损失。

综上所述，从所有角度综合考量，CNN-BiGRU-Attention 模型在本研究所涉及的所有模型中展现出最小的预测误差，在蠕滑状态和突变状态下均具有优异表现。

5. 讨论

5.1. 方法的优势

本研究展示了 CNN-BiGRU-Attention 模型在滑坡位移预测中的显著表现，优于 GRU、LSTM、SMA-SVM、SMA-GRU、SMA-LSTM、BiGRU-Attention、CNN-BiGRU 和 CNN-BiLSTM，原因如下：

与传统模型如 GRU 和 LSTM（侧重时间序列数据但通常忽略空间特征）以及 SMA-SVM（强调特定数据处理而非空间特征）不同，CNN-BiGRU-Attention 模型集成了 CNN 用于空间特征提取，BiGRU 用于强大的时间相关性建模。
相比于 CNN-BiGRU 和 CNN-BiLSTM，将注意力机制集成到 CNN-BiGRU 模型中使得模型能够精确预测与周期组件相关的滑坡位移。该模型有效解决了滞后效应，并通过 BiGRU 捕捉了长期依赖关系。
CNN-BiGRU-Attention 模型的重置门和更新门设计使其能够适应新的输入数据，处理变化的数据模式，确保了模型的多样性。

总而言之，时间和空间特征的融合、注意力机制的引入以及灵活的模型设计使得 CNN-BiGRU-Attention 模型在涉及阶梯状曲线的滑坡位移预测任务中表现卓越。而其他模型则可能面临这些因素的局限性，从而导致预测精度下降。

5.2. 限制与未来研究

本文提出的模型适用于预测具有阶梯状曲线特征的滑坡位移，并且也适用于预测趋势项。然而，仍然有进一步改进的空间。在建模方面，复杂的深度学习结构和注意力机制使得模型可能缺乏可解释性，难以理解模型在特定预测中的决策过程。未来的研究应当开发可解释的深度学习模型。在数据方面，降水量的突然变化、水位变化或不可预见的气象事件可能导致位移预测误差的增加。此外，考虑到本研究使用的是一个月的数据点，这在一定程度上限制了其有效的滑坡位移预警能力。因此，未来的研究应探索涵盖更广泛影响因素（如地质条件和构造应力）的滑坡预测方法。此外，后续研究应整合滑坡破坏机制，构建双驱动的物理和数据模型，以应对滑坡预警中的挑战。

6. 结论

本研究提出了一种优化的 CNN-BiGRU 模型，并引入注意力机制，用于预测具有阶梯状曲线特征的滑坡位移。该模型基于 CEEMDAN 算法对滑坡位移进行分解，利用 CNN 模型从多源数据中提取复杂的高维动态特征，注意力机制则增强了模型对关键信息的关注能力，能够有效提取降雨、水位与历史位移之间的关系。最终，采用非线性加权 Huber 损失函数（NLWHL）对各模型在渐变与突变状态下的预测性能进行了评估。主要研究结论如下：

(1) CNN 层能够有效提取复杂的高维动态特征，BiGRU 模块则擅长捕捉历史数据中的时间相关性，而注意力机制则使模型能够聚焦于降雨、水位和历史位移数据中的关键信息。在周期项预测中，CNN-BiGRU-Attention 模型表现出优越性能，测试集中 RMSE 相较于 CNN-BiGRU、CNN-BiLSTM、BiGRU-Attention、SMA-GRU、SMA-LSTM、SMA-SVM、GRU 和 LSTM 分别降低了 25.18%、26.87%、46.75%、56.88%、57.14%、64.82%、82.70%、72.78%，显示出该模型在周期项预测中的高精度优势。

(2) 在趋势项位移预测方面，各模型的预测性能相近，说明总体滑坡位移预测的精度主要受周期项预测准确性的影响。在累计位移预测中，CNN-BiGRU-Attention 模型依旧表现最优，其测试集 RMSE 分别比 CNN-BiGRU、CNN-BiLSTM、BiGRU-Attention、SMA-GRU、SMA-LSTM、SMA-SVM、GRU 和 LSTM 低 12.52%、14.15%、15.58%、21.68%、21.84%、32.81%、58.10%、53.81%，充分体现出该模型在总体滑坡位移预测中的高准确率。

(3) NLWHL 的引入强调了滑坡阶梯状突变状态下的预测精度。CNN-BiGRU-Attention 模型在蠕变状态和突变状态下的误差分别为 0.177 和 1.299，均为所有模型中最低。对突变状态位移的评估为滑坡早期识别与干预提供了必要契机。

展望未来，本研究为进一步探索提供了多个有意义的方向。首先，将该模型推广应用于其他水库滑坡位移预测中，有望进一步增强模型的适应性与鲁棒性。其次，本文未涉及地质构造、构造应力等物理因素，未来研究应致力于引入滑坡破坏机制，构建融合物理驱动与数据驱动的双驱动模型，以更全面地应对滑坡预警中的复杂挑战。最后，值得注意的是，该模型的适应性也可拓展至交通流预测等其他领域，其通用性和可扩展性值得进一步探索。