李宏毅机器学习系列-分类-概率生成模型

分类及其应用

分类简单来说就是你输入一个x，经过一个函数，给你输出一个值n，即属于哪个类，n是个离散的数值：

主要应用有：
信用评分：比如你去贷款，他会根据你的收入，存款，职业，年龄等因素来评估是否要贷款给你。
医疗诊断：根据当前的症状，年龄，以往病史，来推断可能属于类疾病。
手写识别：给一张图，判断是哪个类，每一个字可能就对应一类。
人脸识别：给定一张图，判断是不是人脸。

宝可梦分类案例

举个宝可梦分类的案例比较接地气，我们有很多宝可梦，每个宝可梦都属于一个类别，比如皮卡丘是雷电系，杰尼龟是水系，妙蛙草是草系，我们要做的就是找出一个模型，输入是宝可梦的信息，输出是属于哪个系：

我们有一堆宝可梦的信息，比如血量，攻击力，防御力，特殊攻击力，特殊防御力，速度等，我们要根据这些来判断他是哪个系的：

那为什么要做系的判断呢，有什么意义呢，因为不同的系之间有克制关系，如果我们能靠这些来预测一个不知道系的宝可梦，那对战的时候可以用克制他系的宝可梦对付他，当然是很有用的啦，请看克制关系图，左边是攻击方，上边是防御方，不同系之间是有伤害倍数克制关系的：

那我们想要解决这么一个分类问题，就可以用机器学习的方法，那二分类来说，我们有个模型$f(x)$，输入是x，输出是类别1或者类别2，当然模型里面可以判断x是否大于0，是就分为类别1，不是就类别2，然后我们定义损失函数，如果预测的和真实的不一样，损失函数就越大，反之就越小，最后我们找出最好的那个模型，可以用感知机，也可以用支持向量机(SVM)，当然我们这里先不用这些：

用回归来做分类

那我们要怎么做分类呢，我们首先定义数据对(输入，类别)：

如果我们用学过的回归的方法来做分类会怎么样呢，比如拿二分类来说，我们定义类别1的目标值为1，类别二的目标值为-1，当然真实情况不可能真的是1和-1，只是说接近1的就是类别1，接近-1的是类别2：

我们的模型定义为$y=b+w_1{x}_1+w_2{x}_2$,对于样本比较集中的情况就是这样，分界线绿色线条就是$b+w_1{x}_1+w_2{x}_2=0$：

但是如果某些样本离的比较远的话，会被认为误差很大，为了减少误差，分界线就进行旋转，即为紫色线条，以减少整体误差，但是这样反而不能很好的将其分类，可以看到：

也就是说，回归问题对误差是比较严格的，可能跟定义的损失函数有关系，一般是均方差，严格要求误差小，而分类问题一般有个阈值，能区别出来就行，对误差没那么严格的要求。

还有个问题就是，如果用回归来做多分类的话，会使得很多类别都很接近，很相似，貌似让他们之间有某种关系，但是其实他们是没关系的，这样可能对分类任务不是很好。那要怎么办呢，我们再来看看经典的概率问题。

概率模型

假我们有两个盒子，蓝色的为B1，绿色的为B2，分别放入不同数量的蓝球和绿球，现在要问，从其中抽出一个篮球是来自B1的概率是多少。

这个问题应该算是贝叶斯概率问题，执果索因。我们假设从B1抽取的概率是2/3,从B2抽取的概率是1/3,那我们就可以得到条件概率，即B1里抽取蓝色的概率为4/5,绿色的为1/5,B2抽取蓝色为2/5,绿色的为3/5。

那所求的就是：

其实是贝叶斯公式，直观理解就是我抽到了篮球，这个球是来自B1的概率，也就是我选择B1的概率$P(B_1)$，又在B1里抽了个篮球的概率$P(Blue|B_1)$，除以我抽到篮球的情况的总共的概率和(从B1里抽到篮球和从B2里抽到篮球的概率和$P(Blue|B_1)P(B_1)+P(Blue|B_2)P(B_2)$).

如果把他当成二分类来看就是：

我们可以求得给定任意的x，是来自分类C1的概率：

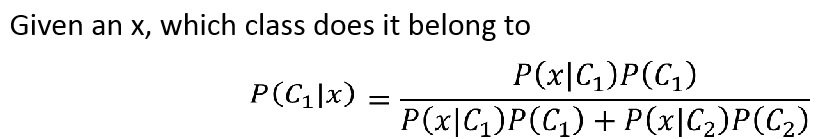
于是我们可以有个生成模型：

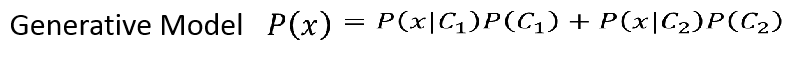
也就是说某个样本出现的概率可以是所有类别产生的概率的和，如果我们知道所有的样本出现的概率，我们就知道了这个样本的分布，那我们就可以用这个分布进行采样，产生样本，这个就叫做生成模型。、

先验概率

我们先来看看$P(C_1),P(C_2)$，这两个属于先验概率，我们拿ID<400的宝可梦做训练集，取出里面79只水系和51只一般系，因为这两个种类比较多，所以拿这两种做二分类例子。然后我们就可以算出$P(C_1),P(C_2)$的概率啦，就是类别数量除以总共的数量：

那怎么求从某个类别采样出样本的几率呢，比如$P(x|C_1)$，样本从$C_1$这个类别采样出来的概率。举个例子比如想求一只海龟从水系采样出来的概率：

然而我们的训练集里的水系有79只，并没有这只呀，难道概率是0，当然不是啦，这海龟一看脸就是水系的，我们的79只只是一部分而已啦，那要怎么求这个呢，首先我们会把每一个宝可梦描述成一个向量，向量的维度就是他们的各种特征，这个也叫做特征向量：

然后我们把他们画出来，虽然他们属性有7个，但是7维的不知道怎么可视化，所以只考虑两个维度，防御力和特殊防御力，每个宝可梦都描述为二维向量，蓝色点就是水系分布：

那我们的海龟也可以在里面，我们假设这79只水系的是从某个高斯分布中采样出来的，那海龟也应该是属于这个分布，因此只要知道分布是可以求出$P(x|Water)$的，比如红色的圈分布：

多元高斯模型

那我们现在要做的事就是基于这79个样本，找出这个高斯模型，那我们先来看看高斯模型吧，这个是概率密度函数，是跟概率成正比的，暂时可以理解为是概率，因为是二维的，所以原本是方差变成了协方差矩阵：

不同的$\mu ，\sum$会产生不同的分布，我们可以好像发现$\mu$表示分布的偏移，也就是几率分布最高点不一样：

而$\sum$表示分布的形状，应该说是分散程度：

那我们能不能用79个样本去估计$\mu ，\sum$呢，如果能估计出来如下图，那我们就分布就能确定了，也就是红色的圈，也就能找到海龟从这个分布里采样出来的几率，黑色的New x就是海龟，虽然离的原，但是也是有概率，只是非常小，当然如果在中心，也就是$x=\mu$那就是最大的：

极大似然估计

那我们怎么去估计$\mu ，\sum$呢，就要用到极大似然估计啦。因为能采样出这79个样本的分布有很多，比如下图的两个红圈，不同的$\mu ，\sum$就有不同的分布，很显然，右上角的分布采样出那79个点的几率比较低，左下角的比较高：

那什么样的分布是最好的呢，应该是这79个样本从分布里采用的概率最大，因为79个样本相互独立，所以这个概率就可以变成一个乘积的形式：

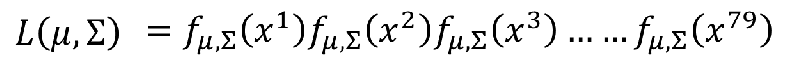
我们假设这79个样本是来自参数为$({\mu }^{\ast }，{\sum }^{\ast })$的高斯分布的可能性最大，因此我们要解决的问题就是：

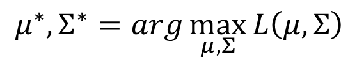
这个求法就不多说了，取对数，然后求导=0，可以算出这两个的估计值：

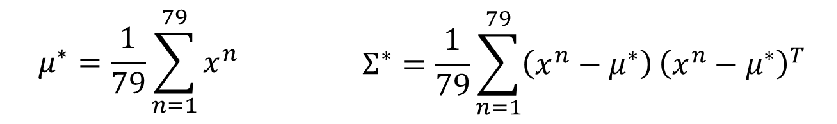
然后真正的结果如下，两个类别的参数：

前面我们要求的就是这个公式C1就是水系，C2就是一般系：


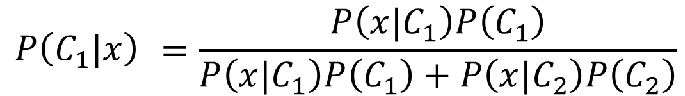
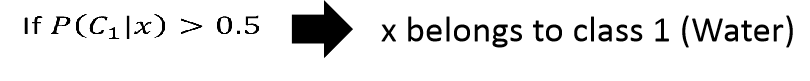
那我们现在知道了，$P(C1)=79/(79+61)=0.56,P(C2)=61/(79+61)=0.44$
而$P(x|C_1)$就是从$({\mu }^1，{\sum }^1)$里采样出来的几率，$P(x|C_2)$也同理，分别代入下列高斯公式即可：


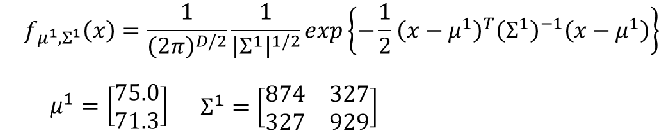
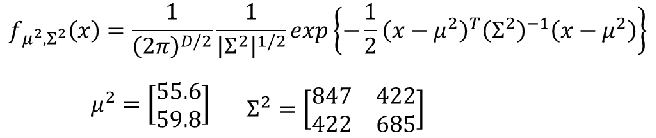
也就是这样：

然后我们看看结果，这个是训练集的分布图，蓝色点是水系，红色点是一般系，然后计算每一个点事C1水系的几率，可以看到红色的区域表示几率大的，蓝色区域表示小的：

然后我们进行分类，可以看到蓝色的在边界线外面，红色的在里面，但是貌似也不是分的很开：

再来看看测试集上的结果，好像也差不多：

测试集上的准确率是47%，好像不怎么样，没关系，这个只是二维，我们数据有7维，机器学习厉害的地方就是可以处理高维，高维中容易分，我们用了6维的数据，求得相应的高斯分布参数：

最后结果稍微好了点，但是不够啊：

改进

那要怎么办呢，通常来说，给每一个类别去共享一个协方差矩阵，因为协方差的尺寸是跟特征数量相关的，如果特征数量很大，协方差的尺寸也大，而且和特征数的平方成正比，这样不同的高斯分布有不同的协方差矩阵，这样模型的参数就会很多，就会过拟合，所以会不准，因此我们共享协方差，这样参数也少了：

那我们的极大似然估计的公式也要变啦，现在的参数就是两个均值，一个协方差矩阵：

他们有相同的协方差矩阵，就按概率加权平均来算：

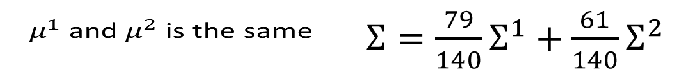
之后的结果边界变成一条直线了，这样的模型也叫做线性模型，考虑到所有的特征的时候准确率也提高了，在高维空间里貌似更容易线性可分：

总结下我们怎么解决这个分类问题，首先我们找一堆高斯模型作为模型集，然后用极大似然估计来定义模型的好坏，即可选出最好的模型：

为什么要先高斯模型呢，这个其实也不一定啦，看具体要求，简单的模型偏差大，方差小，复杂的模型偏差小，方差大。如果是二分类，其实可以用伯努利分布。如果假设我们的特征之间都是独立的，每一个概率都是一维的高斯分布，我们可以把问题化为：

这种假设就是朴素贝叶斯的思想。

后验概率

我们如果我们今天问某个样本是C1类的概率是多少，即：

上下同除以分子得：

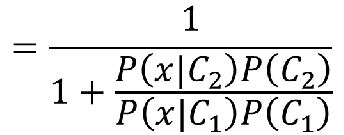
如果我们令：

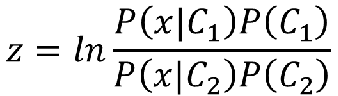
则得到：

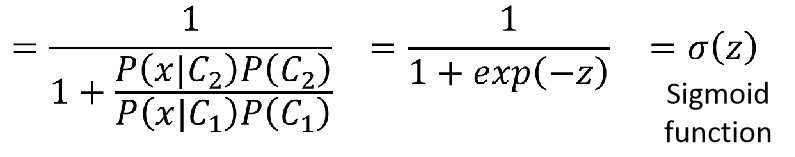
就是我们熟知的sigmoid激活函数：

然后我们来看下z到底是什么，首先把相乘换做相加，然后代入先验概率表达式：

然后对应的两个高斯概率密度函数为：

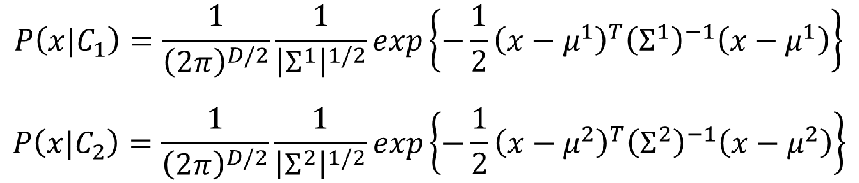
代入z中：

一堆公式推导，有关于矩阵的逆和转置的，了解下结论就行：

最后可以推导出我们很熟悉的式子，我们为什么那么麻烦的去把这个概率公式推出来，不直接用w和b呢，那就是下一篇要讲的逻辑回归啦。

总结

本篇主要介绍了分类问题，为什么不适合用回归来做，介绍了极大似然估计，介绍了多远高斯模型，还推导了sigmoid怎么定义的等等。附上思维导图：

好了，今天就到这里了，希望对学习理解有帮助，大神看见勿喷，仅为自己的学习理解，能力有限，请多包涵，图片来自李宏毅课件或者网络，侵删。