公式推导概率生成模型（更新～）

概率生成模型

  我们以二分类为例，说明基于概率的分类模型。理性情况下，我们大体可以将当前模型分成如下几步考虑：

1. Function(Model) :
   input : x -> f(x) -> output : class i
   其中，f(x) :
   当g(x) > 0 , output : class 1
   else , output : class 2
2. Loss :
   在训练集中获取正确分类结果的次数，即$L(f)={\sum }_n\delta (f(x^n)\ne {\hat{y}}^n)$
3. 找到最佳模型：比如：感知机、SVM。

  举例，比如我取某数据集的前140条数据作为training data，剩余数据作为test data。现在，

Training : 79条数据属于class 1，61条数据属于class 2。
则： $P(C_1)=79/(79+61)=0.56,P(C_2)=61/(79+61)=0.44$

贝叶斯公式与正态分布

  现在，我们给出一条数据x，那么它属于哪一类？这是一个很有意思的问题，如果大家学过概率论，那么就很容易联想到一个重要公式——贝叶斯公式。所以，根据贝叶斯公式，我们可以列出如下等式。假设我们现在求x属于class 1的概率：
$$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}$$
其中，根据全概率公式，$P(x)=P(x|C_1)P(C_1)+P(x|C_2)P(C_2)$，即产生$x$的概率分布，意味着我们可以“自己产生$x$”。这便是概率生成模型。
  如果这条数据x来自与我们划分好的训练集，那么很容易找到x在class 1和class 2的数目，即易计算出$P(x|C_1)$和$P(x|C_2)$。如果x并未出现在训练集中呢？显然，我们不能想当然的得出0的结果。道理很简单，这是很小的一部分数据集，并不代表全世界！所以如何处理呢？
  假设训练集中属于class 1的79条数据遵循一个整体的高斯分布（正态分布），当我们输入样本x的向量，输出x从该高斯分布里被取样出来的概率，即$P(x|C_1)$。那么这个高斯分布由什么参数决定呢？答案显然是均值$\mu$和方差$\Sigma$，他们的类型分别为向量和矩阵。公式如下：
f μ , Σ ( x ) = 1 ( 2 π ) D 2 1 ∣ Σ ∣ 1 2 e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } f_{\mu,\Sigma}(x) = \frac{1}{(2\pi)^{\frac{D}{2}}} \frac{1}{|\Sigma|^\frac{1}{2}}exp\{ -\frac{1}{2}(x-\mu)^T \Sigma^{-1} (x-\mu) \} fμ,Σ​(x)=(2π)2D​1​∣Σ∣21​1​exp{−21​(x−μ)TΣ−1(x−μ)}
  接下来，我们该如何寻找这两个参数？

极大似然估计

  如下图所示，任何一个高斯分布均可对这些点取样，只是取出的可能性不同。应用到上文的例子，相当于具有$\mu$和$\Sigma$的高斯分布的可能性等于该高斯分布取出这class 1的79个点的机率。

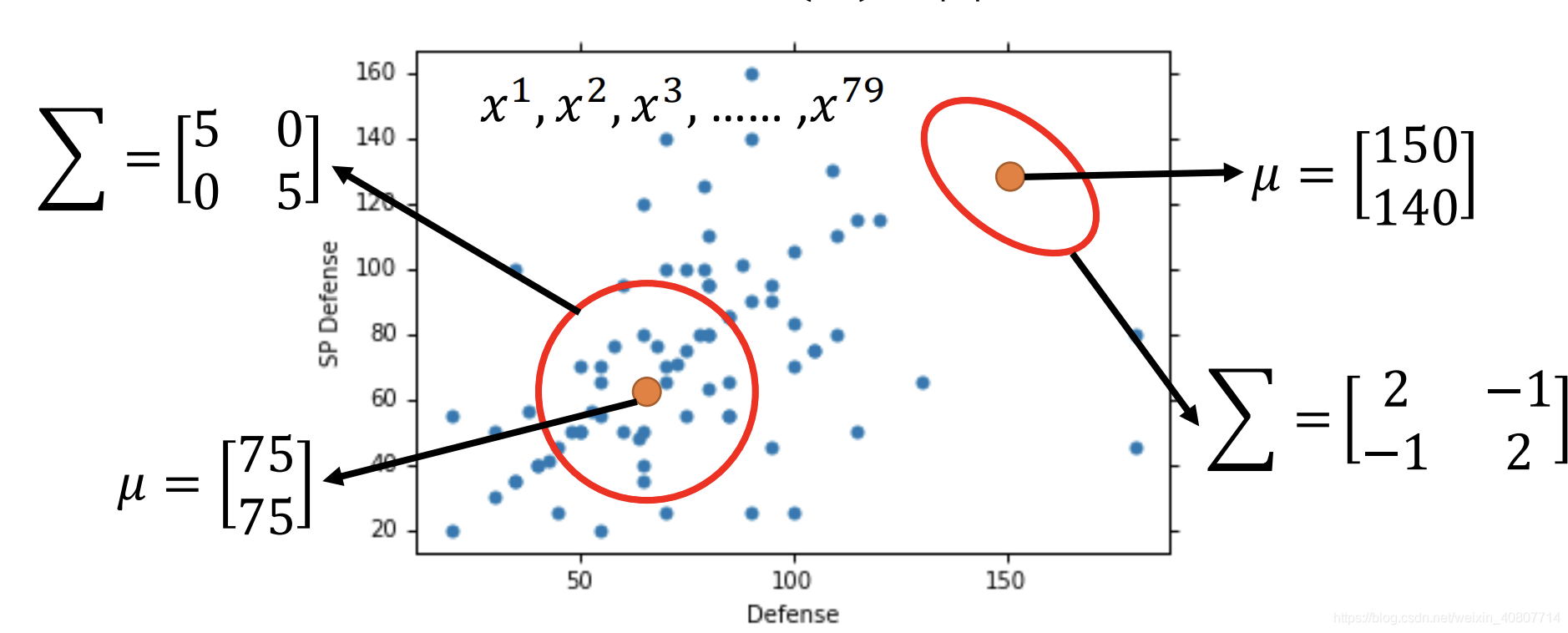
  假设$x^1,x^2,...,x^{79}$由同一高斯分布$({\mu }^{\ast },{\Sigma }^{\ast })$生成，我们通过极大似然估计找到取出这79个点机率最大的分布。即：
$$\begin{gathered} L(\mu ,\Sigma )=f_{\mu ,\Sigma }(x^1)\cdot f_{\mu ,\Sigma }(x^2)\cdot ...\cdot f_{\mu ,\Sigma }(x^{79}) \\ {\mu }^{\ast },{\Sigma }^{\ast }=arg\underset{\mu ,\Sigma }{\max }L(\mu ,\Sigma ) \end{gathered}$$
取对求导即可得出：
$$\begin{gathered} {\mu }^{\ast }=\frac{1}{79}\sum _{n=1}^{79}{x}^n \\ {\Sigma }^{\ast }=\frac{1}{79}\sum _{n=1}^{79}(x^n-{\mu }^{\ast })(x^n-{\mu }^{\ast }{)}^T \end{gathered}$$
这样就得出了关于class 1的$P(x|C_1)$。显然，我们同样可以求出参数不同的关于class 2的$P(x|C_2)$。万事俱备，我们终于可以做分类了！

分类

  现在回到开始，输入x属于class 1的概率：

• $$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}$$
  其中，$P(C_1)=0.56,P(C_2)=0.44,P(x|C_1)=f_{{\mu }^1,{\Sigma }^1}(x),P(x|C_2)=f_{{\mu }^2,{\Sigma }^2}(x)$.
• 如果$P(C_1|x)>0.5$，则x属于class 1。

如图所示，我们发现在训练集和测试集上的表现均不理想。即使推广到高维空间（7个特征），准确率依旧堪忧。为什么？

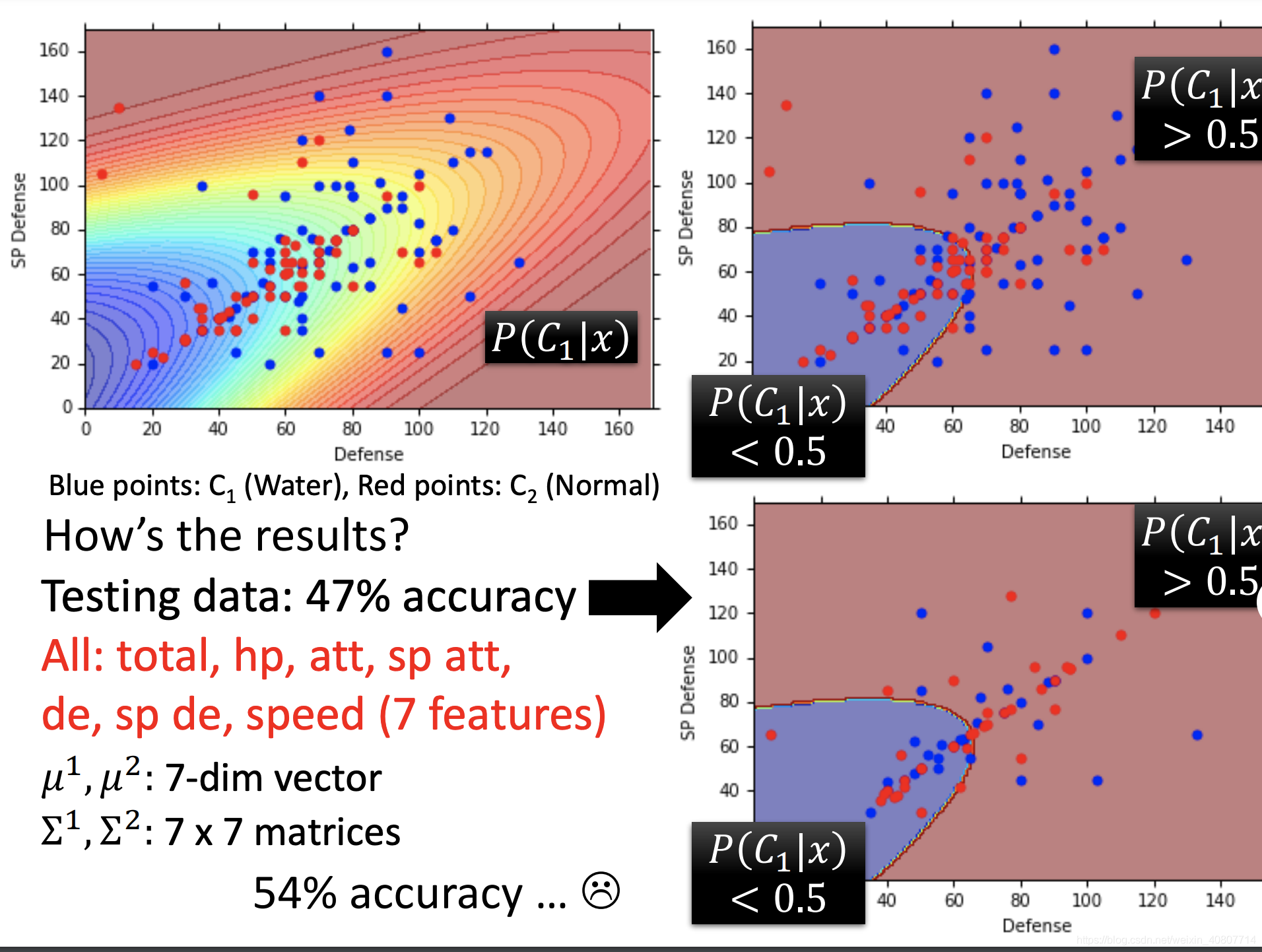
改进模型

  我们刚才给两个class分别赋予了$\mu$和$\Sigma$，然而在实际应用中，我们很少给每一个高斯分布分配自己的$\mu$和$\Sigma$。现在改进模型，让两个不同的class共享同一个协方差矩阵$\Sigma$。比如下图：

改进模型的极大似然估计

  现在做一下微小的变更，寻找${\mu }^1,{\mu }^2,\Sigma$，使其最大化似然函数$L({\mu }^1,{\mu }^2,\Sigma )$:
$$L({\mu }^1,{\mu }^2,\Sigma )=f_{{\mu }^1,\Sigma }(x^1)\cdot f_{{\mu }^1,\Sigma }(x^2)\cdot ...\cdot f_{{\mu }^1,\Sigma }(x^{79})\cdot f_{{\mu }^2,\Sigma }(x^{80})\cdot ...\cdot f_{{\mu }^2,\Sigma }(x^{140})$$
其中，${\mu }^1,{\mu }^2$依旧是样本均值，而$\Sigma =\frac{79}{140}{\Sigma }^1+\frac{61}{140}{\Sigma }^2$.
  结果如图，当我们推广到高维空间中，准确率有了显著提升。尽管高斯分布非线性，不过这个分界线是线性的，所以也可以说这是一个线性模型（linear model）。如果仍不理解，在最后的公式推导中，我们还会再次解释。

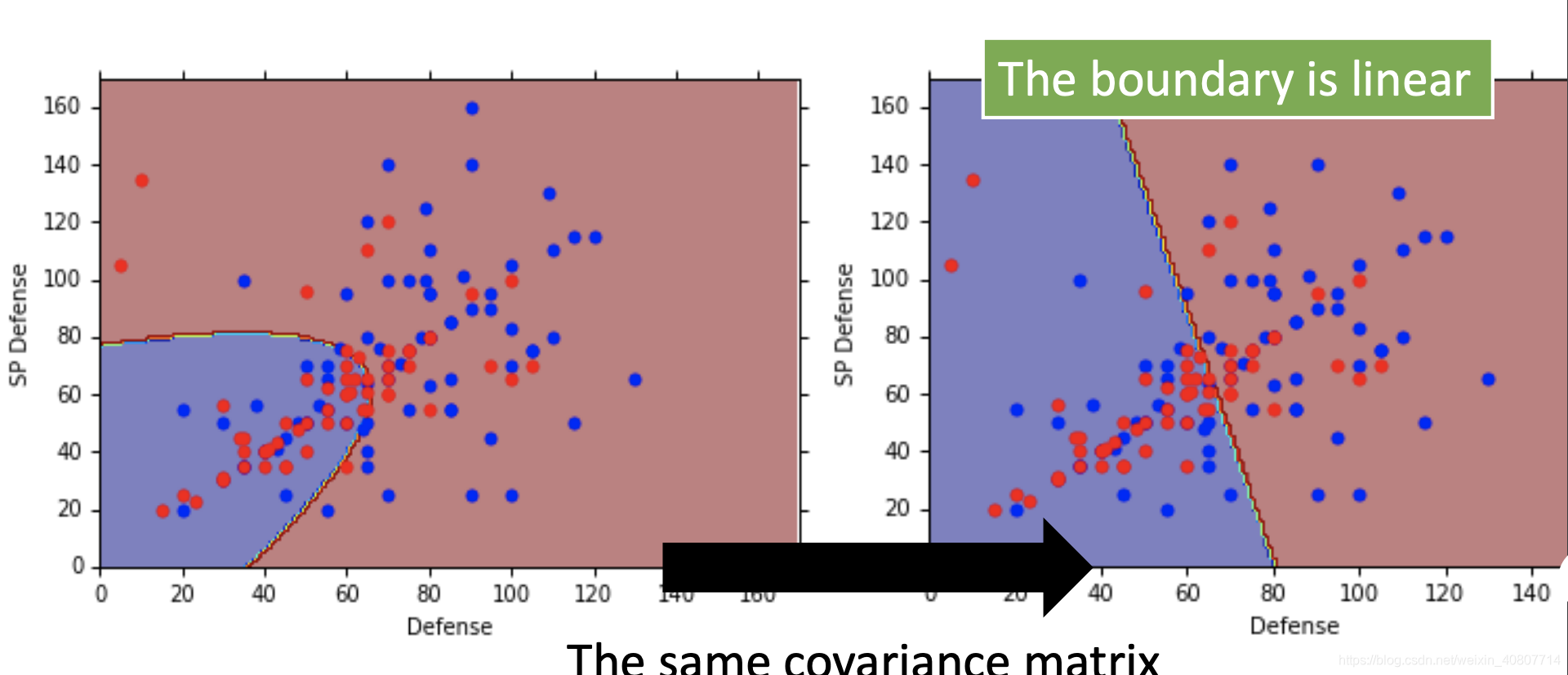
总结

  回到开篇的三步，开始修改：

1. Function(Model) :
   input : x -> $P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}$ -> output : class i
   当$P(C_1|x)>0.5$ , output : class 1
   else , output : class 2
2. Loss :
   评估高斯分布里的参数$\mu$和$\Sigma$。
   找到一个由$\mu$和$\Sigma$决定的概率分布，它可以最大化产生这些样本点的机率。
3. 找到最佳模型：极大似然估计。

关于概率分布的选择

  在概率生成模型中，我们假设样本点服从高斯分布。实际上，我们可以选择任何我们喜欢的概率分布。比如，对于binary features，我们可以假设样本点遵循伯努利分布。但不容忽视的一点是：参数少的分布，偏差大，方差小；模型复杂的分布，偏差小，方差大。

进一步拆解$P(x|C_1)$

  在刚才的分析中，我们一直在分析输入向量x的概率分布，但在实际应用中，我们的输入向量x由多个特征组成，每个特征组成向量x的维度，比如我们刚才就将向量推广到高维空间（7个特征）。那么需要我们进一步拆解$P(x|C_1)$！

线性判别分析

  接下来我们通过降维分类思想解读线性判别分析！基于数据进行分类时，一个很自然的想法是：将高维的数据降维至一维，然后使用某个阈值将各个类别分开。我们用二维特征举例，下面用图的形式展示：

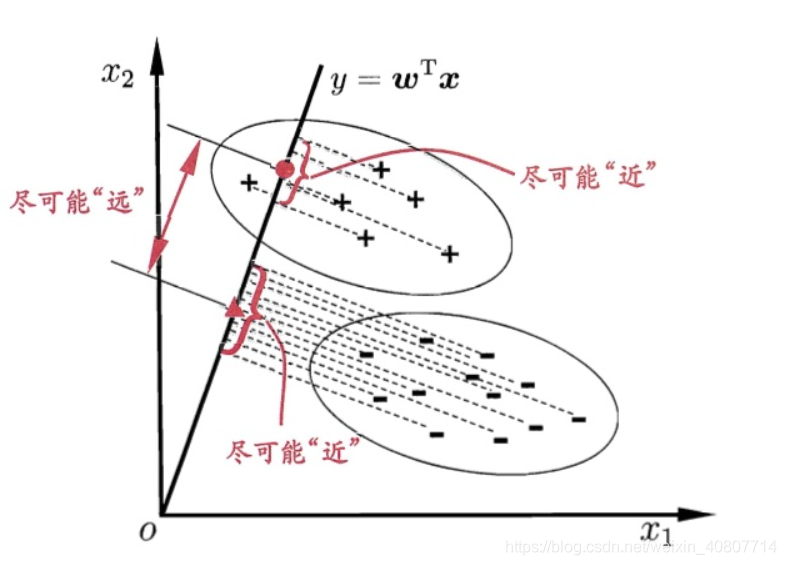
图中，数据的维度是二维的，我们的想法是把数据降维至一维，然后用阈值就能分类。这个似乎是一个很好的想法，我们总是希望降维后的数据同一个类别自身内部方差小，不同类别之间的方差要尽可能大。这也是合理的，因为同一个类别的数据应该更加相似，因此方差小；不同类别的数据之间应该很不相似，这样才能更容易对数据进行分类，我们简称为：类内方差小，类间方差大，在计算机语言叫“低耦合，高内聚”。在做具体的推导之前，我们对数据的形式和一些基本统计量做一些描述：
  特征$X=(x^1,x^2,...,x^N{)}^T$，因变量$Y=(y^1,y^2,...,y^N{)}^T$,其中$y_i\in +1,-1$。类别c1的特征$X_{c1}=x_i|y_i=+1$。同理，类别c2的特征$X_{c2}=x_i|y_i=-1$，属于c1类别的数据个数为$N_1$，属于类别c2的数据个数为$N_2$，其中$N_1+N_2=N$。

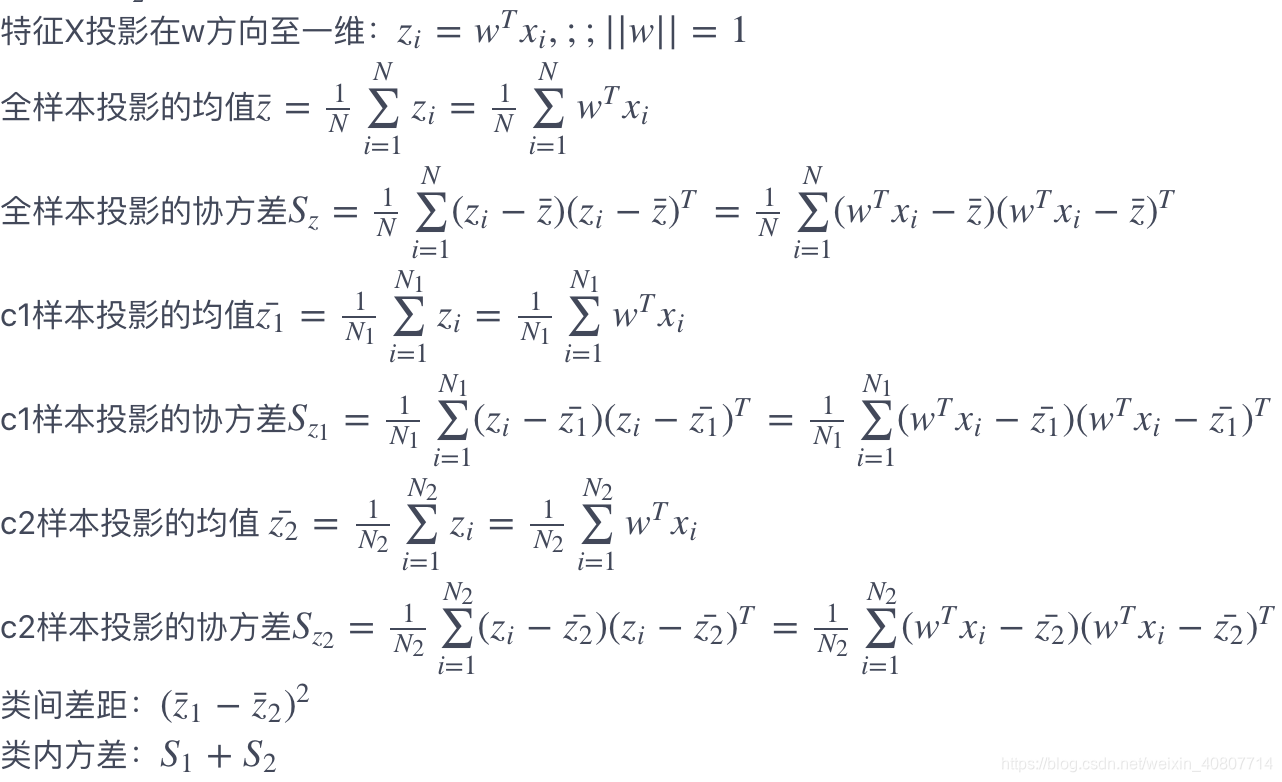
  由于线性判别分析的目标是同一类别内方差小，不同类别之间距离大，因此损失函数定义为：
$$\begin{gathered} J(w)=\frac{({\bar{z}}_1-{\bar{z}}_2{)}^2}{s_1+s_2}=\frac{w^T(\bar{x}{c}_1-\bar{x}{c}_2)(\bar{x}{c}_1-\bar{x}{c}_2{)}^{T}w}{w^T(s_{c_1}+s_{c_2})w} \\ \hat{w}=arg\underset{w}{\max }J(w) \end{gathered}$$

记：$S_b=(\bar{x}{c}_1-\bar{x}{c}_2)(\bar{x}{c}_1-\bar{x}{c}_2{)}^T,S_w=(s_{c_1}+s_{c_2})$，因此$J(w)=\frac{w^T{S}_{b}w}{w^T{S}_{w}w}$让$J(w)$对w求导等于0，求出：$w=S_w^{-1}(\bar{x}{c}_1-\bar{x}{c}_2)$

实践

数据准备

  接下来开始实践，收集数据集并选择合适的特征：在数据集上我们使用我们比较熟悉的IRIS鸢尾花数据集。

from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
feature = iris.feature_names
data = pd.DataFrame(X,columns=feature)
data['target'] = y
data.head()

  各个特征的相关解释：

• sepal length (cm)：花萼长度(厘米)
• sepal width (cm)：花萼宽度(厘米)
• petal length (cm)：花瓣长度(厘米)
• petal width (cm)：花瓣宽度(厘米)

度量模型性能

  度量分类模型的指标和回归的指标有很大的差异，首先是因为分类问题本身的因变量是离散变量，因此像定义回归的指标那样，单单衡量预测值和因变量的相似度可能行不通。其次，在分类任务中，我们对于每个类别犯错的代价不尽相同，例如：我们将癌症患者错误预测为无癌症和无癌症患者错误预测为癌症患者，在医院和个人的代价都是不同的，前者会使得患者无法得到及时的救治而耽搁了最佳治疗时间甚至付出生命的代价，而后者只需要在后续的治疗过程中继续取证就好了，因此我们很不希望出现前者，当我们发生了前者这样的错误的时候会认为建立的模型是很差的。为了解决这些问题，我们必须将各种情况分开讨论，然后给出评价指标。

• 真阳性TP：预测值和真实值都为正例；
• 真阴性TN：预测值与真实值都为正例；
• 假阳性FP：预测值为正，实际值为负；
• 假阴性FN：预测值为负，实际值为正；

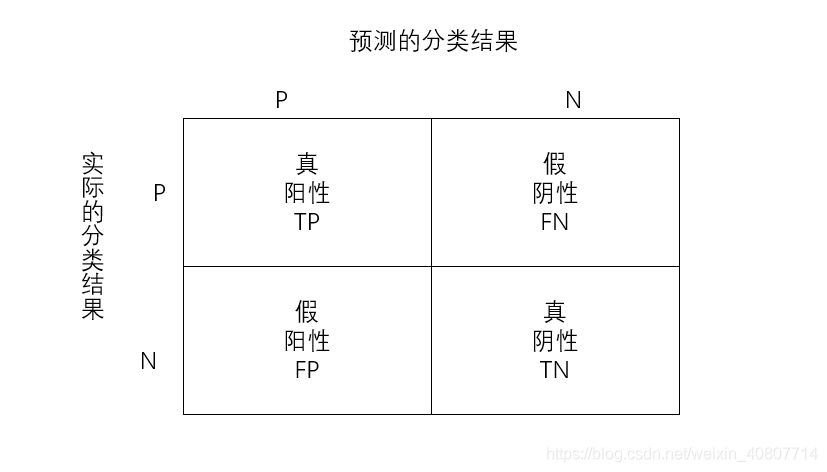
  分类模型的指标：

• 准确率：分类正确的样本数占总样本的比例，即：$ACC=\frac{TP+TN}{FP+FN+TP+TN}$.
• 精度：预测为正且分类正确的样本占预测值为正的比例，即：$PRE=\frac{TP}{TP+FP}$.
• 召回率：预测为正且分类正确的样本占类别为正的比例，即：$REC=\frac{TP}{TP+FN}$.
• F1值：综合衡量精度和召回率，即：$F1=2\frac{PRE\times REC}{PRE+REC}$.
• ROC曲线：以假阳率为横轴，真阳率为纵轴画出来的曲线，曲线下方面积越大越好。

在本次小案例中，我们使用ROC曲线作为最终评价指标。下面选择线性判别分析进行训练：

模型训练

# 线性判别分析
'''
参数：
solver:{'svd'，'lsqr'，'eigen'}，默认='svd'
solver的使用，可能的值：
'svd'：奇异值分解（默认）。不计算协方差矩阵，因此建议将此求解器用于具有大量特征的数据。

'lsqr'：最小二乘解，可以与收缩结合使用。

'eigen'：特征值分解，可以与收缩结合使用。
'''
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda_iris = LinearDiscriminantAnalysis()
lda_iris.fit(X,y)
lda_iris.score(X,y)

朴素贝叶斯分类

  如下图所示，假设所有特征都是独立的，我们不关心特征之间的协方差关系，这种分类方法就叫做朴素贝叶斯分类。

  在线性判别分析中，我们假设每种分类类别下的特征遵循同一个协方差矩阵，每两个特征之间是存在协方差的，因此在线性判别分析中各种特征是不是独立的。但是，朴素贝叶斯算法对线性判别分析作进一步的模型简化，它将线性判别分析中的协方差矩阵中的协方差全部变成0，只保留各自特征的方差，也就是朴素贝叶斯假设各个特征之间是不相关的。在之前所看到的偏差-方差理论中，我们知道模型的简化可以带来方差的减少但是增加偏差，因此朴素贝叶斯也不例外，它比线性判别分析模型的方差小，偏差大。虽然简化了模型，实际中使用朴素贝叶斯的案例非常多，甚至多于线性判别分析，例如鼎鼎大名的新闻分类，垃圾邮件分类等。

实践

模型训练

# 朴素贝叶斯             
from sklearn.naive_bayes import GaussianNB
NB_iris = GaussianNB()
NB_iris.fit(X, y)
NB_iris.score(X,y)

后验概率

  下面推导后验概率$P(C_1|x)$：
$$\begin{gathered} P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)} \\ =\frac{1}{1+\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}} \\ =\frac{1}{1+e^{-z}} \\ =\sigma (z) \end{gathered}$$
其中$z=ln\frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)}$.显然，这就是我们熟知的sigmod函数，函数图像如下：

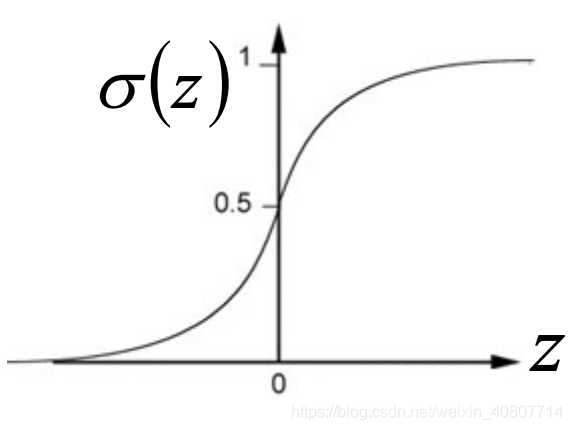
  进一步推导$P(C_1|x)=\sigma (z)$：
$$z=ln\frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)}=ln\frac{P(x|C_1)}{P(x|C_2)}+ln\frac{P(C_1)}{P(C_2)}$$
其中，令$N_1$表示class 1出现在训练集的次数，$N_2$表示class 2出现在训练集的次数，推出$\frac{P(C_1)}{P(C_2)}=\frac{\frac{N_1}{N_1+N_2}}{\frac{N_2}{N_1+N_2}}=\frac{N_1}{N_2}$。此外，
P ( x ∣ C 1 ) = 1 ( 2 π ) D 2 1 ∣ Σ 1 ∣ 1 2 e x p { − 1 2 ( x − μ 1 ) T ( Σ 1 ) − 1 ( x − μ 1 ) } P ( x ∣ C 2 ) = 1 ( 2 π ) D 2 1 ∣ Σ 2 ∣ 1 2 e x p { − 1 2 ( x − μ 2 ) T ( Σ 2 ) − 1 ( x − μ 2 ) } P(x|C_1)=\frac{1}{(2\pi)^{\frac{D}{2}}} \frac{1}{|\Sigma^1|^\frac{1}{2}}exp\{ -\frac{1}{2}(x-\mu^1)^T (\Sigma^1)^{-1} (x-\mu^1) \} \\ P(x|C_2)=\frac{1}{(2\pi)^{\frac{D}{2}}} \frac{1}{|\Sigma^2|^\frac{1}{2}}exp\{ -\frac{1}{2}(x-\mu^2)^T (\Sigma^2)^{-1} (x-\mu^2) \} P(x∣C1​)=(2π)2D​1​∣Σ1∣21​1​exp{−21​(x−μ1)T(Σ1)−1(x−μ1)}P(x∣C2​)=(2π)2D​1​∣Σ2∣21​1​exp{−21​(x−μ2)T(Σ2)−1(x−μ2)}
进一步化简左半部分
l n P ( x ∣ C 1 ) P ( x ∣ C 2 ) = l n ∣ Σ 2 ∣ 1 2 ∣ Σ 1 ∣ 1 2 e x p { − 1 2 ( x − μ 1 ) T ( Σ 1 ) − 1 ( x − μ 1 ) − 1 2 ( x − μ 2 ) T ( Σ 2 ) − 1 ( x − μ 2 ) } = l n ∣ Σ 2 ∣ 1 2 ∣ Σ 1 ∣ 1 2 − 1 2 [ ( x − μ 1 ) T ( Σ 1 ) − 1 ( x − μ 1 ) − ( x − μ 2 ) T ( Σ 2 ) − 1 ( x − μ 2 ) ] ln\frac{P(x|C_1)}{P(x|C_2)}=ln\frac{|\Sigma^2|^\frac{1}{2}}{|\Sigma^1|^\frac{1}{2}}exp\{ -\frac{1}{2}(x-\mu^1)^T (\Sigma^1)^{-1} (x-\mu^1) - \frac{1}{2}(x-\mu^2)^T (\Sigma^2)^{-1} (x-\mu^2) \} \\ =ln\frac{|\Sigma^2|^\frac{1}{2}}{|\Sigma^1|^\frac{1}{2}}-\frac{1}{2}[(x-\mu^1)^T (\Sigma^1)^{-1} (x-\mu^1)-(x-\mu^2)^T (\Sigma^2)^{-1} (x-\mu^2)] lnP(x∣C2​)P(x∣C1​)​=ln∣Σ1∣21​∣Σ2∣21​​exp{−21​(x−μ1)T(Σ1)−1(x−μ1)−21​(x−μ2)T(Σ2)−1(x−μ2)}=ln∣Σ1∣21​∣Σ2∣21​​−21​[(x−μ1)T(Σ1)−1(x−μ1)−(x−μ2)T(Σ2)−1(x−μ2)]
其中，$(x-{\mu }^1{)}^T({\Sigma }^1{)}^{-1}(x-{\mu }^1)=x^T({\Sigma }^1{)}^{-1}x-x^T({\Sigma }^1{)}^{-1}{\mu }^1-({\mu }^1{)}^T({\Sigma }^1{)}^{-1}x+({\mu }^1{)}^T({\Sigma }^1{)}^{-1}{\mu }^1$。观察等式右侧中间两项，我们发现均为常数$a$，对于实数$a$，$a^T=a$，即$(x^T({\Sigma }^1{)}^{-1}{\mu }^1{)}^T=({\mu }^1{)}^T({\Sigma }^1{)}^{-1}x$。继续化简：$(x-{\mu }^1{)}^T({\Sigma }^1{)}^{-1}(x-{\mu }^1)=x^T({\Sigma }^1{)}^{-1}x-2({\mu }^1{)}^T({\Sigma }^1{)}^{-1}x+({\mu }^1{)}^T({\Sigma }^1{)}^{-1}{\mu }^1$.
得到最终结果：
$$z=ln\frac{|{\Sigma }^2{|}^{\frac{1}{2}}}{|{\Sigma }^1{|}^{\frac{1}{2}}}-\frac{1}{2}{x}^T({\Sigma }^1{)}^{-1}x+({\mu }^1{)}^T({\Sigma }^1{)}^{-1}x-\frac{1}{2}({\mu }^1{)}^T({\Sigma }^1{)}^{-1}{\mu }^1+\frac{1}{2}{x}^T({\Sigma }^2{)}^{-1}x-({\mu }^2{)}^T({\Sigma }^2{)}^{-1}x+\frac{1}{2}({\mu }^2{)}^T({\Sigma }^2{)}^{-1}{\mu }^2+ln\frac{N_1}{N_2}$$

  在改进模型中，我们提出不同的class要共享同一个协方差矩阵，因此我们可以假设$\Sigma ={\Sigma }^1={\Sigma }^2$，代入$z$得出：
$$z=({\mu }^1-{\mu }^2{)}^T{\Sigma }^{-1}x-\frac{1}{2}({\mu }^1{)}^T({\Sigma }^1{)}^{-1}{\mu }^1+\frac{1}{2}({\mu }^2{)}^T({\Sigma }^2{)}^{-1}{\mu }^2+ln\frac{N_1}{N_2}$$
通过观察，我们发现x前系数是列向量的转置，x后的系数整体为一个常数。不妨设
$$\begin{gathered} w^T=({\mu }^1-{\mu }^2{)}^T{\Sigma }^{-1} \\ b=-\frac{1}{2}({\mu }^1{)}^T({\Sigma }^1{)}^{-1}{\mu }^1+\frac{1}{2}({\mu }^2{)}^T({\Sigma }^2{)}^{-1}{\mu }^2+ln\frac{N_1}{N_2} \end{gathered}$$
即：
$$z=w^{T}x+b$$
得出最终结果：
$$P(C_1|x)=\sigma (w\cdot x+b)$$
非常amazing！我们又回到了基本的线性回归模型。我们可以直观地理解，在共用$\Sigma$之后，class 1和class 2的分界是线性的。这也解释了为什么说基于概率的分类模型是线性模型！

疑问

  经历了上一节大篇幅的公式推导后，我们最终将概率生成模型化简成了我们熟悉的样子～但是，我们理清一个逻辑关系，就是在概率生成模型中，我们需要找出$N_1,N_2,{\mu }^1,{\mu }^2,\Sigma$（以二分类为例），才能得出最终结果里的参数$w$和$b$。那么是否有一个种方法可以让我们直接得到参数$w$和$b$呢？接下来引出logistic regression（逻辑斯蒂回归）。

logistic regression

参考

• Datawhale集成学习项目地址
• 李宏毅ML20课程主页