数据挖掘07

数据挖掘07

一.时序数据挖掘概述

1.定义

按时间排列的观测数据的序列。

在进行数据挖掘时，必须考虑数据间存在的时间关系。

2.采样间隔

分为：

等间隔采样：采样间隔固定

非等间隔采样：采样间隔有变化

答案：ABD

答案：C

二、锁步度量方法

锁步（Lockstep）对齐指的是：两个时间序列在比较时，第 i 个点只能与另一个序列的第 i 个点对齐，不允许时间轴上的伸缩、压缩或偏移。

这种对齐方式也称为逐点对齐（point-wise alignment）或刚性对齐（rigid alignment）。

欧氏距离（Euclidean Distance）就是典型的锁步度量方法。

公示如下：

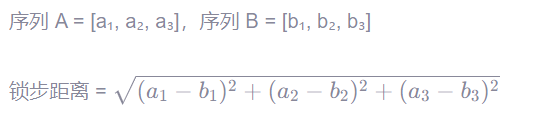
例题：

答案：BC

缺点：

在未预对齐的时间序列上直接使用锁步度量，会导致语义上不对应的点被比较，从而产生误导性结果。

例子：

同一个人说两次你好，语速不同。

此时欧氏距离在这种情况下会失效，因为强制 i↔i 对齐。

所以，我们想要找到两个时间序列之间最佳的对齐方式，使得
形态相似但是时序不对齐的两段序列通过缩放、平移等手段实现匹配。

于是引出DTW方法。

三.DTW方法（动态时间规整方法）

1.定义

DTW（Dynamic Time Warping，动态时间规整） 是一种用于衡量两个时序序列相似度的算法，特别适用于长度不同、速度不一致或存在时间偏移的时间序列。

2.核心思想

允许时间轴非线性拉伸/压缩，以找到最佳对齐方式，使两个序列的距离最小。

3.算法流程

假设：

步骤 1：构建距离矩阵（Cost Matrix）

计算每对点的局部距离（通常用欧氏距离或绝对差）：

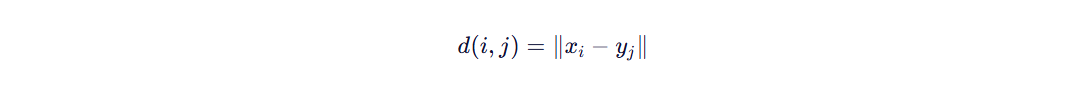
形成一个 n×m 的矩阵。

步骤 2：构建累积代价矩阵 D

使用动态规划递推：

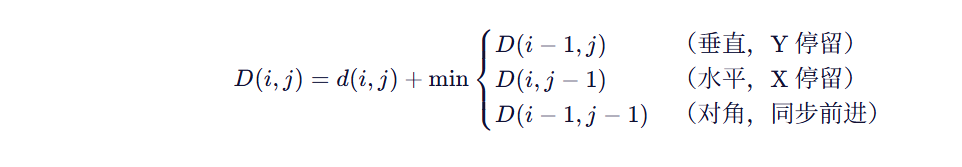
步骤 3：回溯得到最优路径

步骤 4：返回最小总距离

时间复杂度：O(nm)（无约束）
空间复杂度：O(nm)（存储整个矩阵），可优化至 O(min(n,m))（只存两行）

4.例子

第一步：计算局部距离矩阵 d(i,j)

使用绝对差作为点间距离（也可用平方差）：

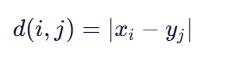
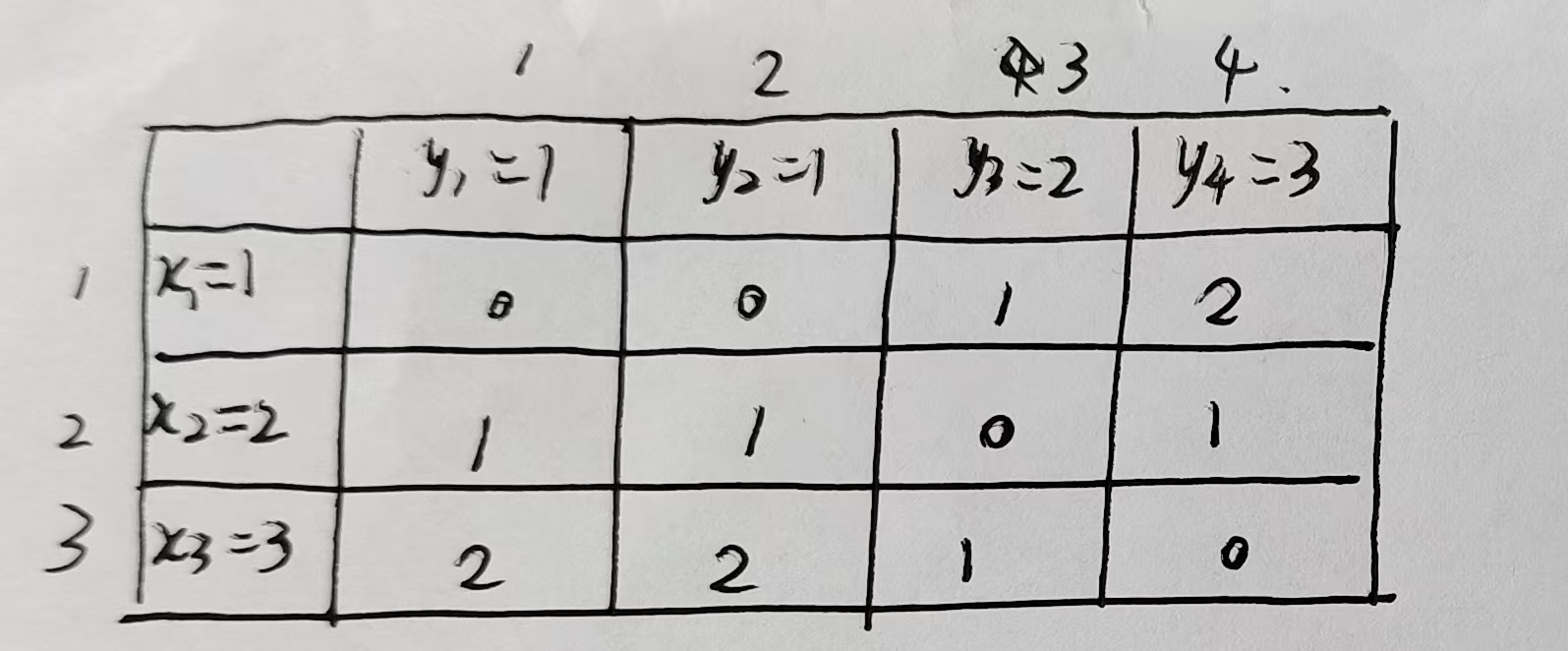
第二步：构建累积代价矩阵 D(i,j)

第一行：

D[1][1]=d(1,1)+min(D[0][1],D[1][0],D[0][0])=0+min(∞,∞,0)=0

D[1][2]=d(1,2)+min(D[0][2],D[1][1],D[0][1])=0+min(∞,0,∞)=0

D[1][3]=1+min(∞,D[1][2]=0,∞)=1+0=1

D[1][4]=2+min(∞,D[1][3]=1,∞)=2+1=3

第二行：

D[2][1] = d(2,1)=1 + min(D[1][1]=0, ∞, ∞) = 1 + 0 = 1

D[2][2] = 1 + min(D[1][2]=0, D[2][1]=1, D[1][1]=0) = 1 + 0 = 1

D[2][3] = 0 + min(D[1][3]=1, D[2][2]=1, D[1][2]=0) = 0 + 0 = 0

D[2][4] = 1 + min(D[1][4]=3, D[2][3]=0, D[1][3]=1) = 1 + 0 = 1

第三行：

D[3][1] = 2 + min(D[2][1]=1, ∞, ∞) = 2 + 1 = 3

D[3][2] = 2 + min(D[2][2]=1, D[3][1]=3, D[2][1]=1) = 2 + 1 = 3

D[3][3] = 1 + min(D[2][3]=0, D[3][2]=3, D[2][2]=1) = 1 + 0 = 1

D[3][4] = 0 + min(D[2][4]=1, D[3][3]=1, D[2][3]=0) = 0 + 0 = 0

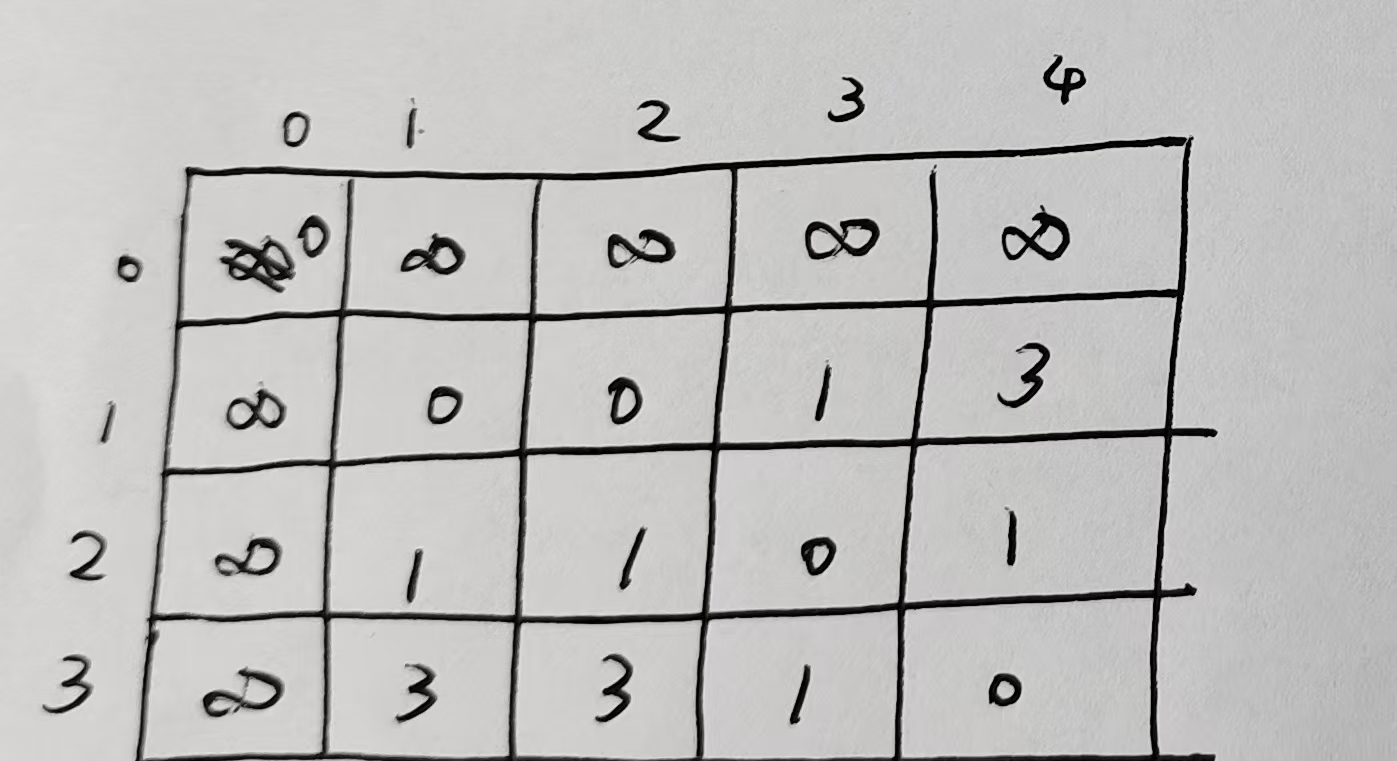
第三步：回溯最优对齐路径（Warping Path）

DTW 距离 = D[3][4] = 0

(3,4): 值=0，来自 d(3,4)=0 + D[2][3]=0 → 前驱是 (2,3)

(2,3): 值=0，来自 d(2,3)=0 + D[1][2]=0 → 前驱是 (1,2)

(1,2): 值=0，来自 d(1,2)=0 + D[1][1]=0 → 前驱是 (1,1)

所以是：

(1,1) → (1,2) → (2,3) → (3,4)

对齐解释：
x₁=1 ↔ y₁=1 和 y₂=1（X 的第一个点匹配 Y 的前两个点）
x₂=2 ↔ y₃=2
x₃=3 ↔ y₄=3

实现X与Y的后三个匹配。

5.DTW存在的问题

（1）问题：病态匹配

**“DTW 的病态匹配”（Pathological or Degenerate Warping）**是指动态时间规整（DTW）算法在某些情况下产生的不合理、过度扭曲、语义错误但数学上最优的对齐路径。

这类匹配虽然使累积距离最小，却严重违背了实际应用场景中的时序逻辑或物理意义，因此被称为“病态”。

（2）原因：不限制匹配路径生成的范围

没有限制路径可以偏离主对角线多远，这会导致：

1）序列 X 的第 1 个点可以匹配 Y 的最后 100 个点；

2）Y 的中间一段可以完全被“跳过”（通过垂直移动）；

3）路径可以极度弯曲，形成“L”形、“Z”形等。

这就会导致:

1)病态匹配（Pathological warping）

2)语义错误对齐

3)对噪声敏感

4)非物理对齐

（3）解决方法：

Sakoe-Chiba Band（最常用）：

限制路径不能偏离主对角线超过 窗口半宽 r

**

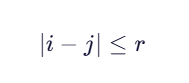
6.题目

**

答案：B

解释：

B是经典的 DTW-KNN 方法。选择最近的5个样本（k=5），按多数票决定类别。简单有效，广泛用于时间序列分类。
A 加权投票可以提升精度，但“前n个”太模糊，未指定具体数量（如k=5）。虽然合理，但不如B明确、标准。
CD选取最远的样本，显然不对。