波动方程，拉梅常数和赫姆霍兹方程

最新推荐文章于 2024-03-24 15:38:38 发布
最新推荐文章于 2024-03-24 15:38:38 发布
阅读量4.7k 收藏 12
点赞数 1
分类专栏： Mechanics
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/wanjiac/article/details/108312048
版权

以下内容主要整理自wiki，这是一个复杂的问题，很难一言以蔽之，根据个人情况，简单备忘如下。具体内容还是需要细学。

拉梅常数

之所以采用拉梅常数，因为有利于统一物理方程的表达形式。以下以均质各项同性弹性体为例，注意理解拉梅常数和常用的弹性参数之间的换算关系！

波动方程

标准波动方程

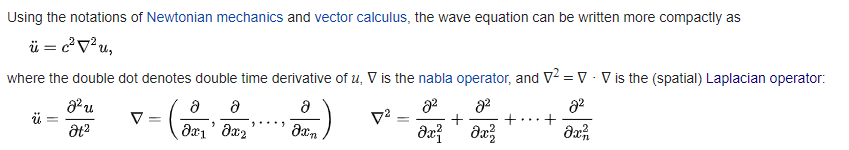
在线弹性理论，u为位移，c为介质中的波速，如剪切波波速c_{s}=\sqrt{\frac{G}{\rho}}，压缩波波速 c_{p}=\sqrt{\frac{\lambda+2G}{\rho}}，\lambda和G为拉梅常数，G为剪切模量，\rho是密度

赫姆霍兹方程（Helmholtz Equation）

注：要求变量不同时随时间和空间变化！对于地震动而言，要求是稳态问题。

参考资料

（1）拉梅常数（百科）;  Lamé parameters（wiki）

（2）波动方程（百科）;  Wave equation （wiki）

（3）波动方程（CSDN）

（4）Linear elasticity（wiki）

（5）豆艳萍,徐玉兰,汤忠飞.平面P波在自由界面上的反射[J].应用数学与计算数学学报,2011,25(01):80-89.（文章思路很清晰，值得学习！）

（6）Helmholzt Equation

ddd...e_bug
关注
  • 1
    点赞
  • 踩
  • 12
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
专栏目录
波动方程上海交通大学PPT
04-22
偏微分方程对计算机，金融等行业的发展均有重要意义，值得从业者学习。而偏微分方程中最重要的一类就是波动方程。本PPT是上海交大关于波动方程的精品PPT，深入浅出，祝君学习愉快！！~
拉梅曲线
weixin_30527323的博客
04-11 1012
拉梅曲线（Lamé curve）是在笛卡儿坐标系下满足以下方程式的点的集合，方程式为： 其中， 上述方程式的解会是一个在 的长方形内的封闭曲线，参数a和b称为曲线的半直径（semi-diameters）。 当 0<n<1 时，曲线形状类似一个四角星，四边的曲线往内凹； 当 n=1 时，曲线形状为菱形，四个顶点为(±a,0)及(0,±b)...
【高等传热学】拉梅系数
最新发布
KHQ_YJQ的博客
03-24 1689
在解决实际的导热问题时，首先需要选择适当的坐标系，以减少自变量的数目和便于边界条件的表达。例如，矩形区域中的问题可采用直角坐标系，而圆柱体中的导热则采用柱坐标系更为方便。如果在空间任一点处沿坐标轴方向的单位向量都两两垂直，则称该坐标系为正交坐标系。在推导正交坐标系下的导热微分方程时，需要知道微元弧长，以计算微元面积、微元体积。拉梅系数（也称尺度系数、度规系数），是在直角坐标系中空间曲线弧长的微分和在其他正交坐标系中空间曲线弧长的微分之间的比例系数。
[普通物理]波动方程
qq_51533157的博客
06-20 1389
振动方程
【GAMES201学习笔记】线性有限元
捕鱼维的个人小站
06-15 1232
《GAMES201》 学习笔记
波动方程有限差分
03-09
波动方程方法提出；有限差分的建立；二维有限差分的建立
储层砂岩波阻抗及拉梅常数实验研究 (2006年)
04-26
地层条件下应用岩石物理参数测试系统(MTS)测试了岩石纵横波速度，结合已研究成果，根据实验数据和计算结果总结了波阻抗和拉梅常数与不同地层条件的关系，得到地表条件下岩样(饱气)的波阻抗随岩石孔隙度的增加而减小...
地下水常微分方程的解——线性水库模型的Comsol数值解
04-22
线性水库模型的Comsol数值解，可以与解析解对比。提供了comsol文件，与结果到处，入渗率为一个分段函数
拉梅舒帕达耶
02-09
移动应用程序开发-Android和IOS（React Native，Xamarin.forms）。 全栈开发 （HTML5，CSS3，Saas，Bootstrap，JavaScript，PHP，MySQL） MEAN / MERN堆栈开发 （React，TypeScript，ES6，Angular，NodeJS，...
基于拉梅解答的喷射混凝土当量厚度分析与应用
05-02
在弹性力学圆筒受均布载荷的拉梅解答的基础上,建立了干、湿喷混凝土在相同支护强度情况下的喷层外半径与喷射混凝土强度的关系,并结合实验室试验及工程实例进行计算。结果表明:在相同支护强度情况下,喷射混凝土强度与...
固体力学里的拉梅参数mu和流体力学的动力粘度mu是不是一回事？
beidou111的博客
03-23 574
最近思考一个问题： 固体力学里的拉梅参数mu和流体力学的动力粘度mu是不是一回事？ WIKI（拉梅常数的页面）上是这么说的 按照维基的说法：是一回事。 这么看来是一回事？ 等等，其中“（单位不同）”是指？ 答：如果说剪切模量就是第二拉梅常数的话 剪切模量 其单位是N/m^2 而动力粘度的单位是N s/m^2 这么看来粘度多了一个s。 然而。。。 在wiki的关于剪切模量的页面，又有这么一行 好家伙，现在矛盾了。有大佬能指点迷津吗？ ...
目前掌握的来自Gabriel Lamé的一些知识
Leslie Lee's blog includes programming in math, physics, and engineering.
07-10 1193
加布里埃尔·拉梅（Gabriel Lamé，1795年7月22日－1870年5月1日），法国数学家。 1. Lamé公式 1883年Lamé首次对厚壁圆筒进行应力分析，提出的应力计算公式叫做Lamé公式。这是在压力容器设计中提到的。 2. Lamé常数 σ_ij = λ*e_aa*δ_ij+ 2μ*e_ij λ μ就是Lamé常数，第二个常数通常写作G，称之为剪切模量。 δ_ij是克罗内克函数 e_aa = e_xx +e_yy+e_zz 称为单位体积的体积改变量；体应变；wiki上面称 体积变...
连续介质力学——Lamé参数
qq_40621963的博客
01-07 1060
参考文献：Kim, Theodore, and David Eberle. “Dynamic Deformables: Implementation and Production Practicalities (Now with Code!意味着无论它如何破环模拟的稳定性，都必须不惜一切代价保留体积。许多模拟器非得搞得老复杂（包括Fizt），不直接支持Lamé参数。描述需要多少相对长度和体积保留的参数，通常使用Lamé参数。如果需要保留大量体积，需要将。的泊松比，但它们并不完全等于。
弹性方法计算内力例题_弹性力学重要公式汇总，还不快来强记一波【含参考答案】...
weixin_35160622的博客
01-03 5625
考生对满分的向往，就是我们的奋斗目标！!还记得上次我们留给大家的弹性力学填空题吗？今天给大家提供参考答案。弹性力学重要公式复习检测(请填空)弹性力学重要公式总结(含答案)弹性力学的基本方程(空间直角坐标)1．平衡微分方程：(3个)【参考答案】2．几何方程(6个)【参考答案】3．物理方程：(6个)【参考答案】4．用应变表示应力(6个)【参考答案】按位移求解：5．弹性方程...
波动方程
热门推荐
痞子龙3D编程
09-25 3万+
波动方程 根据波动方程的建模，一个脉冲在一根固定两端的绳子上的运动   从一个点源发散出的球面波 波动方程或称波方程（英语：wave equation）是一种重要的偏微分方程，主要描述自然界中的各种的波动现象，包括横波和纵波，例如声波、光波和水波。波动方程抽象自声学，电磁学，和流体力学等领域。 历史上许多科学家，如达
固体的弹性性质
define_us的专栏
12-21 2147
（1）应力和应变 应力的单位和压强相同。 将固体在直角坐标系x1，x2，x3,中划分为体积可以忽略的正方体体积元，设物体受力为Fij，其中，i为所受力的面，j为所受力的方向。 所以体积元共受9个力，可以写成3*3的矩阵，其中F(i,j)=F(j,i),在这里不做证明，所以一共有6个独立分量。 （2）广义胡克定律 F(i,j)=c(i,j,k,l)*e(k,l)
怎么推导亥姆霍兹方程
weixin_35755562的博客
01-09 1376
亥姆霍兹方程(Heisenberg uncertainty principle)是一个物理学定理，由德国物理学家亥姆霍兹在1927年提出。这个定理描述了一个粒子的位置和动量之间的关系，即在观测这个粒子的位置时，我们无法精确测量它的动量，反之亦然。 亥姆霍兹方程可以表示为： Δx⋅Δp≥ℏ/2 其中，Δx表示粒子位置的不确定度，Δp表示粒子动量的不确定度，ℏ是普朗克常数的一半。 这个方程表明，在观测...
拉梅系数以及雅克比行列式
帅气廖鹏飞
06-06 1万+
u1,u2,u3u1,u2,u3u_1,u_2,u_3分别是三个坐标，h1,h2,h3h1,h2,h3h_1,h_2,h_3就是拉梅系数 圆柱坐标： u1=ρ,u2=ϕ,u3=zu1=ρ,u2=ϕ,u3=zu_1=\rho,u_2=\phi,u_3=z h1=1,u2=ρ,u3=1h1=1,u2=ρ,u3=1h_1=1,u_2=\rho,u_3=1 球坐标：（ϕ是2π那个角ϕ是2π那个角\...
已知岩石样品的密度为ρ=2g/cm3,比热容为C=0.75,热传导系数为K=4.4,假设岩石对光吸收率为η=0.6,初始温度T0＝300K．利用matlab根据拉普拉斯求沿x轴速度v移动的基模高斯激光辐照岩石温度场，再根据热位移平衡方程求得应力场
04-03
由于题目中没有给出岩石的尺寸和形状，因此在求解过程中需要假设岩石为无限大的均匀介质。 首先，根据高斯光束的定义可以得到其强度分布函数： $$ I(x,y,z) = I_0 \exp \left[-\frac{2(x^2+y^2)}{w_0^2}\right] $$ 其中，$I_0$为光束中心的强度，$w_0$为光束半径。由于高斯光束在传播过程中会发生自聚焦，因此光束在岩石内部的强度分布函数也会发生改变。为了考虑这个因素，可以采用传输矩阵法计算光束在岩石内部的传播过程。具体来说，可以将岩石划分成若干个平行于x轴的薄层，每一层的厚度为$\Delta z$，在每一层中计算光束的传输矩阵$M$，然后逐层计算光束的强度分布函数。传输矩阵的计算公式为： $$ M = \begin{bmatrix} 1 & \Delta z \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ -\frac{1}{f}\Delta z & 1 \end{bmatrix} \begin{bmatrix} 1 & \Delta z \\ 0 & 1 \end{bmatrix} $$ 其中，$f$为光束的焦距。在计算传输矩阵时，可以采用近似公式： $$ M \approx \begin{bmatrix} 1-\frac{\Delta z}{f} & \Delta z \\ -\frac{1}{f}\Delta z & 1-\frac{\Delta z}{f} \end{bmatrix} $$ 接下来，可以根据光束的强度分布函数计算岩石中的吸收能量密度$Q$： $$ Q(x,y,z) = \eta I(x,y,z) $$ 其中，$\eta$为岩石的光吸收率。由于高斯光束的强度分布函数具有轴对称性，因此可以将岩石的吸收能量密度简化为一维问题： $$ q(x,z) = \int_{-\infty}^{+\infty} Q(x,y,z) dy = 2\eta I_0 e^{-\frac{2x^2}{w_0^2}} $$ 由于岩石是均匀介质，因此其热传导方程可以写为： $$ \frac{\partial T}{\partial t} = \frac{K}{\rho C} \nabla^2 T + \frac{Q}{\rho C} $$ 其中，$T$为岩石的温度，$\rho$为岩石的密度，$C$为岩石的比热容，$K$为岩石的热传导系数。由于岩石是无限大的均匀介质，因此可以将热传导方程简化为一维问题： $$ \frac{\partial T}{\partial t} = \frac{K}{\rho C} \frac{\partial^2 T}{\partial x^2} + \frac{q(x,t)}{\rho C} $$ 在数值求解过程中，可以采用有限差分法对上式进行离散化。将时间和空间分别离散为$t_n=n\Delta t$和$x_i=i\Delta x$，则上式可以写为： $$ \frac{T_{i,n+1}-T_{i,n}}{\Delta t} = \frac{K}{\rho C} \frac{T_{i+1,n}-2T_{i,n}+T_{i-1,n}}{\Delta x^2} + \frac{q_{i,n}}{\rho C} $$ 将上式变形，可以得到关于$T_{i,n+1}$的迭代公式： $$ T_{i,n+1} = T_{i,n} + \frac{K\Delta t}{\rho C\Delta x^2} (T_{i+1,n}-2T_{i,n}+T_{i-1,n}) + \frac{\Delta t}{\rho C} q_{i,n} $$ 上式中的$q_{i,n}$可以根据前面计算的吸收能量密度$q(x,z)$和传输矩阵$M$得到。具体来说，可以先计算光束在岩石中的传输矩阵$M(z)$，然后利用传输矩阵将光束的强度分布函数转化到每一层的位置上，最后计算吸收能量密度$q(x,z)$。 在求解温度场之后，可以根据热位移平衡方程求解应力场。热位移平衡方程可以写为： $$ \rho \frac{\partial^2 u}{\partial t^2} = \nabla \cdot \sigma $$ 其中，$u$为岩石的位移场，$\sigma$为应力张量。由于岩石的形变很小，因此可以采用线弹性理论来计算应力张量： $$ \sigma_{ij} = \lambda \delta_{ij} \epsilon_{kk} + 2\mu \epsilon_{ij} $$ 其中，$\lambda$和$\mu$为岩石的拉梅常数，$\delta_{ij}$为Kronecker delta符号，$\epsilon_{ij}$为应变张量。应变张量可以根据位移场求解得到： $$ \epsilon_{ij} = \frac{1}{2} \left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right) $$ 将上述公式代入热位移平衡方程，可以得到关于$u_{i,n+1}$的迭代公式： $$ u_{i,n+1} = 2u_{i,n} - u_{i,n-1} + \frac{\Delta t^2}{\rho} \left(\frac{\sigma_{i+1/2,n}-\sigma_{i-1/2,n}}{\Delta x}\right) $$ 其中，$\sigma_{i+1/2,n}$和$\sigma_{i-1/2,n}$可以根据前面计算的应变张量和岩石的材料参数求解得到。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值