【GAMES201学习笔记】线性有限元

1. 形变参数

1.1 形变映射

形变映射 $\varphi$ ：静止材料位置 $\mapsto$ 形变材料位置

$${\mathbf{x}}_{\mathbf{deformed}}=\varphi ({\mathbf{x}}_{\mathbf{rest}})$$

1.2 形变梯度

形变梯度 $\mathbf{F}$ ：

$$\mathbf{F}:=\frac{\partial {\mathbf{x}}_{\mathbf{deformed}}}{\partial {\mathbf{x}}_{\mathbf{rest}}}$$

Note ：

• 平移过程中形变梯度保持不变：${\varphi }_1=\varphi ({\mathbf{x}}_{\mathbf{rest}})$ 和 ${\varphi }_1=\varphi ({\mathbf{x}}_{\mathbf{rest}})+c$ 有相同的形变梯度

1.3 变形/静止体积比

变形/静止体积比 $J$ ：

$$J=\det (\mathbf{F})$$

Note ：

• 三维空间中，矩阵行列式的性质，即体积变化倍数

2. 弹性体

2.1 超弹性体（Hyperelasticity）

超弹性材料：应力 – 应变关系 由 应变能密度函数 定义 ：

$$\Psi =\Psi (\mathbf{F})$$

直观理解：$\Psi$ 是惩罚形变的势函数。

应力 ：材料的内部弹性力。

应变 ：现在用 形变梯度 $\mathbf{F}$ 代替。

Note ：

• $\Psi$ 是应变能量密度函数
• $\varphi$ 是形变映射

2.2 应力张量

应力：代表材料微元施加在其周围为材料微元的内力。

2.2.1 三种常用的应力张量

• Piola - Kirchhoff 应力张量 （PK1）：
  $$\mathbf{P}(\mathbf{F})=\frac{\partial \Psi (\mathbf{F})}{\partial \mathbf{F}}$$
  （计算简单，是在静止空间计算，需要变换到形变空间）
   
• 基尔霍夫应力（Kirchhoff stress） ：$\tau$
   
• 柯西应力张量（Cauchy stress tensor） ：$\sigma$
  （对称，因为角动量守恒）

2.2.2 关系式

• $\tau =J\sigma ={\mathbf{PF}}^T$
• $\mathbf{P}=J\sigma {\mathbf{F}}^{-T}$

Note：

• ${\mathbf{F}}^{-T}$ ：补偿材料变形
• 用 ${\mathbf{F}}^{-T}$ 替代 ${\mathbf{F}}^{-1}$ ：因为变换的是法向量 $\mathbf{n}$ 而不是 $\mathbf{x}$

2.2.3 牵引力

• $\mathbf{t}={\sigma }^T\mathbf{n}$

直观来说，将法向量乘以应力张量即可获得材料向周围微元施加的力。

2.3 弹性模量（各向同性材料）

• 杨氏模量 ：应力张量与应变张量的比值
  $$E=\frac{\sigma }{ϵ}$$

• 体积模量 ：压强关于体积的变化，常用于液体
  $$K=-V\frac{dP}{dV}$$

• 泊松比 ：
  $$\nu \in [0.0,0.5)$$

Note ：

• 辅助项具有负泊松比；
• 泊松比为 0 时，拉长物体时，截面积不会发生变化；
• 泊松比较大时，物体会尽量保持体积不变，例如在拉长物体时，物体会变细。

拉梅常数（Lamé parameters） ：

• Lamé 第一参数： $\lambda$
  表示材料的压缩性，等价与体弹性模量或者杨氏模量
   
• Lamé 第二参数： $\mu$
  表示材料的剪切模量，用 G 表示

换算公式 ：

• $K=\frac{E}{3(1-2\nu )}$ （常用于可压缩液体）
   
• $\lambda =\frac{E\nu }{(1+\nu )(1-2\nu )}$
   
• $\mu =\frac{E}{2(1+\nu )}$

广义胡克定律 ：均匀和各向同性的材料

$$\sigma =2\mu ϵ+\lambda tr(ϵ)$$

3. 常见的超弹性模型

• 经典的 MPM 方法将每个粒子看做材料的一个微元，材料的本构模型会有一个能量密度函数 $\Psi$ ；
• 对能量密度函数 $\Psi$ 关于整个模型求积分，得到整个材料的势能；
• 势能对材料点的形变梯度进行求导：$P(\mathbf{F})=\frac{\partial \Psi }{\partial \mathbf{F}}$ ；
• 物理意义上来说，势能对位置求导的结果就是力，$P(\mathbf{F})$ 可以看做材料点的受力。

3.1 Neo-Hookean 模型

适用于各向同性材料

• $\Psi (\mathbf{F})=\frac{\mu }{2}{\sum }_i[({\mathbf{F}}^T\mathbf{F}{)}_{ii}-1]-\mu \log (J)+\frac{\lambda }{2}{\log }^2(J)$
   
• $P(\mathbf{F})=\frac{\partial \Psi }{\partial \mathbf{F}}=\mu (\mathbf{F}-{\mathbf{F}}^T)+\lambda \log (J){\mathbf{F}}^{-T}$

因为 Neo-Hookean 模型容易造成能量流失，这时可以考虑 Corotated 模型。

FEM 中应用 Neo-Hookean 模型的示例代码 ：

dim = 2

E, nu = 1000, 0.3
la = E * nu / ((1 + nu) * (1 - 2 * nu))
mu = E / (2 * (1 + nu))

element_V = 0.01

pars = ti.Vector(dim, dt=real, shape=n_nodes, needs_grad=True)
vels = ti.Vector(dim, dt=real, shape=n_nodes)

total_energy = ti.var(dt=real, shape=(), needs_grad=True)

# 计算势能
@ti.kernel
def compute_total_energy():
    for i in range(n_elements):
        # get F：见 4.2
        ......
        # NeoHookean
        I1 = (F @ F.transpose()).trace()
        # 防止 J 的值过小引起错误
        J = max(0.2, F.determinant())
        element_energy_density = 0.5 * mu * (I1 - dim) - mu * ti.log(J) + 0.5 * la * ti.log(J)**2
        total_energy[None] += element_energy_density * element_V

# 渲染循环
while True:
    for s in range(30):
        # 调用 taichi 的自动微分器
        # 定义的损失函数：compute_total_energy()
        # 函数值：total_energy
        # 变量值：x
        # 微分结果(i 点上的力) ：x.grad[i]
        # f = - \partial (total_energy) / \partial x
        with ti.Tape(total_energy):
            compute_total_energy()
        ......

Note ：

• 在 FEM 中的势能（后续有详细说明）：

$$U(e)={\int }_e\mathbf{\Psi }(\mathbf{F}(\mathbf{x}))\mathrm{d}\mathbf{x}=V_e\mathbf{\Psi }({\mathbf{F}}_{\mathbf{e}})$$

3.2 (Fixed)Corotated 模型

• $\Psi (\mathbf{F})=\mu {\sum }_i({\sigma }_i-1{)}^2+\frac{\lambda }{2}(J-1{)}^2$
   
• $P(\mathbf{F})=\frac{\partial \Psi }{\partial \mathbf{F}}=2\mu (\mathbf{F}-\mathbf{R})+\lambda (J-1)J{\mathbf{F}}^{-T}$

Note ：

• ${\sigma }_i$ 是 $\mathbf{F}$ 的奇异值。

3.3 MPM 教程

《The Material Point Method for Simulating Continuum Materials》

4. 有限元基础

有限元法 ：建立离散模型的 Galerkin 离散格式。

4.1 微元构建

4.1.1 三角形微元

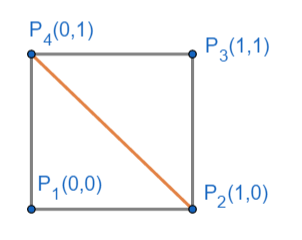
n_nodes_x
n_nodes_y
n_nodes = n_nodes_x * n_nodes_y
n_elements = (n_nodes_x - 1) * (n_nodes_y - 1) * 2

pars = ti.Vector(dim, dt=ti.f32, shape=n_nodes, needs_grad=True)
vels = ti.Vector(dim, dt=ti.f32, shape=n_nodes)
elements = ti.var(dt=ti.i32, shape=(n_elements, dim + 1))

# 微元体积
dx = 1 / 16

# 生成基准点的坐标
init_pos = [0.1, 0.7])

def genMesh():
    offset_x = 0.1

    get_pid = lambda i, j: i * n_nodes_y + j

    for i in range(n_nodes_x):
        for j in range(n_nodes_y):
            # particle id
            pid = get_pid(i, j)
            pars[pid] = [init_pos[0] + i * dx * 0.5, 
                         init_pos[1] + j * dx * 0.5 + i * dx * offset_x]
            vels[pid] = [0, -1]

    # build vertices
    for i in range(n_nodes_x - 1):
        for j in range(n_nodes_y - 1):
            # element id
            eid = (i * (n_nodes_y - 1) + j) * 2
            elements[eid, 0] = get_pid(i, j)
            elements[eid, 1] = get_pid(i + 1, j)
            elements[eid, 2] = get_pid(i, j + 1)

            eid = (i * (n_nodes_y - 1) + j) * 2 + 1
            elements[eid, 0] = get_pid(i + 1, j + 1)
            elements[eid, 1] = get_pid(i, j + 1)
            elements[eid, 2] = get_pid(i + 1, j)

4.1.2 四面体微元

TetGen_Cube.node

......
8  3  0  0
   1    0  0  0
   2    1  0  0
   3    1  1  0
   4    0  1  0
   5    0  0  1
   6    1  0  1
   7    1  1  1
   8    0  1  1

TetGen_Cube.ele

......
6  4  0
    1       6     7     1     5
    2       1     8     3     4
    3       3     7     1     2
    4       1     7     6     2
    5       1     7     3     8
    6       7     8     1     5

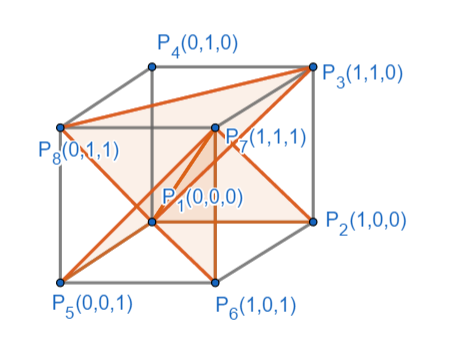
代码示例 ：

n_nodes_x
n_nodes_y
n_nodes_z
n_nodes = n_nodes_x * n_nodes_y * n_nodes_z
n_elements = (n_nodes_x - 1) * (n_nodes_y - 1) * (n_nodes_z - 1) * 6

pars = ti.Vector(dim, dt=ti.f32, shape=n_nodes, needs_grad=True)
vels = ti.Vector(dim, dt=ti.f32, shape=n_nodes)
elements = ti.var(dt=ti.i32, shape=(n_elements, dim + 1))

# 微元体积
dx = 1 / 16

# 生成基准点的坐标
init_pos = [0.0, 0.7, 0.0]

def genMeshP():
    get_pid = lambda i, j, k: i * n_nodes_y * n_nodes_z + j * n_nodes_z + k

    for i in range(n_nodes_x):
        for j in range(n_nodes_y):
            for k in range(n_nodes_z):
                # particle id
                pid = get_pid(i, j, k)
                pars[pid] = [init_pos[0] + i * dx * 0.5,
                             init_pos[1] + j * dx * 0.5,
                             init_pos[2] + k * dx * 0.5]
                vels[pid] = [0, -1, 0]

    # build vertices
    for i in range(n_nodes_x - 1):
        for j in range(n_nodes_y - 1):
            for k in range(n_nodes_z - 1):
                # particle id
                # 1 (i, j, k)
                # 2 (i + 1, j, k)
                # 3 (i + 1, j + 1, k)
                # 4 (i, j + 1, k)
                # 5 (i, j, k + 1)
                # 6 (i + 1, j, k + 1)
                # 7 (i + 1, j + 1, k + 1)
                # 8 (i, j + 1, k + 1)

                # element id
                # 0 {6, 7, 1, 5}
                eid = ((i * (n_nodes_y - 1) + j) * (n_nodes_z - 1) + k) * 6
                elements[eid, 0] = get_pid(i + 1, j, k + 1)
                elements[eid, 1] = get_pid(i + 1, j + 1, k + 1)
                elements[eid, 2] = get_pid(i, j, k)
                elements[eid, 3] = get_pid(i, j, k + 1)

                # 1 {1, 8, 3, 4}
                eid = ((i * (n_nodes_y - 1) + j) * (n_nodes_z - 1) + k) * 6 + 1
                elements[eid, 0] = get_pid(i, j, k)
                elements[eid, 1] = get_pid(i, j + 1, k + 1)
                elements[eid, 2] = get_pid(i + 1, j + 1, k)
                elements[eid, 3] = get_pid(i, j + 1, k)

                # 2 {3, 7, 1, 2}
                eid = ((i * (n_nodes_y - 1) + j) * (n_nodes_z - 1) + k) * 6 + 2
                elements[eid, 0] = get_pid(i + 1, j + 1, k)
                elements[eid, 1] = get_pid(i + 1, j + 1, k + 1)
                elements[eid, 2] = get_pid(i, j, k)
                elements[eid, 3] = get_pid(i + 1, j, k)

                # 3 {1, 7, 6, 2}
                eid = ((i * (n_nodes_y - 1) + j) * (n_nodes_z - 1) + k) * 6 + 3
                elements[eid, 0] = get_pid(i, j, k)
                elements[eid, 1] = get_pid(i + 1, j + 1, k + 1)
                elements[eid, 2] = get_pid(i + 1, j, k + 1)
                elements[eid, 3] = get_pid(i + 1, j, k)

                # 4 {1, 7, 3, 8}
                eid = ((i * (n_nodes_y - 1) + j) * (n_nodes_z - 1) + k) * 6 + 4
                elements[eid, 0] = get_pid(i, j, k)
                elements[eid, 1] = get_pid(i + 1, j + 1, k + 1)
                elements[eid, 2] = get_pid(i + 1, j + 1, k)
                elements[eid, 3] = get_pid(i, j + 1, k + 1)

                # 5 {7, 8, 1, 5}
                eid = ((i * (n_nodes_y - 1) + j) * (n_nodes_z - 1) + k) * 6 + 5
                elements[eid, 0] = get_pid(i + 1, j + 1, k + 1)
                elements[eid, 1] = get_pid(i, j + 1, k + 1)
                elements[eid, 2] = get_pid(i, j, k)
                elements[eid, 3] = get_pid(i, j, k + 1)

4.2 线性四面体（三角形）有限元法

线性四面体有限元（用于弹性）假设 形变映射 $phi$ 是一个仿射变换，因此 形变梯度 $\mathbf{F}$ 在单个四面体单元内是恒定的，对单个元素来说：

$${\mathbf{x}}_{\mathbf{deformed}}=\mathbf{F}{\mathbf{x}}_{\mathbf{rest}}+\mathbf{p}$$

对于每个元素 $e$ ，对能量密度函数求体积的积分，可以计算其弹性势能：

$$U(e)={\int }_e\mathbf{\Psi }(\mathbf{F}(\mathbf{x}))\mathrm{d}\mathbf{x}=V_e\mathbf{\Psi }({\mathbf{F}}_{\mathbf{e}})$$

• 其中 形变梯度 $\mathbf{F}$ 在元素 $e$ 上是个常数 ${\mathbf{F}}_{\mathbf{e}}$ ，即 $\mathbf{\Psi }({\mathbf{F}}_{\mathbf{e}})$ 也为常数，因此可以直接得到积分结果。

4.3 计算形变梯度

$${\mathbf{x}}_{\mathbf{deformed}}=\mathbf{F}{\mathbf{x}}_{\mathbf{rest}}+\mathbf{p}$$

在 2D 三角形元素（三维空间中是四面体元素）中，设：

• 静止时的顶点位置： ${\mathbf{a}}_{\mathbf{rest}}$ ，${\mathbf{b}}_{\mathbf{rest}}$ ，${\mathbf{c}}_{\mathbf{rest}}$ ；
• 变形后的顶点位置：${\mathbf{a}}_{\mathbf{deformed}}$ ，${\mathbf{b}}_{\mathbf{deformed}}$ ，${\mathbf{c}}_{\mathbf{deformed}}$ 。

因为在线性三角形元素中 $\mathbf{F}$ 是常数，则有：

$$\begin{array}{rl}{\mathbf{a}}_{\mathbf{deformed}}& =\mathbf{F}{\mathbf{a}}_{\mathbf{rest}}+\mathbf{p}\\ {\mathbf{b}}_{\mathbf{deformed}}& =\mathbf{F}{\mathbf{b}}_{\mathbf{rest}}+\mathbf{p}\\ {\mathbf{c}}_{\mathbf{deformed}}& =\mathbf{F}{\mathbf{c}}_{\mathbf{rest}}+\mathbf{p}\end{array}$$

消除 $\mathbf{p}$ ：

$$\begin{array}{rl}({\mathbf{a}}_{\mathbf{deformed}}-{\mathbf{c}}_{\mathbf{deformed}})& =\mathbf{F}({\mathbf{a}}_{\mathbf{rest}}-{\mathbf{c}}_{\mathbf{rest}})\\ ({\mathbf{b}}_{\mathbf{deformed}}-{\mathbf{c}}_{\mathbf{deformed}})& =\mathbf{F}({\mathbf{b}}_{\mathbf{rest}}-{\mathbf{c}}_{\mathbf{rest}})\end{array}$$

现在 ${\mathbf{F}}_{2\times 2}$ 有四个线性约束：

$$\{\begin{array}{ll}\mathbf{B}& =[{\mathbf{b}}_{\mathbf{rest}}-{\mathbf{a}}_{\mathbf{rest}}|{\mathbf{c}}_{\mathbf{rest}}-{\mathbf{a}}_{\mathbf{rest}}{]}^{-1}\\ \mathbf{D}& =[{\mathbf{b}}_{\mathbf{deformed}}-{\mathbf{a}}_{\mathbf{deformed}}|{\mathbf{c}}_{\mathbf{deformed}}-{\mathbf{a}}_{\mathbf{deformed}}]\\ \mathbf{F}& =\mathbf{DB}=[{\overrightarrow{ab}}_{\mathbf{deformed}}|{\overrightarrow{ac}}_{\mathbf{deformed}}][{\overrightarrow{ab}}_{\mathbf{rest}}|{\overrightarrow{ac}}_{\mathbf{rest}}{]}^{-1}\end{array}$$

B = ti.Matrix(dim, dim, dt=real, shape=n_elements)
elements = ti.var(dt=ti.i32, shape=(n_elements, 3))

@ti.func
def compute_D(i):
    a = elements[i, 0]
    b = elements[i, 1]
    c = elements[i, 2]
    return ti.Matrix.cols([pars[b] - pars[a], pars[c] - pars[a]])

@ti.kernel
def compute_B():
    for i in range(n_elements):
        B[i] = compute_D(i).inverse()

@ti.kernel
def compute_total_energy():
    for i in range(n_elements):
        D = compute_D(i)
        F = D @ B[i]

        # Neo Hookean ：见 3.1
        ......

同理，对于三维，有：

$$\{\begin{array}{ll}\mathbf{B}& =[{\mathbf{b}}_{\mathbf{rest}}-{\mathbf{a}}_{\mathbf{rest}}|{\mathbf{c}}_{\mathbf{rest}}-{\mathbf{a}}_{\mathbf{rest}}|{\mathbf{d}}_{\mathbf{rest}}-{\mathbf{a}}_{\mathbf{rest}}{]}^{-1}\\ \mathbf{D}& =[{\mathbf{b}}_{\mathbf{deformed}}-{\mathbf{a}}_{\mathbf{deformed}}|{\mathbf{c}}_{\mathbf{deformed}}-{\mathbf{a}}_{\mathbf{deformed}}|{\mathbf{d}}_{\mathbf{deformed}}-{\mathbf{a}}_{\mathbf{deformed}}]\\ \mathbf{F}& =\mathbf{DB}=[{\overrightarrow{ab}}_{\mathbf{deformed}}|{\overrightarrow{ac}}_{\mathbf{deformed}}|{\overrightarrow{ad}}_{\mathbf{deformed}}][{\overrightarrow{ab}}_{\mathbf{rest}}|{\overrightarrow{ac}}_{\mathbf{rest}}|{\overrightarrow{ad}}_{\mathbf{rest}}{]}^{-1}\end{array}$$

@ti.func
def compute_D(i):
    a = elements[i, 0]
    b = elements[i, 1]
    c = elements[i, 2]
    d = elements[i, 3]
    return ti.Matrix.cols([pars[b] - pars[a], pars[c] - pars[a], pars[d] - pars[a]])


@ti.kernel
def compute_B():
    for i in range(n_elements):
        B[i] = compute_D(i).inverse()


@ti.kernel
def compute_total_energy():
    for i in range(n_elements):
        D = compute_D(i)
        F = D @ B[i]

        # Neo Hookean ：见 3.1
        ......

Note ：

• 其中 $\mathbf{B}$ 在整个物理过程中是常数。因此可进行预计算；
• 对于二维微元（三角形），用两条向量 $\overrightarrow{ab}$ 和 $\overrightarrow{ac}$ 来作为基，通过张成对应的列空间的变换，来表示形变；
• 对于三维微元（四面体），用三条向量 $\overrightarrow{ab}$ 、 $\overrightarrow{ac}$ 和 $\overrightarrow{ad}$ 来作为基，通过张成对应的列空间的变换，来表示形变。

4.4 显式时间积分

$$\begin{array}{rl}{\mathbf{v}}_{t+1,i}& ={\mathbf{v}}_{t,i}+\Delta t\frac{{\mathbf{f}}_{t,i}}{m_i}\\ {\mathbf{x}}_{t+1,i}& ={\mathbf{x}}_{t,i}+\Delta t{\mathbf{v}}_{t+1,i}\end{array}$$

• ${\mathbf{v}}_{t,i}$ 和 ${\mathbf{x}}_{t,i}$ 存储在顶点中。

弹性势能对位置求导，结果的相反值即为顶点的受力：

$$\begin{array}{rl}{\mathbf{f}}_{t,i}& =-\frac{\partial U}{\partial {\mathbf{x}}_i}\\ & =-\sum _e\frac{\partial U(e)}{\partial {\mathbf{x}}_i}\\ & =-\sum _e{V}_e\frac{\partial \Psi ({\mathbf{F}}_e)}{\partial {\mathbf{F}}_e}\frac{\partial {\mathbf{F}}_e}{\partial {\mathbf{x}}_i}\\ & =-\sum _e{V}_e\mathbf{P}({\mathbf{F}}_e)\frac{\partial {\mathbf{F}}_e}{\partial {\mathbf{x}}_i}\end{array}$$

damping = 6

@ti.kernel
def integrate():
    for p in pars:
        ...... # 碰撞检测
        # 显式时间积分
        vels[p] = (vels[p] + ((-pars.grad[p] / node_mass) + ti.Vector([0, -10])) * dt) * math.exp(- damping * dt)
        pars[p] += dt * vels[p]

• 其中：

$${\mathbf{v}}_{t+1,i}=\left({\mathbf{v}}_{t,i}+\frac{{\mathbf{f}}_{t,i}+m_{i}g}{m_i}\Delta t\right)e^{-damping\Delta t}$$

4.5 隐式时间积分

TODO

4.6 自相交处理

• IPC: SIGGRAPH 2020开源有限元碰撞独家处理方案
• IPC 主页

4.7 运行结果

5. TetGen

5.1 下载链接

5.1.1 TetGen下载

http://wias-berlin.de/software/index.jsp?id=TetGen&lang=1

5.1.2 TetView 下载

http://wias-berlin.de/software/tetgen/tetview.html

5.2 环境配置

5.2.1 源码编译

使用 CMAKE 编译源码，获得 tetgen.exe 文件：

5.2.2 环境变量

将 tetgen.exe 文件所在目录添加到 系统变量 中的 PATH ，同时可将下载的 tetview.exe 文件也一同放入该目录下。

5.2.3 检测路径

用管理员模式打开 powershell ，输入以下命令：

tetgen -h

显示帮助提示，则安装成功：

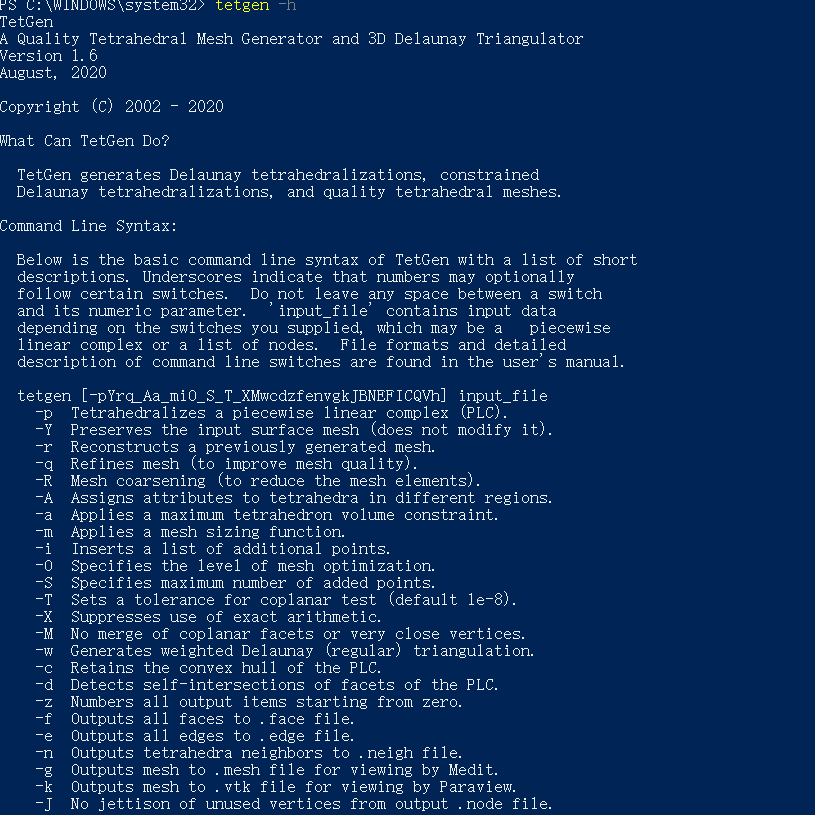
5.3.1 命令

-p  Tetrahedralizes a piecewise linear complex (PLC).
-Y  Preserves the input surface mesh (does not modify it).
-r  Reconstructs a previously generated mesh.
-q  Refines mesh (to improve mesh quality).
-R  Mesh coarsening (to reduce the mesh elements).
-A  Assigns attributes to tetrahedra in different regions.
-a  Applies a maximum tetrahedron volume constraint.
-m  Applies a mesh sizing function.
-i  Inserts a list of additional points.
-O  Specifies the level of mesh optimization.
-S  Specifies maximum number of added points.
-T  Sets a tolerance for coplanar test (default 1e-8).
-X  Suppresses use of exact arithmetic.
-M  No merge of coplanar facets or very close vertices.
-w  Generates weighted Delaunay (regular) triangulation.
-c  Retains the convex hull of the PLC.
-d  Detects self-intersections of facets of the PLC.
-z  Numbers all output items starting from zero.
-f  Outputs all faces to .face file.
-e  Outputs all edges to .edge file.
-n  Outputs tetrahedra neighbors to .neigh file.
-g  Outputs mesh to .mesh file for viewing by Medit.
-k  Outputs mesh to .vtk file for viewing by Paraview.
-J  No jettison of unused vertices from output .node file.
-B  Suppresses output of boundary information.
-N  Suppresses output of .node file.
-E  Suppresses output of .ele file.
-F  Suppresses output of .face and .edge file.
-I  Suppresses mesh iteration numbers.
-C  Checks the consistency of the final mesh.
-Q  Quiet:  No terminal output except errors.
-V  Verbose:  Detailed information, more terminal output.
-h  Help:  A brief instruction for using TetGen.

5.3.2 使用步骤

• 打开 PowerShell ，进入目标模型文件：

cd ......(路径)

• 使用命令调用 tetgen 或者 tetview ：

对 example.poly 进行四面体剖分：

tetgen –p example

可视化：

tetview example.poly
tetview example.ele

5.4 文件格式

详情见《TetGen用户手册》

5.4.1 .node 文件

第一行：<点个数> <维数(3)> <属性个数> <边界标识(0或者1)>

剩下的行为点列表：
<点编号> <x> <y> <z> [属性] [边界标识]

• 一个 .node 文件包括三维点列表，每个点有三维坐标(x,y,z)，或者有1个或者多个属性和边界标识；
• .node 文件可以作为输入或者输出文件以表示 PLC 点集，或者一个格网的点集，或者嵌入到格网中的附加点集(使用 -i 参数)；
• 属性为与点关联的浮点型物理量值(例如：质量、导电性等)，并不加修改的复制到格网
  中
  • 如果 -p ， -q ， -a 或者 -i 是选择的，每个 Steiner 点添加到格网中默认属性值为 0 ；
  • 如果指明了 -w (权重 Delaunay 四面体剖分)项，第一个属性为相应点的权重；
  • 如果第一行的第四部分值为1，文件中最后一列为边界标识。边界标识用于识别边界点(点在PLC面上)，除了 TetGen 禁用了 -B 了开关，否则 TetGen 生成的 .node 文件包含边界标识。

文件示例 ：

# 节点格式, 3 维, 没有属性, 没有边界标识
8 3 0 0
# 节点编号, 节点坐标
1 0.0 0.0 0.0
2 1.0 0.0 0.0
3 1.0 1.0 0.0
4 0.0 1.0 0.0
5 0.0 0.0 1.0
6 1.0 0.0 1.0
7 1.0 1.0 1.0
8 0.0 1.0 1.0

python 读取示例 ：

self.node_data = []

# read nodes from *.node file
with open(filename+".node", "r") as node_file:
    node_line = int(node_file.readline().split()[0])
    for i in range(node_line):
        self.node_data += [float(x) for x in node_file.readline().split()[1:4]] #[x, y, z]

self.node_num = int(len(self.node_data)/3)
self.pars = ti.Vector(self.dim, dt=ti.f32, shape=self.node_num)

for i in range(self.node_num):
    self.pars[i] = [self.node_data[3*i], self.node_data[3*i+1], self.node_data[3*i+2]]
    self.vels[i] = [0, 0, 0]

包围盒：

self.center = ti.Vector(self.dim, ti.f32, shape=())
self.lowerCorner = ti.Vector(self.dim, ti.f32, shape=())
self.higherCorner = ti.Vector(self.dim, ti.f32, shape=())


for i in range(self.node_num):
    self.center[None].x += self.pars[i].x
    self.center[None].y += self.pars[i].y
    self.center[None].z += self.pars[i].z
    self.lowerCorner[None].x = min(self.lowerCorner[None].x, self.pars[i].x)
    self.lowerCorner[None].y = min(self.lowerCorner[None].y, self.pars[i].y)
    self.lowerCorner[None].z = min(self.lowerCorner[None].z, self.pars[i].z)
    self.higherCorner[None].x = max(self.higherCorner[None].x, self.pars[i].x)
    self.higherCorner[None].y = max(self.higherCorner[None].y, self.pars[i].y)
    self.higherCorner[None].z = max(self.higherCorner[None].z, self.pars[i].z)

self.center[None].x /= max(self.node_num, 1)
self.center[None].y /= max(self.node_num, 1)
self.center[None].z /= max(self.node_num, 1)

open 参数
“+”	表示拥有读和写功能
“r”	表示只读
“r+”	表示可读可写，不能创建文件
“w”	表示可写
“w+”	表示可读可写，文件不存在则创建，存在则覆盖原先内容，原则就是创建一个新文件
“a”	可写
“a+”	表示可读可写，文件不存在则创建，追加内容在原本数据的末尾

5.4.2 .face 文件

First line: <# of faces> <boundary marker (0 or 1)>

Remaining lines list # of faces:
<face #> <node> <node> <node> ... [boundary marker] ...

• 基本的形式为每个三角面有三个角点,或者包含一个边界标识；
• 记录与 .node 文件中相关联的编号。

文件示例 ：

# 面个数 边界标识
12  0
# 面编号 顶点1 顶点2 顶点3
    1      1     2     3
    2      6     5     7
    3      3     4     1
    4      6     2     1
    5      7     5     8
    6      3     2     7
    7      1     5     6
    8      8     4     3
    9      7     2     6
   10      8     5     1
   11      7     8     3
   12      1     4     8

python 读取示例 ：

self.face_data = []

# read faces from *.face file (only for rendering)
with open(filename+".face", "r") as face_file:
    face_line = int(face_file.readline().split()[0])
    for i in range(face_line):
        self.face_data += [int(ind)-index_start for ind in face_file.readline().split()[1:4]] # triangle

self.face_num = int(len(self.face_data)/3)
self.faces = ti.Vector(3, dt=ti.i32, shape=self.face_num)

for i in range(self.face_num):
    self.faces[i] = [self.face_data[3*i], self.face_data[3*i+1], self.face_data[3*i+2]]

5.4.3 .ele 文件

First line: <# of tetrahedra> <nodes per tet. (4 or 10)> <region attribute (0 or 1)>

Remaining lines list # of tetrahedra:
<tetrahedron #> <node> <node> ... <node> [attribute]
...

• .ele 文件保存了四面体列表；
• 每个四面体有四个角点（如果使用了 -o2 命令将有 10 个角点）；
• 记录了对应与 .node 文件的顶点索引号，开始的四个节点为角点顶点；
• 如果开启了 -o2 那么余下的六个节点为四面体边界的中间点。

文件示例 ：

# 元素数 每个元素的顶点数
6  4  0
# 元素编号 顶点1 顶点2 顶点3 顶点4
    1       6     7     1     5
    2       1     8     3     4
    3       3     7     1     2
    4       1     7     6     2
    5       1     7     3     8
    6       7     8     1     5

python 读取示例 ：

self.elem_data = []

# read elements from *.ele file
with open(filename+".ele", "r") as elem_file:
    elem_line = int(elem_file.readline().split()[0])
    for i in range(elem_line):
        self.elem_data += [ int(ind)-index_start for ind in elem_file.readline().split()[1:5] ] # tetrahedron

self.elem_num = int(len(self.elems)/4)
self.elements = ti.Vector(4, dt=ti.i32, shape=self.elem_num)

for i in range(self.elem_num):
    self.elements[i] = [self.elem_data[4*i], self.elem_data[4*i+1], self.elem_data[4*i+2], self.elem_data[4*i+3]]