
定义
树状数组或二叉索引树(英语:Binary Indexed Tree),又以其发明者命名为Fenwick树,最早由Peter M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和, 区间和。
原码,反码,补码的产生过程,就是为了解决,计算机做减法和引入符号位(正号和负号)的问题。
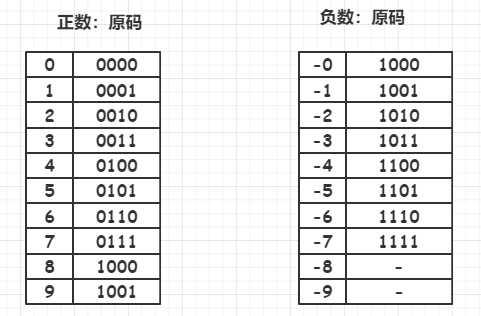
原码
是最简单的机器数表示法。用最高位表示符号位,‘1’表示负号,‘0’表示正号。其他位存放该数的二进制的绝对值。
若以带符号位的四位二进值数为例
1010: 最高位为1,表示这是一个负数,其他三位为010即(0*2^2)+(1*2^1)+(0*2^0)=2(‘^’表示幂运算符)所以1010表示十进制数(-2)。
反码
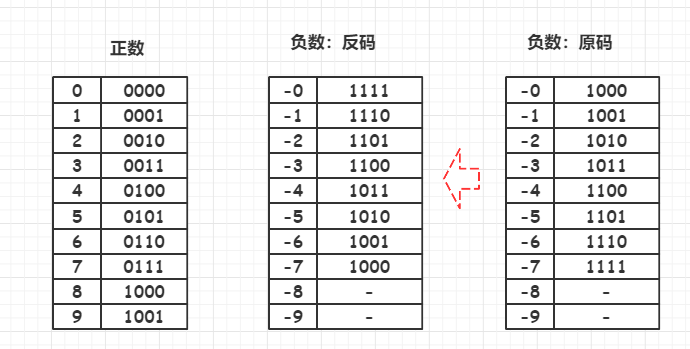
正数的反码还是等于原码,负数的反码就是他的原码除符号位外,按位取反
若以带符号位的四位二进制数为例:
3是正数,反码与原码相同,则可以表示为0011-3的原码是1011,符号位保持不变,低三位(011)按位取反得(100)所以-3的反码为1100
补码
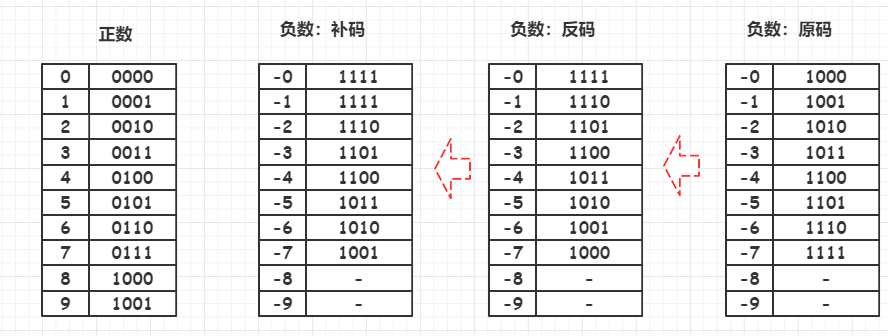
正数的补码等于他的原码,负数的补码等于反码+1。(这只是一种算补码的方式,多数书对于补码就是这句话
负数的补码等于他的原码自低位向高位,尾数的第一个‘1’及其右边的‘0’保持不变,左边的各位按位取反,符号位不变。
树状数组
C
[
1
]
=
A
[
1
]
C[1] = A[1]
C[1]=A[1]
C
[
2
]
=
A
[
1
]
+
A
[
2
]
C[2] = A[1] + A[2]
C[2]=A[1]+A[2]
C
[
3
]
=
A
[
3
]
C[3] = A[3]
C[3]=A[3]
C
[
4
]
=
A
[
1
]
+
A
[
2
]
+
A
[
3
]
+
A
[
4
]
C[4] = A[1] + A[2] + A[3] + A[4]
C[4]=A[1]+A[2]+A[3]+A[4]
C
[
5
]
=
A
[
5
]
C[5] = A[5]
C[5]=A[5]
C
[
6
]
=
A
[
5
]
+
A
[
6
]
C[6] = A[5] + A[6]
C[6]=A[5]+A[6]
C
[
7
]
=
A
[
7
]
C[7] = A[7]
C[7]=A[7]
C
[
8
]
=
A
[
1
]
+
A
[
2
]
+
A
[
3
]
+
A
[
4
]
+
A
[
5
]
+
A
[
6
]
+
A
[
7
]
+
A
[
8
]
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]
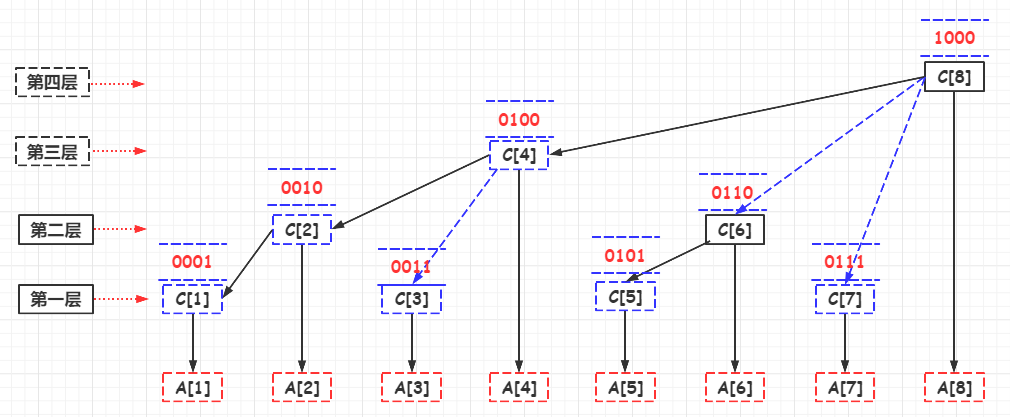
C [ i ] = A [ i − 2 k + 1 ] + A [ i − 2 k + 2 ] + . . . + A [ i ] C[i]=A[i−2^k+1]+A[i−2^k+2]+...+A[i] C[i]=A[i−2k+1]+A[i−2k+2]+...+A[i]
其中k为i的二进制中最低位到最高位连续0的长度,
1.举例 ,6,二进制为0110, 这时候k为1,从右往左数0,遇到第一个1的时候停下来:
C [ 6 ] = A [ 6 − 2 1 + 1 ] + A [ 6 ] C[6]=A[6−2^1+1]+A[6] C[6]=A[6−21+1]+A[6] => C [ 6 ] = A [ 5 ] + A [ 6 ] C[6]=A[5]+A[6] C[6]=A[5]+A[6]
可能有疑问指出,为什么不是
C [ 6 ] = A [ 6 − 2 1 + 1 ] + A [ 6 − 2 1 + 2 ] + . . . + A [ 6 ] C[6]=A[6−2^1+1]+A[6−2^1+2]+...+A[6] C[6]=A[6−21+1]+A[6−21+2]+...+A[6] => C [ 6 ] = A [ 5 ] + A [ 6 ] + . . . + A [ i ] C[6]=A[5]+A[6]+...+A[i] C[6]=A[5]+A[6]+...+A[i]
因为6的二进制为0110,其低位只有10,也就是两个元素,即 C [ 6 ] C[6] C[6]只管理两个节点,对应图上可以看出是 A [ 6 ] A[6] A[6]与 A [ 5 ] A[5] A[5]
2.举例,4 二进制为0100,这时候k为2,从右往左数,遇到第一个1的时候停下来:
C [ 4 ] = A [ i − 2 2 + 1 ] + A [ i − 2 2 + 2 ] + . . . + A [ i ] C[4]=A[i−2^2+1]+A[i−2^2+2]+...+A[i] C[4]=A[i−22+1]+A[i−22+2]+...+A[i] => C [ 4 ] = A [ 1 ] + A [ 2 ] + A [ 3 ] + A [ 4 ] C[4]=A[1]+A[2]+A[3]+A[4] C[4]=A[1]+A[2]+A[3]+A[4]
找前7项的和
S U M = C [ 7 ] + C [ 7 − 2 k 1 ] + C [ ( 7 − 2 k 1 ) − 2 k 2 ] SUM=C[7]+C[7-2^{k1}]+C[(7-2^{k1})-2^{k2}] SUM=C[7]+C[7−2k1]+C[(7−2k1)−2k2] => S U M = C [ 7 ] + C [ 7 − 2 0 ] + C [ ( 7 − 2 0 ) − 2 1 ] SUM=C[7]+C[7-2^0]+C[(7-2^0)-2^1] SUM=C[7]+C[7−20]+C[(7−20)−21] => S U M = C [ 7 ] + C [ 6 ] + C [ 4 ] SUM=C[7]+C[6]+C[4] SUM=C[7]+C[6]+C[4]
k
1
k1
k1 为7的二进制中从最低位到高位连续零的长度
k
2
k2
k2 为6的二进制中从最低位到高位连续零的长度
k
3
k3
k3 为4的二进制中从最低位到高位连续零的长度
公式:
S U M = C [ i ] + C [ i − 2 k 1 ] + C [ ( i − 2 k 1 ) − 2 k 2 ] + . . . SUM=C[i]+C[i-2^{k1}]+C[(i-2^{k1})-2^{k2}]+... SUM=C[i]+C[i−2k1]+C[(i−2k1)−2k2]+...
l o w b i t ( x ) lowbit(x) lowbit(x)= KaTeX parse error: Expected 'EOF', got '&' at position 2: x&̲(-x)
- 当x为0时结果为0
- x为奇数时,结果为1
- x为偶数时,结果为x中2的最大次方的因子,即 2 k 2^k 2k
离散化
针对数值的大小做一个排名的「映射」,把原始数据映射到 [1, len] 这个区间,这样「树状数组」底层的数组空间会更紧凑,更易于维护。
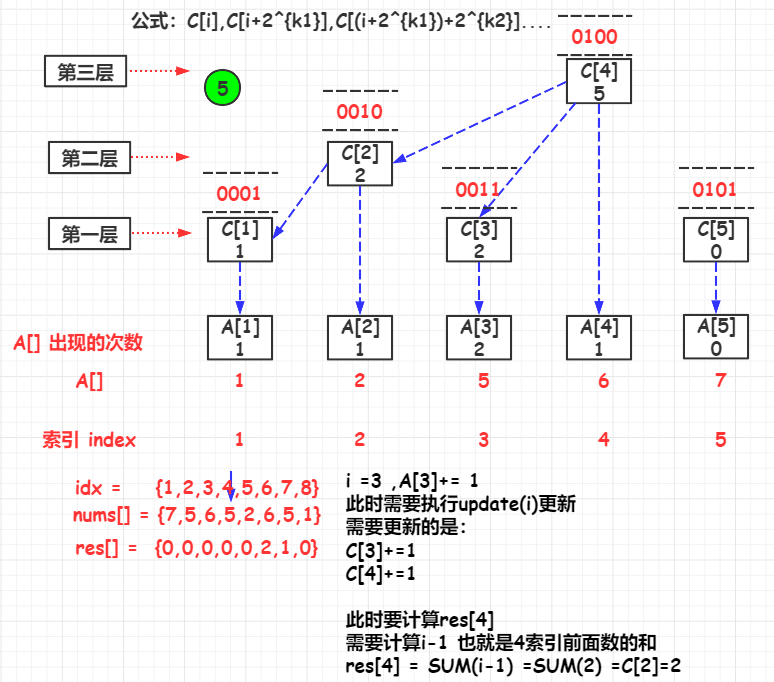
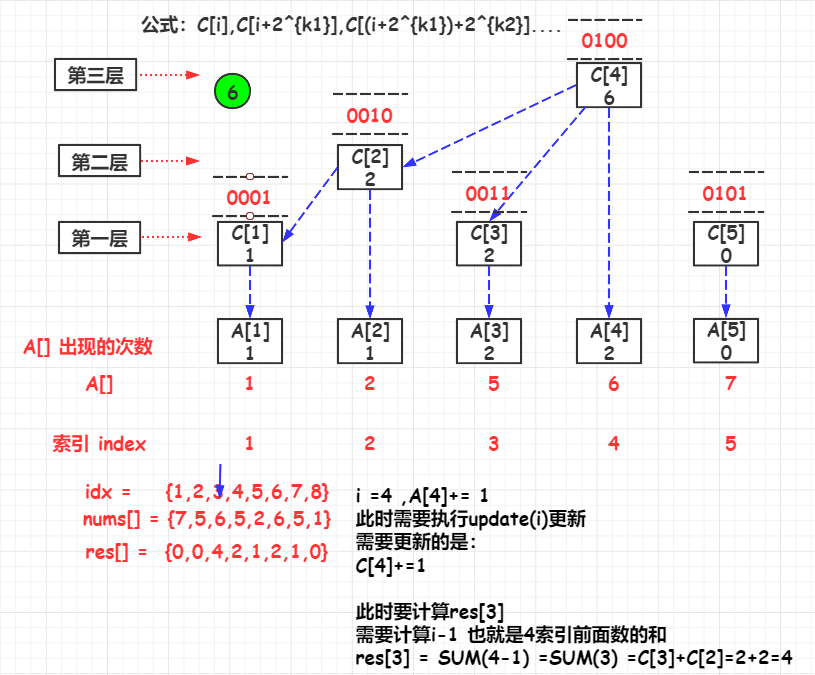
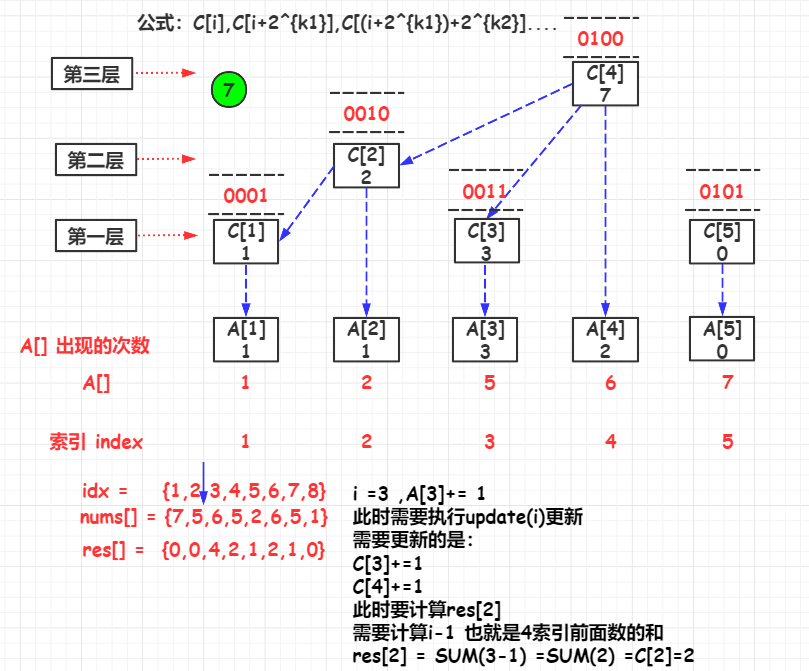
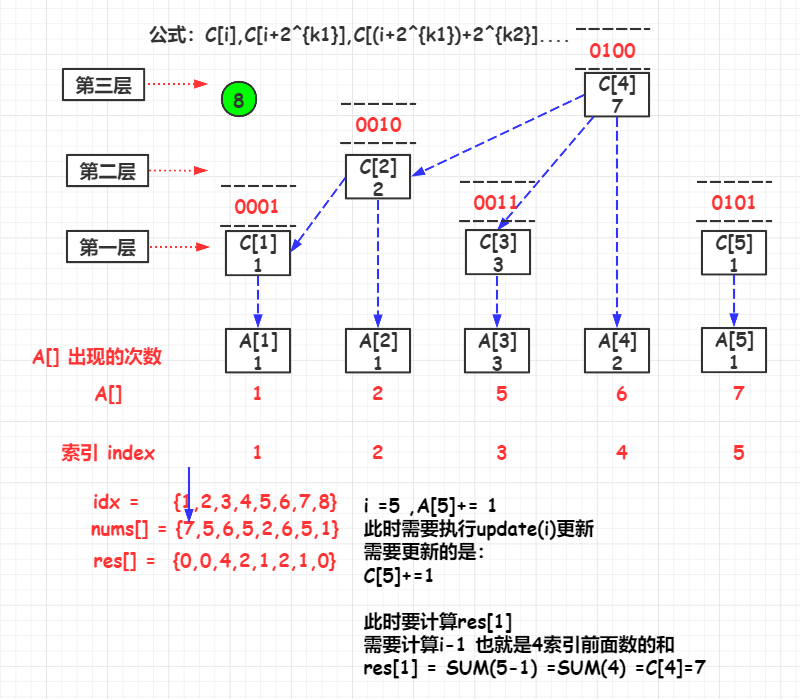
update(i)
如果要更新 A [ i ] A[i] A[i]的值时,与 A [ i ] A[i] A[i]直接关联的 C [ ] C[] C[]有:
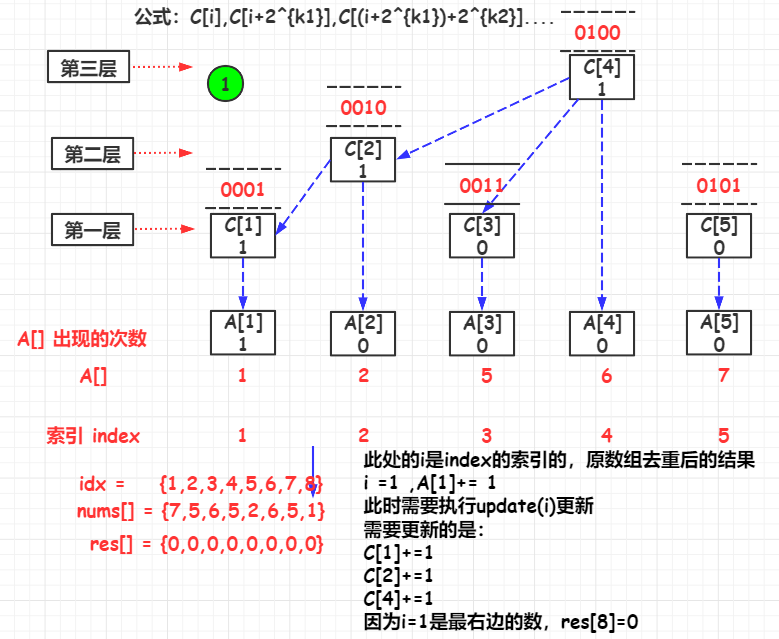
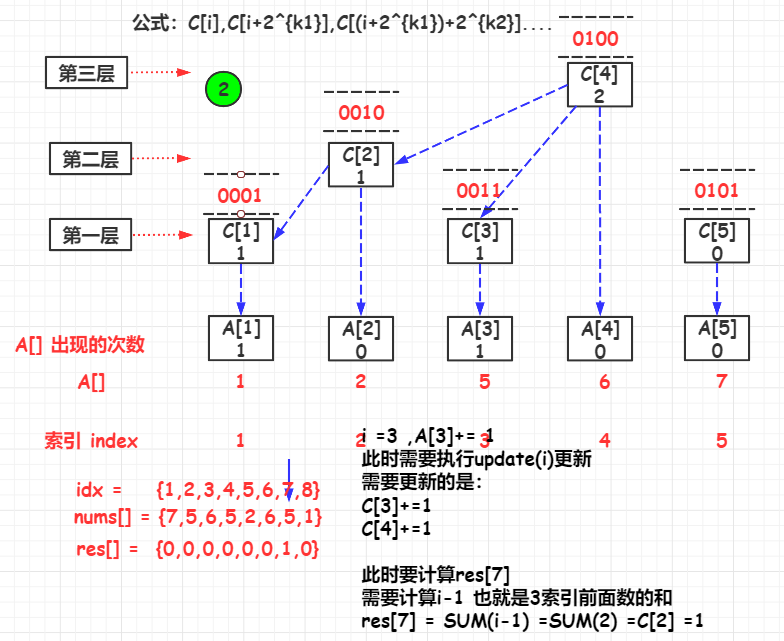
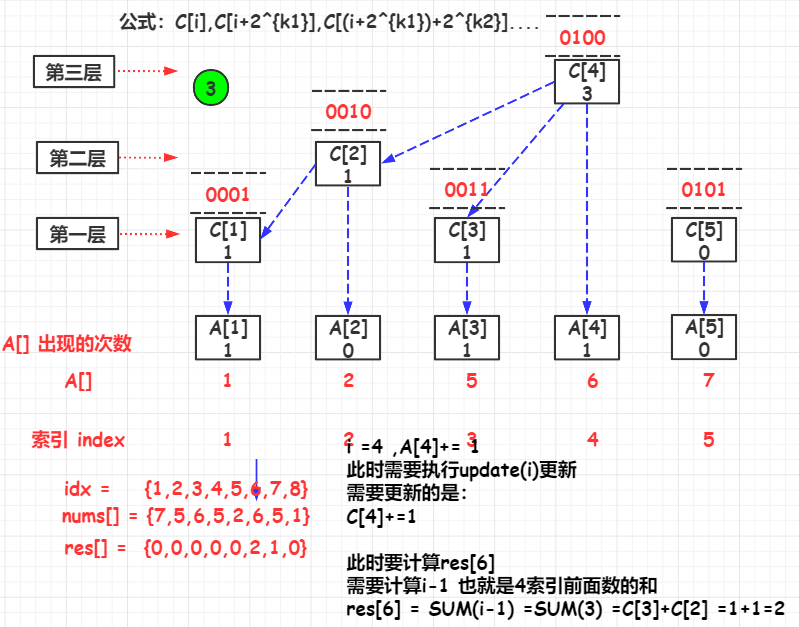
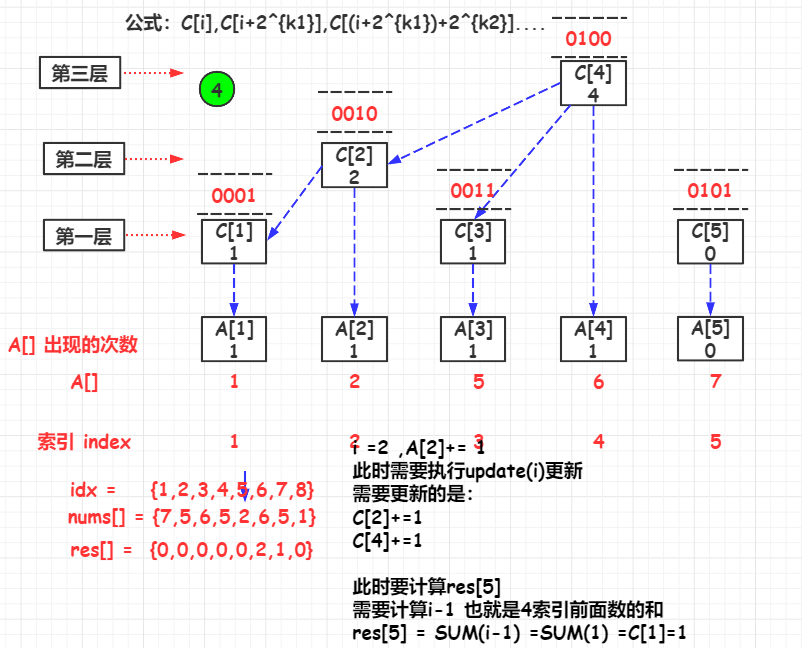
C [ i ] , C [ i + 2 k 1 ] , C [ ( i + 2 k 1 ) + 2 k 2 ] . . . . C[i],C[i+2^{k1}],C[(i+2^{k1})+2^{k2}].... C[i],C[i+2k1],C[(i+2k1)+2k2]....
其中, i i i是初始索引, k 1 k1 k1是 i i i的 l o w b i t lowbit lowbit, k 2 k2 k2是 i − 2 k 1 i-2{k1} i−2k1的 l o w b i t lowbit lowbit
举例: A [ 1 ] A[1] A[1],与其直接关联的 C [ ] C[] C[]有:
C [ i ] , C [ i + 2 k 1 ] , C [ ( i + 2 k 1 ) + 2 k 2 ] . . . . C[i],C[i+2^{k1}],C[(i+2^{k1})+2^{k2}].... C[i],C[i+2k1],C[(i+2k1)+2k2].... => C [ 1 ] , C [ 1 + 2 1 ] , C [ ( i + 2 1 ) + 2 2 ] . . . . C[1],C[1+2^1],C[(i+2^1)+2^2].... C[1],C[1+21],C[(i+21)+22].... => C [ 1 ] , C [ 2 ] , C [ 4 ] C[1],C[2],C[4] C[1],C[2],C[4]
其代码实现是实现
l
o
w
b
i
t
lowbit
lowbit的增加,i += lowbit(i) 但是i的值不能超过n
query(i)
其代码实现是实现
l
o
w
b
i
t
lowbit
lowbit的减少,i -= lowbit(i),但是i的值不能小于1
举例,参考的yangbingjie的题解的例子
FenwickTree
class FenwickTree {
int n;
int[] C;
//初始化
public FenwickTree(int n) {
this.n = n;
this.C = new int[n];
}
// 单点更新:将 i 位置与其直接关联的 C 都更新一遍
public void update(int i) {
while (i < n) {
C[i]++;
i += lowbit(i);
}
}
//传进来的值-1过,查询之前有多少个数
//区间查询:查询小于等于 i 的元素个数
public int query(int i) {
int sum = 0;
while (i >= 1) {
sum += C[i];
i -= lowbit(i);
}
return sum;
}
//算lowbit
public int lowbit(int x) {
return x & (-x);
}
}
主体代码
思路
- 预处理
n
u
m
s
nums
nums数组,使用
TreeSet的结构去重排序 - 做一个 M a p < k , v > Map<k,v> Map<k,v>其中 k k k是 n u m s nums nums中的数字, v v v是改元素的排名,从小到大排列
- 初始化 F e n w i c k T r e e FenwickTree FenwickTree,多放一个位置,使下标从1开始
- 从右到左遍历,获取到该元素的排名后(离散化后索引),
public List<Integer> countSmaller(int[] nums) {
List<Integer> res = new ArrayList<>();
int len = nums.length;
if (len == 0) return res;
//1.预处理nums
Set<Integer> treeSet = new TreeSet<>();
for (int num : nums) treeSet.add(num);
//2.匹配映射关系的map
Map<Integer, Integer> map = new HashMap<>();
int rank = 1;//相当于A数组的下标索引
for (int num : treeSet) {
map.put(num, rank++);
}
//3.初始化FenwickTree
FenwickTree fenwickTree = new FenwickTree(treeSet.size() + 1);
for (int i = nums.length - 1; i >= 0; i--) {
rank = map.get(nums[i]);
//更新当前的元素的C[rank]
fenwickTree.update(rank);
//当前排名前的元素的个数
res.add(fenwickTree.query(rank - 1));
}
Collections.reverse(res);
return res;
}
}
























 380
380











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








