激活函数与损失函数及其常见问题

一、激活函数 Sigmoid、tanh、ReLU、LeakyReLU、PReLU、RReLU

0.激活函数的作用

• 神经网络为什么需要激活函数：首先数据的分布绝大多数是非线性的，而一般神经网络的计算是线性的，引入激活函数，是在神经网络中引入非线性，强化网络的学习能力。所以激活函数的最大特点就是非线性。
• 不同的激活函数，根据其特点，应用也不同。Sigmoid和tanh的特点是将输出限制在(0,1)和(-1,1)之间，说明Sigmoid和tanh适合做概率值的处理，例如LSTM中的各种门；而ReLU就不行，因为ReLU无最大值限制，可能会出现很大值。同样，根据ReLU的特征，Relu适合用于深层网络的训练，而Sigmoid和tanh则不行，因为它们会出现梯度消失。
• 在使用relu的网络中，是否还存在梯度消失的问题？梯度衰减因子包括激活函数导数，此外，还有多个权重连乘也会影响。。。梯度消失只是表面说法，按照这样理解，底层使用非常大的学习率，或者人工添加梯度噪音，原则上也能回避，有不少论文这样试了，然而目前来看，有用，但没太大的用处。深层原因训练不好的本质难题可能不是衰减或者消失（残差网络论文也提到这一点），是啥目前数理派也搞不清楚，所以写了论文也顺势这样说开了。不然，贸贸然将开山鼻祖的观点否定了，是需要极大勇气和大量的实验，以及中二精神的。

1.sigmoid

sigmod函数的取值范围在（0, 1）之间，可以将网络的输出映射在这一范围，方便分析。

Sigmoid公式及导数：

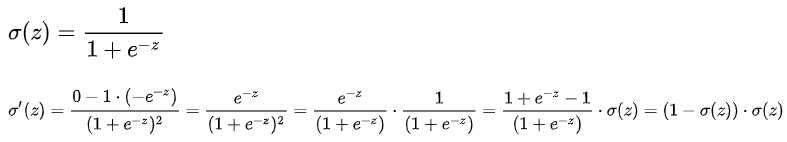
Sigmoid作为激活函数的特点：

优点：平滑、易于求导。

缺点：

• 激活函数计算量大（在正向传播和反向传播中都包含幂运算和除法）；
• 反向传播求误差梯度时，求导涉及除法；
• Sigmoid导数取值范围是[0, 0.25]，由于神经网络反向传播时的“链式反应”，很容易就会出现梯度消失的情况。例如对于一个10层的网络， 根据$0.25^{10}\approx 0.000000954$，第10层的误差相对第一层卷积的参数$W_1$的梯度将是一个非常小的值，这就是所谓的“梯度消失”。
• Sigmoid的输出不是0均值（即zero-centered）；这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入，随着网络的加深，会改变数据的原始分布。

2.tanh

双曲正切函数，其英文读作Hyperbolic Tangent。tanh和 sigmoid 相似，都属于饱和激活函数，区别在于输出值范围由 (0,1) 变为了 (-1,1)，可以把 tanh 函数看做是 sigmoid 向下平移和拉伸后的结果。

tanh公式及导数：
$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{2}{1+e^{-2x}}-1$

$tan{h}^{\prime }(x)=1-\frac{(e^x-e^{-x}{)}^2}{(e^x+e^{-x}{)}^2}=1-tan{h}^2(x)$

tanh作为激活函数的特点：

相比Sigmoid函数，

• tanh的输出范围时(-1, 1)，解决了Sigmoid函数的不是zero-centered输出问题；
• 幂运算的问题仍然存在；
• tanh导数范围在(0, 1)之间，相比sigmoid的(0, 0.25)，梯度消失（gradient vanishing）问题会得到缓解，但仍然还会存在。

3.ReLU

Relu(Rectified Linear Unit)——修正线性单元函数：该函数形式比较简单.
公式：$relu=max(0,x)$

从上图可知，ReLU的有效导数是常数1，解决了深层网络中出现的梯度消失问题，也就使得深层网络可训练。同时ReLU又是非线性函数，所谓非线性，就是一阶导数不为常数；对ReLU求导，在输入值分别为正和为负的情况下，导数是不同的，即ReLU的导数不是常数，所以ReLU是非线性的（只是不同于Sigmoid和tanh，relu的非线性不是光滑的）

ReLU在x>0下，导数为常数1的特点：
导数为常数1的好处就是在“链式反应”中不会出现梯度消失，但梯度下降的强度就完全取决于权值的乘积，这样就可能会出现梯度爆炸问题。解决这类问题：一是控制权值，让它们在（0，1）范围内；二是做梯度裁剪，控制梯度下降强度，如$ReLU(x)=min(6,max(0,x))$

ReLU在x<0下，输出置为0的特点：
描述该特征前，需要明确深度学习的目标：深度学习是根据大批量样本数据，从错综复杂的数据关系中，找到关键信息（关键特征）。换句话说，就是把密集矩阵转化为稀疏矩阵，保留数据的关键信息，去除噪音，这样的模型就有了鲁棒性。ReLU将x<0的输出置为0，就是一个去噪音，稀疏矩阵的过程。而且在训练过程中，这种稀疏性是动态调节的，网络会自动调整稀疏比例，保证矩阵有最优的有效特征。
但是ReLU 强制将x<0部分的输出置为0（置为0就是屏蔽该特征），可能会导致模型无法学习到有效特征，所以如果学习率设置的太大，就可能会导致网络的大部分神经元处于‘dead’状态，所以使用ReLU的网络，学习率不能设置太大。

ReLU作为激活函数的特点：

• 相比Sigmoid和tanh，ReLU摒弃了复杂的计算，提高了运算速度。
• 解决了梯度消失问题，收敛速度快于Sigmoid和tanh函数，但要防范ReLU的梯度爆炸
• 容易得到更好的模型，但也要防止训练中出现模型‘Dead’情况。

4.Leaky ReLU, PReLU（Parametric Relu）, RReLU（Random ReLU）

为了防止模型的‘Dead’情况，后人将x<0部分并没有直接置为0，而是给了一个很小的负数梯度值$\alpha$。

Leaky ReLU中的$\alpha$为常数，一般设置 0.01。这个函数通常比 Relu 激活函数效果要好，但是效果不是很稳定，所以在实际中 Leaky ReLu 使用的并不多。

PRelu（参数化修正线性单元） 中的$\alpha$作为一个可学习的参数，会在训练的过程中进行更新。

RReLU（随机纠正线性单元）也是Leaky ReLU的一个变体。在RReLU中，负值的斜率在训练中是随机的，在之后的测试中就变成了固定的了。RReLU的亮点在于，在训练环节中，aji是从一个均匀的分布U(I,u)中随机抽取的数值($a_{ji}\sim U(l,u),l<uandl,u\in [0,1)$)。

5.ELU

ELU函数是针对ReLU函数的一个改进型，相比于ReLU函数，在输入为负数的情况下，是有一定的输出的，而且这部分输出还具有一定的抗干扰能力。这样可以消除ReLU死掉的问题，不过还是有梯度饱和和指数运算的问题。

函数公式：

$$f(x)=\{\begin{array}{rlr}& x& x>0\\ & \alpha (e^x-1)& x\le 0\end{array}$$

6.SELU

函数公式：
$$\lambda f(x)=\{\begin{array}{rlr}& x& x>0\\ & \alpha (e^x-1)& x\le 0\end{array}$$
它的值有正有负：在整个ReLU的family里里面，除了一开始最原始的ReLU以外都有负值，所以这个特性还好；
有 Saturation Region：其他的ReLU他们没有Saturation Region，但是他有Saturation Region，不过ELU其实也有Saturation Region，因为SELU就只是ELU乘上一个$\lambda$而已;乘上这个有什么不同？乘上$\lambda$，让它在某些区域的斜率是大于1的，意味着说你进来一个比较小的变化，通过Region以后，他把你的变化放大1.0507700987倍，所以它的input能是会被放大的，而且这是他一个ELU的没有的特色。

二、损失函数

0. 损失函数的作用

损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型的性能越好。不同的模型用的损失函数一般也不一样。

损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是指经验风险损失函数加上正则项。

1. 0-1损失函数（zero-one loss）

0-1损失是指预测值和目标值不相等时，损失函数值为1， 否则为0：
$$L(Y,f(X))=\{\begin{array}{rlr}& 1,& Y\ne f(X)\\ & 0,& Y=f(X)\end{array}$$
特点：

• 0-1损失函数直接对应分类判断错误的个数，但是它是一个非凸函数，不太适用.

• 感知机就是用的这种损失函数。但是相等这个条件太过严格，因此可以放宽条件，即满足 [公式] 时认为相等：
  $$L(Y,f(X))=\{\begin{array}{rlr}& 1,& |Y-f(X)|\ge T\\ & 0,& |Y-f(X)|<T\end{array}$$

2. 绝对值损失函数（L1 loss）

绝对值损失函数是计算预测值与目标值的差的绝对值：
$L(Y,f(X))=|Y-f(X)|$
特点：

• 经常应用于回归问题
• 显著性预测、抠图问题上，L1取得的效果较为尖锐

3. 平方损失函数（L2 loss）

平方损失函数标准形式如下：
$L(Y,f(X))={\sum }_N(Y-f(X){)}^2$
特点：

• 经常应用于回归问题
• • 显著性预测、抠图问题上，L2取得的效果较为平滑

4. log对数损失函数

log对数损失函数的标准形式如下：
$L(Y|P(Y|X))=-log(P(Y|X))$

特点：

• log对数损失函数能非常好的表征概率分布，在很多场景尤其是多分类，如果需要知道结果属于每个类别的置信度，那它非常适合。
• 健壮性不强，相比于hinge loss对噪声更敏感。
• 逻辑回归的损失函数就是log对数损失函数。

5. 指数损失函数（exponential loss）

指数损失函数的标准形式如下：
$L(Y|f(x))=exp(-Yf(X))$

在AdaBoost算法中，第m次迭代后，$f_m(x)$的值为：
$f_m(x)=f_{m-1}(x)+{\alpha }_m{G}_m(x)$

Adaboost每次迭代时的目的是为了找到最小化下列式子时的参数$\alpha$和$G$：
$argmi{n}_{\alpha ,G}={\sum }_{i=1}^{N}exp(-y_i(f_{m-1}(x)+{\alpha }_m{G}_m(x_i)))$

可以看出，Adaboost的目标式子就是指数损失，在给定N个样本的情况下，Adaboost的损失函数为：
$L(Y,f(X))=\frac{1}{N}{\sum }_{i=0}^{N}exp(-y_{i}f(x_i))$

特点：

• 对离群点、噪声非常敏感。经常用在AdaBoost算法中。

6. Hinge 损失函数

Hinge损失函数标准形式如下：
$L(Y,f(X))=max(0,1-Yf(X))$

特点：

• hinge损失函数表示如果被分类正确，损失为0，否则损失就为 [公式] 。SVM就是使用这个损失函数。
• 一般的$f(X)$ 是预测值，在-1到1之间，$Y$ 是目标值(-1或1)。其含义是，$f(X)$的值在-1和+1之间就可以了，并不鼓励$f(X>!)$ ，即并不鼓励分类器过度自信，让某个正确分类的样本距离分割线超过1并不会有任何奖励，从而使分类器可以更专注于整体的误差。
• 健壮性相对较高，对异常点、噪声不敏感，但它没太好的概率解释。

7. 感知损失函数 (perceptron loss)

感知损失函数的标准形式如下：
$L(Y,f(X))=max(0,-f(X))$

特点：

• 是Hinge损失函数的一个变种，Hinge loss对判定边界附近的点(正确端)惩罚力度很高。而perceptron loss只要样本的判定类别正确的话，它就满意，不管其判定边界的距离。它比Hinge loss简单，因为不是max-margin boundary，所以模型的泛化能力没 hinge loss强。

8. 交叉熵损失函数 (Cross-entropy loss function)

交叉熵损失函数的标准形式如下:

$L=\frac{1}{n}{\sum }_x(ylog(p(x))+(1-y)log(1-p(x)))$

其中$x$表示样本，$y$表示实际的标签，$p(x)$表示预测的输出，$n$ 表示样本总数量。

特点：

• 本质上也是一种对数似然函数，可用于二分类和多分类任务中。
  二分类问题中的loss函数（输入数据是softmax或者sigmoid函数的输出）：
  $L=\frac{1}{n}{\sum }_x(ylog(p(x))+(1-y)log(1-p(x)))$
  多分类问题中的loss函数（输入数据是softmax或者sigmoid函数的输出）：
  $L=\frac{1}{n}{\sum }_i{y}_{i}log(p(x_i))$

• 当使用sigmoid作为激活函数的时候，常用交叉熵损失函数而不用均方误差损失函数，因为它可以完美解决平方损失函数权重更新过慢的问题，具有“误差大的时候，权重更新快；误差小的时候，权重更新慢”的良好性质。

证明：

**交叉熵函数与最大似然函数的联系和区别**

结论：在分布符合伯努利分布的前提下，交叉熵损失函数与最大似然函数等价。
证明：