损失函数使用Relu或Logsigmoid的直观区别

        损失函数(loss function)或代价函数(cost function)是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数。在应用中，损失函数通常作为学习准则与优化问题相联系，即通过最小化损失函数求解和评估模型。例如在统计学和机器学习中被用于模型的参数估计(parametric estimation)，在宏观经济学中被用于风险管理(risk management)和决策 ，在控制理论中被应用于最优控制理论(optimal control theory)。

        Relu函数(百度)：线性整流函数（Linear rectification function），又称修正线性单元，是一种人工神经网络中常用的激活函数（activation function），通常指代以斜坡函数及其变种为代表的非线性函数。百度给出的定义：

        Logsigmoid函数(PyTorch文档)：

一、使用Relu时

        和实际上是一样的，但是在模型训练时，这两者是有所差别的，不过目前我没有太多的证据。其中一种损失函数是这样使用或的：

        如果我们只考虑前一项，且，即，那么它的函数图像如下：

二、使用Logsigmoid

        Logsigmoid在使用时需要加两个负号，其中一种损失函数(和上面对应，功能上差不多)是这样的：

        如果我们只考虑前一项，且，即，那么它的函数图像如下：

        在这里，我再详细地把的函数写出来吧，它是这样的：

        其中

        这样读者可以自行去研究这个函数图像。

三、两者比较

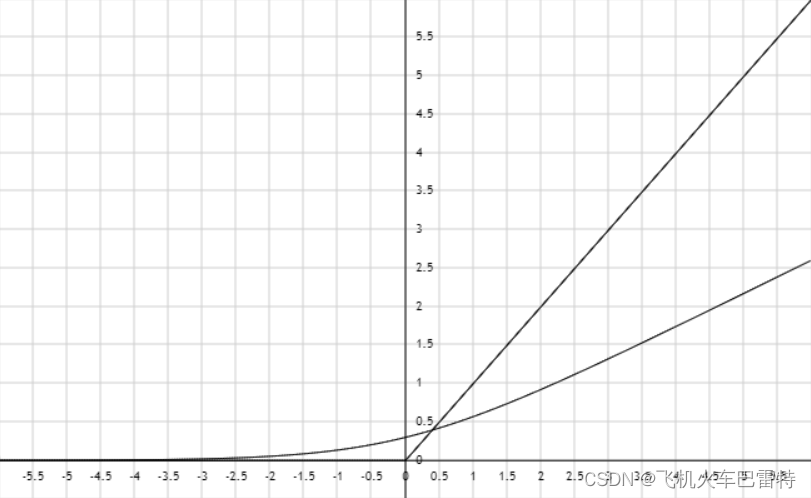
        将它们放在一起，我们能够得到下面的图像，可以发现它们确实很相似。不同的是，其中有一个很不平滑(Relu所起的作用)，而另一个很平滑(Logsigmoid所起的作用)。一般来说，Loss中使用平滑的Logsigmoid在性能上会比使用不平滑的Relu要更好。