Chapter 12: Continuous Latent Variables

一：Principal Component Analysis(PCA)

1：Maximum variance formulation：

1）：Maximum variance formulation的依据如下：数据正交投影到一个低维的线性空间，该低维线性空间的选择要使得投影数据的方差最大化，同时该低维线性空间也被称之为principal subspace；

2）：依据上述原理，我们能够获得如下的步骤去决定该低维(假设是M维)的线性空间：

(1)：计算数据集的协方差矩阵：

$$S=\frac{1}{N}\sum_{n=1}^{N}(\vec{x_{n}}-\bar{\vec{x}})(\vec{x_{n}}-\bar{\vec{x}})^{T}$$

(2)：计算其正交归一的本征矢量和对应的本征值，前M个最大的本征值所对应的本征矢量即为M维线性空间的基矢。并且投影到M维线性空间基矢的投影数据方差即为该基矢所对应的本征值；

(3)：假设M维线性空间的基矢分别为$\vec{u_{1}},...,\vec{u_{M}}$，则我们可以用$\widetilde{\vec{x_{n}}}=\sum_{m=1}^{M}(\vec{u}_{i}^{T}\vec{x_{n}})\ \vec{u}_{i}$去近似原先的数据点$\vec x$

2：Minimum-error formulation：

1)：Minimum-error formulation的依据如下：数据线性投影到低维的线性空间，该低维线性空间的选择要使得数据点与其投影的距离平方最小；

2)：依据此方法得出来的关于低维M维线性空间的选择与Maximum variance formulation的一样，都是选择协方差矩阵前M个最大本征值所对应的本征矢量；

3)：但有一点不同的是，当近似原先的数据点$\vec x$时，我们依据的是下式：

$$\widetilde{\vec{x_{n}}}=\sum_{i=1}^{M}(\vec{x}_{n}^{T}\vec{u}_{i})\vec{u}_{i}+\sum_{i=M+1}^{D}(\bar{\vec{x}}^{T}\vec{u}_{i})\vec{u}_{i} \\ =\bar{\vec{x}}+\sum_{m=1}^{M}(\vec{x}_{n}^{T}\vec{u}_{i}-\bar{\vec{x}}^{T}\vec{u}_{i})\vec{u}_{i}$$

3：Applications of PCA

1)：我们能够使用PCA对数据集进行转变，使得转变后的数据集平均值为0，协方差矩阵为单位协方差矩阵。步骤如下：

(1)：SU=UL，U是D*D正交矩阵，它的列由S的本征值$\vec{u}_{i}$组成，L是一个由本征值$\lambda_{i}$组成的D行D列的对角矩阵；

(2)：对原先数据集$\vec{x}_{n}$使用下式转变成$\vec{y}_{n}$：

$$\vec{y}_{n}=L^{-1/2}U^{T}(\vec{x}_{n}-\bar{\vec{x}})$$
可以证明，由 $\vec{y}_{n}$组成的数据集其均值为0，协方差为单位矩阵

2)：PCA和Fisher linear discriminant 都是用来维度缩减的，但要注意的是PCA属于未监督学习，其仅仅依赖于$\vec{x}_{n}$，而Fisher linear discriminat需要利用类标号信息。

3)：PCA能够被用来数据的可视化(data visualization)：每个数据点投影到两维的principal subspace，以至于每个数据点$\vec{x}_{n}$能够在两维坐标下显示，对应的坐标值为($\vec{x}_{n}^{T}\vec{u}_{1}$，$\vec{x}_{n}^{T}\vec{u}_{2}$)，$\vec{u}_{1}$和$\vec{u}_{2}$对应着第一大和第二大本征值的本征矢量。

4：PCA for high-dimensional data

1)：对于高维数据来说，假设是D维，计算其协方差矩阵的本征矢量所需要的计算量为O($D^{3}$)，计算量为很大；

2)：为了简化计算同时又能够计算出协方差矩阵所对应的本征矢量和本征值，我们能够按照如下步骤进行：

I：首先计算$XX^{T}$，X是N*D维矢量，其第n行为$(\vec{x}_{n}-\bar{\vec{x}})^{T}$；

II：利用下式计算$XX^{T}$本征矢量和对应的本征值：

$$\frac{1}{N}XX^{T}\vec{v}_{i}=\lambda_{i}\vec{v}_{i}$$

III：利用下式计算协方差矩阵的本征矢量：

$$\vec{u}_{i}=\frac{1}{(N\lambda_{i})^{1/2}}X^{T}\vec{v}_{i}$$ 对应的本征值依然是 $\lambda_{i}$

因为$XX^{T}$是N*N维，所以计算其本征值和对应的本征矢量所需要的计算为O($N^{3}$)，而不是刚开始的$O(D^{3})$

二：Probabilistic PCA

1：Probabilistic PCA的表达形式

1)：概率PCA属于线性高斯模型，其有一个对应着principal-component子空间的M维latent variable $\vec z$，满足的分布为$p(\vec z)=N(\vec z|0,I)$，条件在$\vec z$的D维observed variable $\vec x$所满足的分布为$p(\vec x|\vec z)=N(\vec x|W\vec z+\vec u,\sigma^{2}I)$，W是D*M矩阵并且可以证明W的列矢量对应着principal subspace；

2)：observed variable $\vec x$的边际分布$p(\vec x)$为$p(\vec x)=N(\vec x|\vec u,C),C=WW^{T}+\sigma^{2}I$；

3)：latent variable $\vec z$所满足的后验分布$p(\vec z|\vec x)$为$p(\vec z|\vec x)=N(\vec z|M^{-1}W^{T}(\vec x-\vec u),\sigma^{-2}M),M=W^{T}W+\sigma^{2}I$

2：Maximum likelihood PCA

1)：可以用极大似然法求解上述概率分布所含有的参数值$W,\vec u,\sigma$，得出来的结果如下：

$$\vec u=\frac{1}{N}\sum_{n=1}^{N}\vec{x}_{n} \\ W_{ML}=U_{M}(L_{M}-\sigma^{2}I)^{1/2}R \\ \sigma_{ML}^{2}=\frac{1}{D-M}\sum_{i=M+1}^{D}\lambda_{i}$$ 其中 $U_{M}$是D*M矩阵，其M个列矢量为协方差矩阵S前M个最大本征值所对应的本征矢量，所以W的列矢量定义了标准PCA的principal subspace。R为M维latent space的旋转矩阵，满足 $RR^{T}=1$，一般来说我们会将R设定为单位矩阵，因为R的选择对 $p(\vec x)$中的协方差矩阵C没有任何影响；

2)：传统PCA方法构造的思路是D维数据空间中数据点向M维线性空间的投影；然而概率PCA则要反过来，其被认为是M维latent space向数据空间的映射，映射的关系式是$\vec x=W\vec z+\vec u+\vec{\epsilon}$，其中$\vec{\epsilon}$是D维的均值为0，协方差矩阵为$\sigma^{2}I$的高斯分布噪音；

3)：当我们在应用概率PCA时，如果我们想要获得数据点在M维空间的投影，我们能够利用latent variable $\vec z$的后验分布，均值为$E[\vec z|\vec x]=M^{-1}W_{ML}^{T}(\vec x-\bar{\vec{x}})$，方差为不依赖于$\vec x$的$\sigma^{2}M^{-1}$。特别要注意的是如果我们采取极限$\sigma^{2}$趋于0，则后验平均值为$(W_{ML}^{T}W_{ML})^{-1}W_{ML}^{T}(\vec x-\bar{\vec{x}})$，这个代表了数据点在latent space的正交投影，因此此时我们恢复到了标准PCA模型；

4)：概率PCA模型不仅能够应用于维度缩减，同时它也定义了一个多变量的高斯分布$p(\vec x)$，此高斯分布不仅将独立参数的数目限定于与维度D呈线性关系的$DM+1-M(M-1)/2$，同时还能俘获变量成分与成分之间M个最显著的关联。

3：EM algorithm for PCA

1)：因为概率PCA包含latent variable $\vec z$，因此在求取概率PCA参数值时，我们可以用EM algorithm；

2)：我们首先初始化参数值，然后在E步与M步中迭代直至收敛标准被满足，在E步中所需要进行的计算为

$$E[\vec{z}_{n}]=M^{-1}W^{T}(\vec{x}_{n}-\bar{\vec{x}})\\ E[\vec{z}_{n}\vec{z}_{n}^{T}]=\sigma^{2}M^{-1}+E[\vec{z}_{n}]E[\vec{z}_{n}]^{T}$$ 在M步所需要的计算为 $$W_{new}=[\sum_{n=1}^{N}(\vec{x}_{n}-\bar{\vec{x}})E[\vec{z}_{n}]^{T}][\sum_{n=1}^{N}E[\vec{z}_{n}\vec{z}_{n}^{T}]]^{-1} \\ \sigma_{new}^{2}=\frac{1}{ND}\sum_{n=1}^{N}\{||\vec x_{n}-\bar{\vec{x}}||^{2}-2E[\vec{z}_{n}]^{T}W_{new}^{T}(\vec{x}_{n}-\bar{\vec{x}})+Tr(E[\vec{z}_{n}\vec{z}_{n}^{T}]W_{new}^{T}W_{new})\}$$

3)：如果我们采取$\sigma^{2}$趋于0的极限，则E step的计算可以简化为：

$$\Omega=(W_{old}^{T}W_{old})^{-1}W_{old}^{T}\widetilde{X}$$ M step的计算可以简化如下： $$W_{new}=\widetilde{X}^{T}\Omega^{T}(\Omega\Omega^{T})^{-1}$$ 其中 $\widetilde{X}$是N*D矩阵，第n行为 $(\vec{x}_{n}-\bar{\vec{x}})$， $\Omega$为D行M列矩阵，第n行为 $E[\vec{z}_{n}]$

4：Bayesian PCA

1)：如果我们只把参数当做点来处理的话，在应用概率PCA时我们必须要指定principal subspace的维度M，然而如果我们把M当做变量的话，并且归给予它一个合适先验，这样我们就能够让数据集自动的选择合适的维度M；

2)：W的先验被定为如下形式

$$p(W|\vec{\alpha})=\prod_{i=1}^{M}(\frac{\alpha_{i}}{2\pi})^{D/2}exp\{-\frac{1}{2}\alpha_{i}\vec{w}_{i}^{T}\vec{w}_{i}\}$$
这种先验的设定形式也是ARD(automatic relevance determination)的一种应用；

3)：由于最优化的结果，一些$\alpha_{i}$值会趋于无穷，这样就导致了其对应的$\vec{w}_{i}$值趋于0，因此principal subspace的有效维度由有限$\alpha_{i}$值的个数决定的。

5：Factor analysis

1：类似于概率PCA，Factor analysis也是一个线性高斯隐变量模型，但是条件在$\vec z$的$\vec x$高斯分布其方差不是各向同性的协方差$\sigma^{2}I$，而是对角化的协方差，表达形式如下：

$$p(\vec x|\vec z)=N(\vec x|W\vec z+\vec u,\Psi)$$

2：矩阵W被用来俘获观察变量之间的关联，其列矢量被称之为factor loadings；矩阵$\Psi$被用来代表每个变量本身拥有的与其它变量无关的噪音方差，其对角线元素被称之为uniquenesses；

3：观察变量$\vec x$的边际概率$p(\vec x)$为$p(\vec x)=N(\vec x|\vec u,C),C=WW^{T}+\Psi$

三：Kernel PCA

1：在$\vec x$空间中，有很大可能其principal subspace是非线性的，因此我们能够用函数$\vec{\phi}(\vec{x})$将最初的$\vec x$转化到特征空间中，然后在特征空间中principal subspace是线性的。然而我们并不想去确定函数$\vec{\phi}$的具体形式，在这时候我们可以利用kernel method；

2：kernel PCA的计算方法步骤如下：

I：利用下式计算矩阵$\widetilde{K}$：

$$\widetilde{K}=K-1_{N}K-K1_{N}+1_{N}K1_{N}$$ $1_{N}$表示每个元素都为1/N的N*N矩阵；

II：利用$\widetilde{K}\vec{a}_{i}=\lambda_{i}N\vec{a}_{i}$以及$\lambda_{i}N\vec{a}_{i}^{T}\vec{a}_{i}=1$这两个条件计算其本征值$\lambda_{i}$和$\vec{a}_{i}$；

III：数据点$\vec x$在用函数$\vec{\phi}$转换后数据集协方差矩阵的第i个本征矢量的投影为$y_{i}(\vec x)=\sum_{n=1}^{N}a_{in}k(\vec x,\vec{x}_{n})$

3：在标准线性PCA中，我们会用$\widetilde{\vec{x}_{n}}=\sum_{i=1}^{M}(\vec{x}_{n}^{T}\vec{u}_{i})\vec{u}_{i}$来近似原先的数据点$\vec{x}_{n}$，但是在kernel PCA中这是不可能的。

四：Nonlinear Latent Variable Models

1：Independent component analysis

1)：observed variables与latent variables是线性相关的，例如$\vec{x}=A\vec{z}$，然而latent variables是非高斯分布，其各个成分之间的概率分布是相互独立的，具有如下的因式分解形式：

$$p(\vec z)=\prod_{j=1}^{M}p(z_{j})$$ $p(z_{j})$经常被选择如下的形式： $$p(z_{j})=\frac{1}{\pi(e^{z_{j}}+e^{-z_{j}})}$$

2)：假设观察变量$\vec{x}$与隐变量$\vec{z}$满足关系式$\vec{x}=A\vec{z}$，现在我们有了观察的数据集$\{\vec{x}_{i}\}$以及概率分布$p(\vec z)$的具体形式(也就是有了观察变量$p(\vec x)$的具体形式)，则我们可以通过极大似然法获得矩阵A的值，因此我们也就有了$\vec z$的值，在这种情况下，我们能够应用ICA。如果我们应用PCA，也就是说假定$\vec z$满足的是高斯分布，正如我们之前看到的，矩阵A和矩阵AR($RR^{T}=1$)所导致的$\vec x$的概率分布是一样的，因此我们无法知道矩阵A的恰好形式，因此也就无法得知$\vec{z}$的值。

2：Autoassociative neural networks

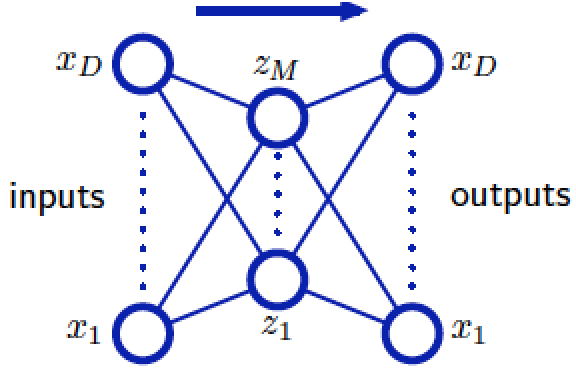
1)：Autoassociative neural networks有相同的D个输入和D个输出，有M个hidden units($M<D$)，用来训练网络的目标矢量就是输入变量自身，以便于神经网络尝试把每个输入矢量映射到它本身以此减小reconstruction error，最小化的目标函数如下：

$$E(\vec{w})=\frac{1}{2}\sum_{n=1}^{N}||\vec{y}(\vec{x}_{n},\vec{w})-\vec{x}_{n})||^{2}$$

2)：如果说只有一个hidden layer（如下图），那么autoassociative neural networks相当于linear dimensionality reduction，从输入层连接hidden units的权重矢量就形成了扩展linear principal subspace的一组基集，hidden layer各units的值就相当于数据点在此principal subspace的投影值；

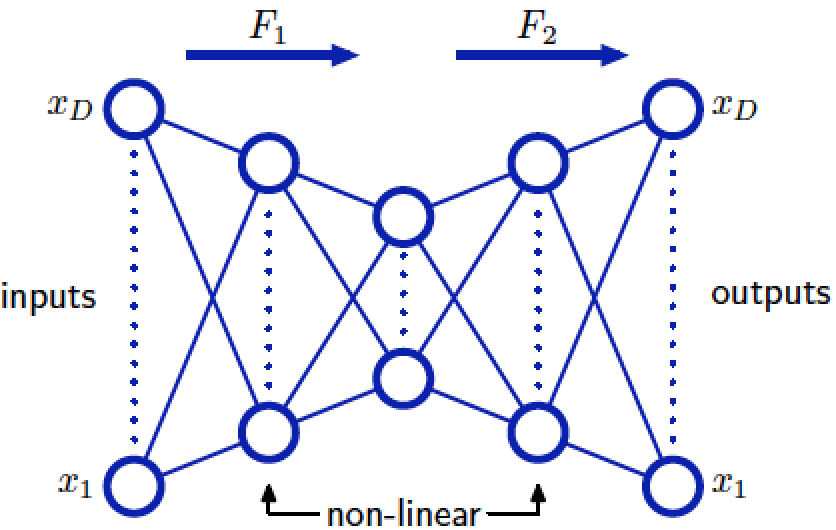
3)：如果说在上述的神经网络基础上再添加两个hidden layer（如下图），并且第一个和第三个hidden layer units的activation functions是sigmoidal非线性的，那么这就相当于nonlinear dimensionality reduction。