gls开发_广义最小二乘gls数学推导直觉

gls开发

背景与动机(Background and Motivation)

For anyone pursuing study in Statistics or Machine Learning, Ordinary Least Squares (OLS) Linear Regression is one of the first and most “simple” methods one is exposed to. However, there are a set of mathematical restrictions under which the OLS estimator is the Best Linear Unbiased Estimator (BLUE), i.e. the unbiased estimator with minimal sampling variance. (For a more thorough overview of OLS, the BLUE, and the Gauss-Markov Theorem, please see my previous piece on the subject)

对于那些追求统计学或机器学习的人来说，普通最小二乘(OLS)线性回归是人们最早接触到的“最简单”方法之一。 但是，存在一组数学限制，在这些数学限制下，OLS估计器是最佳线性无偏估计器(BLUE)，即具有最小采样方差的无偏估计器。 (有关OLS，BLUE和Gauss-Markov定理的更全面概述，请参阅我关于该主题的上一篇文章)

What if the mathematical assumptions for the OLS being the BLUE do not hold? The next “leap” is Generalized Least Squares (GLS), of which the OLS is in fact a special case of. This article serves as an introduction to GLS, with the following topics covered:

如果OLS为BLUE的数学假设不成立怎么办？ 下一个“跳跃”是广义最小二乘(GLS) ，而OLS实际上是其中的一个特例。 本文是GLS的简介，涵盖了以下主题：

1. Review of the OLS estimator and conditions required for it to be BLUE
   审查OLS估计量及其变为蓝色所需的条件
2. Mathematical set-up for Generalized Least Squares (GLS)
   广义最小二乘(GLS)的数学设置
3. Recovering the GLS estimator
   恢复GLS估算器
4. Proof that the GLS Estimator is Unbiased
   GLS估计器无偏的证明
5. Recovering the variance of the GLS estimator
   恢复GLS估计量的方差
6. Short discussion on relation to Weighted Least Squares (WLS)
   关于加权最小二乘(WLS)的简短讨论

Note, that in this article I am working from a Frequentist paradigm (as opposed to a Bayesian paradigm), mostly as a matter of convenience. So, let’s jump in:

请注意，在本文中，我主要是基于“惯常”范式(而不是贝叶斯范式)进行的。 因此，让我们进入：

1.审查OLS估计量及其为BLUE的条件 (1. Review of the OLS estimator and conditions for it being the BLUE)

Let’s start with a quick review of the OLS estimator

让我们先快速回顾一下OLS估算器

Image by Author

图片作者

For further information on the OLS estimator and proof that it’s unbiased, please see my previous piece on the subject.

有关OLS估计器的更多信息并证明它没有偏见，请参阅我上一篇有关该主题的文章。

2.广义最小二乘(GLS)的数学设置 (2. Mathematical set-up for Generalized Least Squares (GLS))

Image by Author

图片作者

3.恢复GLS估算器(3. Recovering the GLS estimator)

Image by Author

图片作者

4.证明GLS估计是无偏的(4. Proof that the GLS Estimator is Unbiased)

Image by Author

图片作者

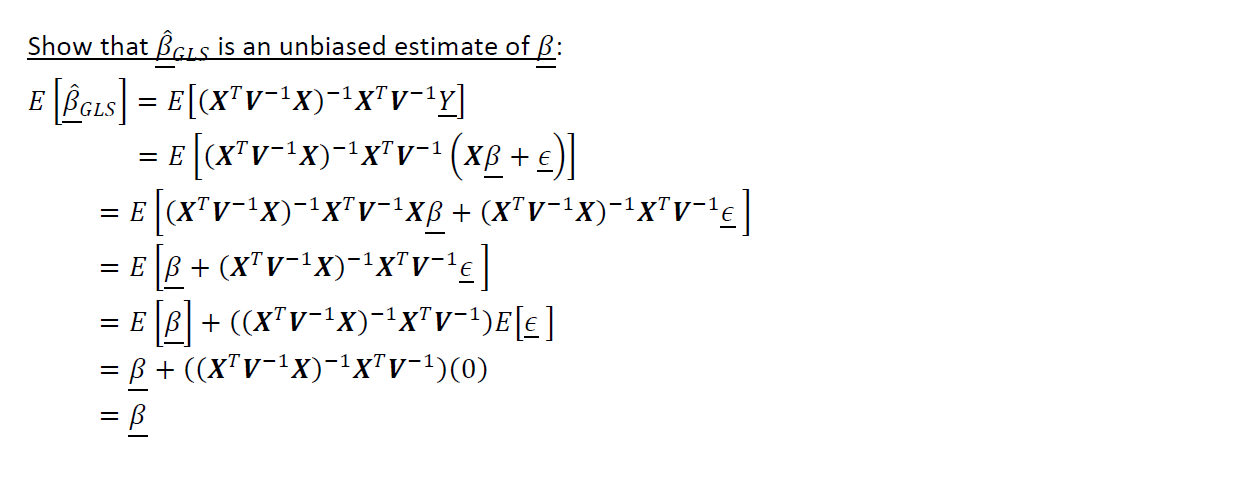
5.恢复GLS估计量的方差(5. Recovering the variance of the GLS estimator)

Image by Author

图片作者

6.关于加权最小二乘(WLS)的简短讨论(6. Short discussion on relation to Weighted Least Squares (WLS))

Image by Author

图片作者

总结，最后的想法和后续步骤(Wrap-up, Final Thoughts, and Next Steps)

Generalized Least Squares (GLS) is a large topic. This article serves as a short introduction meant to “set the scene” for GLS mathematically. There’s plenty more to be covered, including (but not limited to):

广义最小二乘(GLS)是一个大话题。 本文只是一个简短的介绍，旨在通过数学方式为GLS“设置场景”。 还有更多内容要涵盖，包括(但不限于)：

1. A more in-depth dive into WLS
   更深入地探讨WLS

2. Methods and approaches for specifying covariance matrix V

   指定协方差矩阵V的方法和方法

3. The topic of Feasible Generalized Least Squares
   可行广义最小二乘法
4. Relation to Iteratively Reweighted Least Squares (IRLS)
   与迭代加权最小二乘(IRLS)的关系

I plan on covering these topics in-depth in future pieces.

我计划在以后的文章中深入介绍这些主题。

I hope the above is insightful and helpful. As I’ve mentioned in some of my previous pieces, it’s my opinion not enough folks take the time to go through these types of exercises. For me, this type of theory-based insight leaves me more comfortable using methods in practice. A personal goal of mine is to encourage others in the field to take a similar approach. I’m planning on writing similar theory based pieces in the future, so feel free to follow me for updates!

我希望以上内容能为您提供有益的见解和帮助。 正如我在前几篇文章中提到的那样，我认为没有足够的人花时间进行这些类型的练习。 对我而言，这种基于理论的见解使我在实践中使用方法更加自在。 我的个人目标是鼓励该领域的其他人采取类似的方法。 我打算将来写类似的基于理论的文章，​​所以随时关注我进行更新！

翻译自: https://towardsdatascience.com/generalized-least-squares-gls-mathematical-derivations-intuition-2b7466832c2c

gls开发