线性插值和二次插值_插值参数模型的线性回归连接和重要主题

最新推荐文章于 2023-10-29 18:48:03 发布

李_涛

最新推荐文章于 2023-10-29 18:48:03 发布

阅读量5.6k

点赞数

文章标签： python 机器学习 tensorflow java 深度学习

原文链接：https://medium.com/analytics-vidhya/linear-regression-connection-with-interpolation-parametric-model-and-important-topics-for-513d7d4f9c5f

版权

线性插值和二次插值

The model may turn out to be far too complex if we continuously keep adding more variables.

如果我们不断增加更多的变量，该模型可能会变得过于复杂。

Will fail to simplify as it is memorizing the training data.

记住训练数据将无法简化。

We say Model is over-fitting when the accuracy is high in Training and the accuracy of Test is very low

我们说当训练中的准确性高而测试的准确性很低时，模型就过度拟合

多重共线性： (Multicollinearity:)

Associations between predictor variables. Single Variable collinearity can be existing with two or more variable even if no pair of variables has a high correlation.

预测变量之间的关联。即使没有一对变量具有高相关性，也可以存在两个或多个变量的单变量共线性。

Multicollinearity affects when we are trying to interpret the model, we can avoid by checking Pairwise Correlations and by Variance Inflation Factor (VIF) value.

多重共线性会影响我们尝试解释模型时的效果，我们可以通过检查成对相关性和方差膨胀因子 (VIF)值来避免这种情况。

The common experimental we follow for the VIF values is:

我们遵循的有关VIF值的常见实验是：

>10: Definitely high VIF value and the variable should be eliminated.

> 10：绝对高的VIF值，并且应消除该变量。

> 5: Can be okay, but it is worth inspecting.

> 5：可以，但是值得检查。

< 5: Good VIF value. No need to eliminate this variable.

<5：良好的VIF值。 无需消除此变量。

通过创建虚拟变量来处理分类变量-级别更少 (Dealing with categorical variables by creating Dummy variables — for fewer levels)

功能缩放： (Feature Scaling:)

We can Standardisation, MinMax scaling and Scaling for categorical variables which mostly makes all the data into a standard normal distribution.

我们可以对分类变量进行标准化，MinMax缩放和缩放，这些变量大部分会使所有数据变成标准正态分布。

模型评估和比较： (Model Assessment and Comparison:)

Adjusted R-squared, AIC and BIC are being used for Penalizing the model for using larger number of variables. In the below equation P is number of variables

调整后的R平方，AIC和BIC用于对使用大量变量的模型进行惩罚。在下面的公式中P是变量的数量

功能选择： (Feature Selection:)

We can do Manual feature selection (Top Down / Bottom up approach) or else Automated feature selection (RFE — Recursive feature elimination) choosing either the best or worst performing feature. We can find a balance between the above two approaches.

我们可以执行手动功能选择 (自上而下/自底向上方法)，也可以执行自动功能选择 ( RFE- 递归功能消除 )，以选择性能最佳或最差的功能。我们可以在上述两种方法之间找到平衡。

With the help of Hypothesis testing on the beta coefficient we can check whether the coefficient is significant or not using p-values.

借助对β系数的假设检验，我们可以使用p值检查系数是否显着。

火车数据的残差分析： (Residual Analysis of the train data:)

Need to check if the error terms are also normally distributed it is one of the major statements of linear regression.

需要检查误差项是否也正态分布，这是线性回归的主要陈述之一。

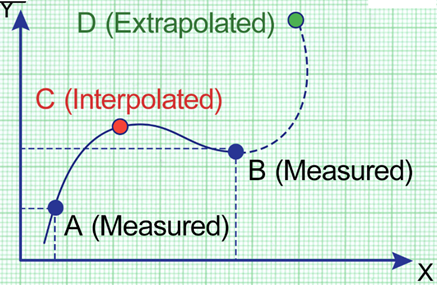
回归保证数据的内插而不是外推： (Regression promises Interpolation of data and not Extrapolation:)

Interpolation means applying the model to predict the value of a dependent variable on independent values that lie within the range of data already we have for analysis.

插值法是指应用模型来预测因变量而导致的因变量值，这些值位于我们已经进行分析的数据范围内。

Extrapolation means predicting the dependent variable on the independent values that lie outside the range of the data.

外推意味着根据数据范围之外的独立值预测因变量。

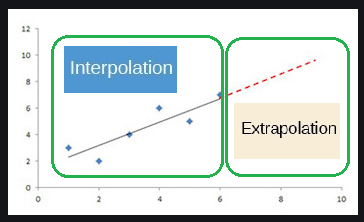
So, whenever the new data comes in Extrapolation section, model will not be able to understand pattern of the graph if it is having different trend so the difference between predicted value and the actual value will be high.

因此，每当新数据进入“外推”部分时，如果模型具有不同的趋势，模型将无法理解图形的模式，因此预测值和实际值之间的差异会很大。

线性回归是一个参数模型，可抵抗非参数模型： (linear Regression is a parametric model and resisted to non-parametric ones:)

A parametric model can be described using a finite number of parameters. In a linear regression model built using N independent variables will have exactly N ‘parameters’ (i.e. the N coefficients). The entire model can be described using these N parameters.

可以使用有限数量的参数来描述参数模型。在使用N个独立变量构建的线性回归模型中，将具有N个“参数”(即N个系数)。可以使用这N个参数来描述整个模型。

考虑通过线性回归进行的预测和投影/预测： (Considering Prediction and Projection/Forecasting through Linear Regression:)

We must consider “Predictor Variables and generating Simple Model is more important in case of Prediction” whereas “Forecasted value is more important than predictor variable with High Accuracy in case of Projection/Forecasting as we don’t require to do the explanation”

我们必须考虑“在预测的情况下，预测变量和生成简单模型更为重要 ”，而“ 在投影/预测的情况下，预测值比具有高精度的预测变量更重要，因为我们不需要做解释”

https://machinelearningmastery.com/parametric-and-nonparametric-machine-learning-algorithms/

https://stats.stackexchange.com/questions/268638/what-exactly-is-the-difference-between-a-parametric-and-non-parametric-model

https://www.datarobot.com/wiki/overfitting/

https://sciencestruck.com/interpolation-vs-extrapolation