big o_big o 101简单介绍

big o

The classical definition for Big O according to Wikipedia is:

根据维基百科，Big O的经典定义是：

Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity.

大O表示法是一种数学表示法，用于描述参数趋于特定值或无穷大时函数的限制行为。

There are a lot of concepts within this definition and that’s probably why a lot of people are afraid of Big O. In a few words, we use Big O to describe the performance of an algorithm. This helps us determine wether and if an algorithm is scalable or not. This means: will this algorithm continue to perform even if the input gets really really large ? The truth is that most of the time we assume that because our code runs fast on our computer it will run equally as fast when giving a larger input. However this is not the case at all. That’s why we use Big O notation to describe the performance of an algorithm. This is extremely important when dealing with choosing what data structure to use. Some operations can be more or less costly depending on what data structure we use. For example, accessing an array by its index is super fast but arrays have a fixed length. Meaning that they need to get re-sized every time we add an element. This can get very costly if we have a large input. Let’s get to some examples!

这个定义中有很多概念，这可能就是为什么很多人都害怕Big O的原因。简而言之，我们使用Big O来描述算法的性能。 这有助于我们确定算法是否可扩展以及是否可扩展。 这意味着：即使输入变得非常大，该算法也会继续执行吗？ 事实是，大多数时候我们都认为由于代码在计算机上运行的很快，因此在提供较大的输入时，其运行速度也一样快。 但是，事实并非如此。 这就是为什么我们使用Big O表示法来描述算法的性能。 在选择要使用的数据结构时，这非常重要。 根据我们使用的数据结构，某些操作的成本或高或低。 例如，通过数组的索引访问数组非常快，但是数组的长度是固定的。 意味着每次我们添加元素时都需要调整大小。 如果我们投入大量资金，这可能会非常昂贵。 让我们来看一些例子！

O(1)： (O(1):)

public class Main {
  public void log(int[] numbers) {
   System.out.println(numbers[0]);
  }
}

This method takes an array of integers and prints the first item in the console. In this case, it doesn’t matter how big the array is. We are still just printing the first item of the array. This method has a single operation and takes a constant amount of time to run. Because of that, we represent this constant time of execution by saying that this method has a Big O of 1 or O(1). In this example, the size of the input does not matter, this method will always run in constant time or in Big 0 of 1. Now, what if we have two, three or a hundred operations that execute in constant time ?

此方法采用整数数组，并在控制台中打印第一项。 在这种情况下，数组的大小无关紧要。 我们仍然只是打印数组的第一项。 此方法具有单个操作，并且需要固定的时间运行。 因此，我们通过说此方法的Big O为1或O(1)来表示这个恒定的执行时间。 在此示例中，输入的大小无关紧要，该方法将始终以恒定时间或以1的大0运行。现在，如果我们有两个，三个或一百个在恒定时间内执行的操作，该怎么办？

public class Main {
  public void log(int[] numbers) {
   System.out.println(numbers[0]);   
   System.out.println(numbers[0]);
   System.out.println(numbers[0]);
  }
 }

In this case, it almost seems obvious to think that you would describe this method as Big O of 3 or O(3). However, when talking about the runtime complexity we don’t really care about the number of operations, we just want to know how much does an algorithm slows down as the input grows. So, in this example whether we have one, three or a million items, our method runs in constant time or Big O(1).

在这种情况下，似乎很明显认为您会将这种方法描述为Big O of 3或O(3)。 但是，在谈论运行时复杂性时，我们并不真正在乎操作的数量，我们只想知道算法随着输入的增长会减慢多少。 因此，在此示例中，无论我们有一个，三个或一百万个项目，我们的方法都以固定时间或Big O(1)运行。

上)： (O(n):)

Here we have a slightly more complex example:

这里有一个稍微复杂的例子：

public class Main {
  public void log(int[] numbers) {
   for (int i = 0; i < numbers.length; i++) {
    System.out.println(numbers[i]);
   }
  }
 }

We have a loop! We are iterating over all the items of the array and printing each item on the console. This is when the size of the input matters. If we have a single item we are going to have one print operation, if we have a million items we are going to have a million print operations. So the cost of this algorithms grows linearly and in direct correlation to the size of the input. We represent the runtime complexity of this algorithm as 0(n), where n represents the size of the input. As n grows the cost grows as well.

我们有一个循环！ 我们正在遍历数组的所有项目并在控制台上打印每个项目。 这是输入大小重要的时候。 如果我们只有一个项目，那么我们将进行一次打印操作；如果我们有一百万个项目，那么我们将进行一百万打印操作。 因此，这种算法的成本与输入的大小呈线性增长并成正比。 我们将该算法的运行时复杂度表示为0(n)，其中n表示输入的大小。 随着n的增长，成本也随之增长。

O(n²)： (O(n²):)

In the previous example we went over a single loop, but what if we have nested loops ?

在前面的示例中，我们经历了一个循环，但是如果我们有嵌套循环，该怎么办？

public class Main {
  public void log(int [] numbers) {
   for (int first : numbers)
    for (int second : numbers)
     System.out.println(first + ", " + second);
  }
 }

In both loops, we are iterating over all the items of the array. Meaning, that both the outer loop and the inner loop have a runtime complexity of 0(n). The runtime complexity of the function as a whole would be O(n²). Because of this ,we say this algorithm runs in quadratic time.

在两个循环中，我们都在遍历数组的所有项目。 这意味着，外循环和内循环的运行时复杂度均为0(n)。 整个函数的运行时复杂度为O(n²)。 因此，我们说该算法以二次时间运行。

Quadratic vs Linear

二次方与线性

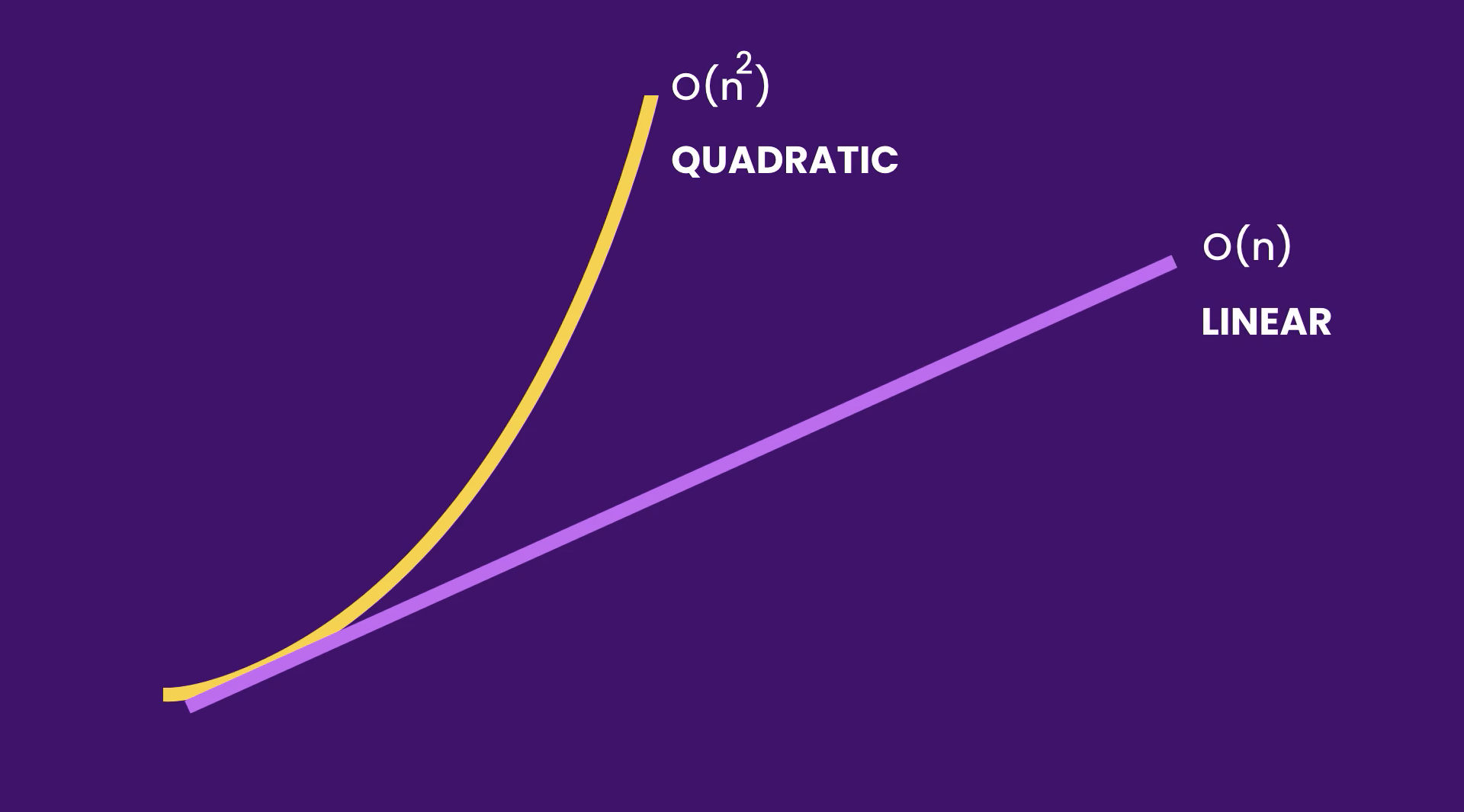
Algorithms that run in O(n²) run slower than algorithms that run in O(n). Of course, this depends on the size of the input. If you were to run both functions with an array of 50 items most likely there wouldn’t be any difference in time. But as the input runs larger and larger, algorithms that run in O(n²) get slower and slower.

以O(n²)运行的算法的运行速度比以O(n)运行的算法慢。 当然，这取决于输入的大小。 如果您要同时运行包含50个项目的两个函数，则时间不会有任何差异。 但是随着输入越来越大，以O(n²)运行的算法越来越慢。

O(log n)： (O(log n):)

The last growth rate we are going to talk about is the logarithmic growth which we show as O(log n). An algorithm that runs in logarithmic time is more scalable that an algorithm that runs in linear or quadratic time.

我们要讨论的最后一个增长率是对数增长率，我们将其表示为O(log n)。 以对数时间运行的算法比以线性或二次时间运行的算法更具扩展性。

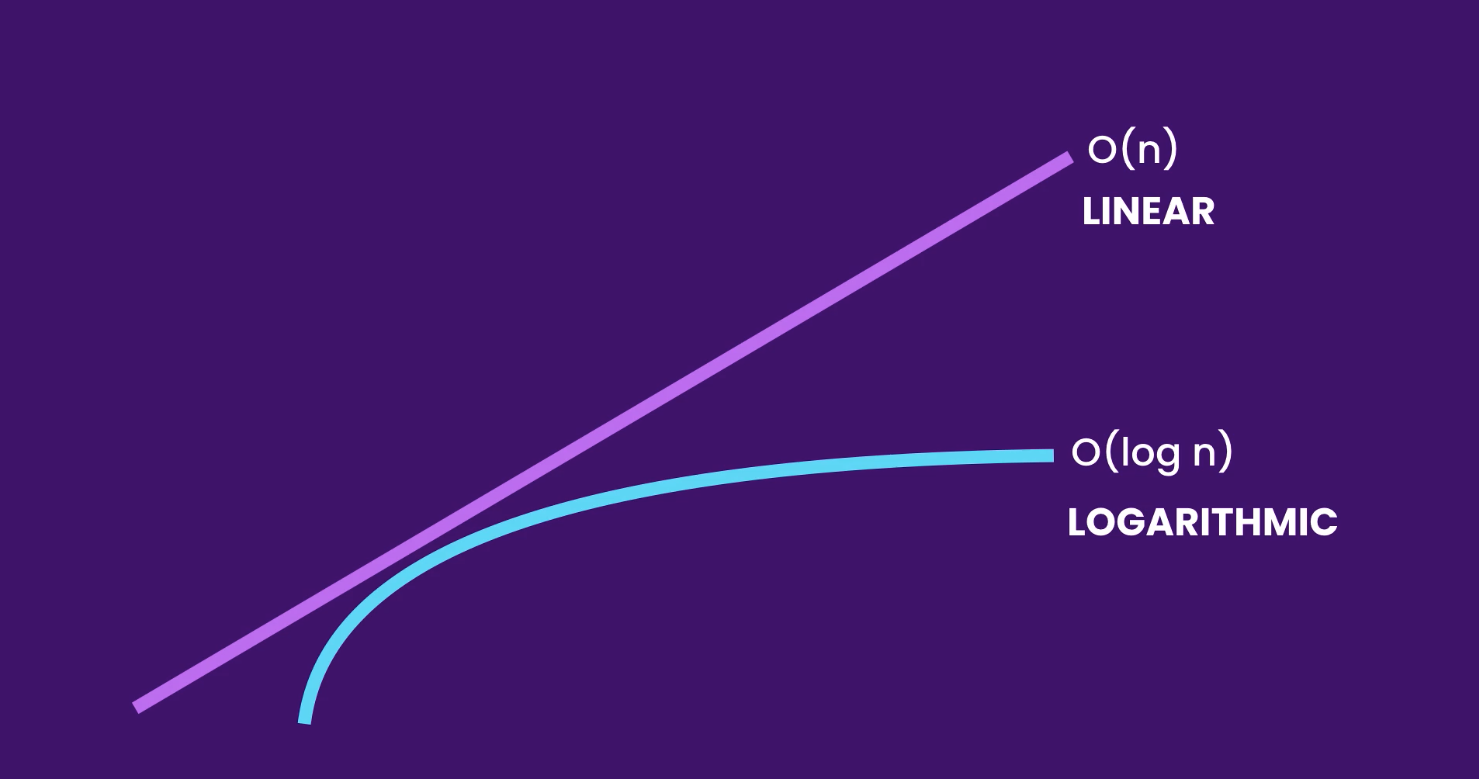
As you can see above, contrary to the linear curve the logarithmic curve slows down at some point. An easy example to show this is to compare linear search with binary search. Let’s say we have an array of sorted numbers from 1 to 10 and we want to find the number 10. One way to find the 10 is to use linear search. We would need to iterate over each item of the array until we find the number 10. Now, in order for us to find the number 10 we would need to check each element in the array and this can get costly very fast. The more elements we have, the more this operation is going to take. The runtime complexity of this algorithm increases linearly and in direct proportion with the input. On the other hand, we have binary search which runs in logarithmic time. This is much faster than the linear search. Assuming the array is sorted we start by looking at number in the middle and checking if its smaller or larger that the value we are looking for. Since 5 is smaller than 10, we now look at the right portion of the array and do the same. We continue with this pattern narrowing the search in half each time. With this algorithm, if we have an array of one million items, we can find the target value with a maximum of 19 comparisons.

如上所示，与线性曲线相反，对数曲线在某些点处变慢。 一个简单的例子表明，比较线性搜索和二进制搜索。 假设我们有一个从1到10的排序数字数组，我们想找到数字10。找到10的一种方法是使用线性搜索。 我们需要遍历数组的每个项目，直到找到数字10。现在，为了找到数字10，我们需要检查数组中的每个元素，这可能会非常快速地耗费成本。 我们拥有的元素越多，此操作将花费的越多。 该算法的运行时复杂度与输入线性增加并成正比。 另一方面，我们有以对数时间运行的二进制搜索。 这比线性搜索快得多。 假设对数组进行排序，我们首先查看中间的数字，然后检查其是否小于或大于我们要查找的值。 由于5小于10，因此我们现在看一下数组的右侧部分并执行相同的操作。 我们继续使用此模式，每次将搜索范围缩小一半。 使用此算法，如果我们有一百万个项目的数组，我们最多可以找到19个比较的目标值。

I hope this cleared out the concept of Big O a little more and that now you can start thinking about runtime complexity when designing new algorithms. Stay tuned for a second part on Big O! Happy coding.

我希望这可以进一步澄清Big O的概念，现在您可以在设计新算法时开始考虑运行时复杂性。 敬请关注Big O的第二部分！ 快乐的编码。

翻译自: https://medium.com/@emilioquintana90/big-o-101-an-easy-introduction-84567a4fe46d

big o