神经网络不是黑匣子

If you think neural nets are black boxes, you’re certainly not alone. While they may not be as interpretable as something like a random forest (at least not yet), we can still understand how they process data to arrive at their predictions. In this post we’ll do just that as we build our own network from scratch, starting with logistic regression.

如果您认为神经网络是黑匣子，那么您肯定并不孤单。 尽管它们可能不像随机森林那样具有可解释性(至少目前还没有)，但我们仍然可以理解它们如何处理数据以得出预测。 在本文中，我们将从逻辑回归开始，从头开始构建我们自己的网络。

This post is very much inspired by this fantastic post by Sylvain Gugger. We won’t pretend to improve upon Sylvain’s post; we just want to explain things in our own way to help us understand things a little better. This post is the first of a series of posts in which we’ll build our own DNN, CNN, and RNN in numpy. You can find all of the source code at tinytorch.

这篇文章的灵感来自Sylvain Gugger的精彩文章 。 我们不会假装改善Sylvain的职位； 我们只是想以自己的方式解释事物，以帮助我们更好地理解事物。 这篇文章是一系列文章的第一篇，我们将在numpy构建自己的DNN，CNN和RNN。 您可以在tinytorch上找到所有源代码。

目的 (Objective)

Our goal is to construct a binary logistic classifier as a neural network. The network will consist of a single linear layer followed by a sigmoid activation with binary cross entropy as the loss. We’ll begin by deriving the back-prop equations for our particular scenario and in doing so we’ll see that what we’ve done generalizes immediately to networks with arbitrary layers and activations. In other words, we’ll have developed a framework that can model any feedforward network — all by starting from ordinary logistic regression.

我们的目标是将二进制逻辑分类器构造为神经网络。 该网络将由单个线性层组成，然后是S型激活，并以二进制交叉熵作为损耗。 我们将首先针对特定场景推导反向支持方程，然后我们将看到所做的工作可以立即推广到具有任意层和激活的网络。 换句话说，我们将开发一个可以对任何前馈网络进行建模的框架-所有这些都是从普通的逻辑回归开始的。

Actually, this isn’t all that surprising when you think about it. Logistic regression is a linear layer followed by sigmoid and feedforward networks are just a bunch of linear layers stacked together with non-linearities in between.

实际上，当您考虑它时，这并不奇怪。 Logistic回归是一个线性层，其后是S型曲线，前馈网络只是一堆线性层，中间堆叠着非线性。

反向传播 (Back-propagation)

Back-propagation is nothing more than the chain rule. We can view our logistic network as the composition of three functions

反向传播无非就是链式规则。 我们可以将物流网络视为三个职能的组成

While the loss function is not usually viewed as a layer of the network, treating it as the final layer makes computing the gradients easier. Let’s denote the output of the i-th layer by xi so that

虽然通常不会将损失函数视为网络的一层，但将其视为最终层会使计算梯度变得更加容易。 让我们用xi表示第i层的输出

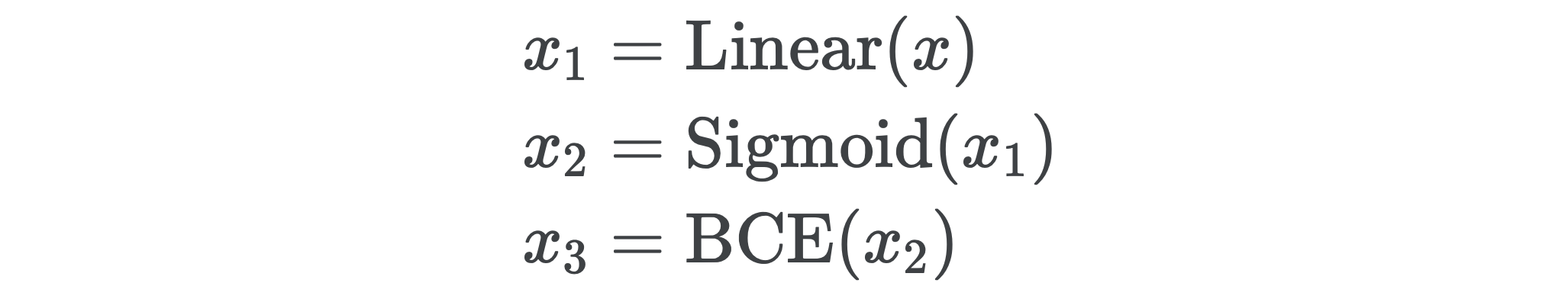
The first gradient we have to compute is the gradient of BCE with respect to the activations x2.

我们必须计算的第一个梯度是BCE相对于激活x2的梯度。

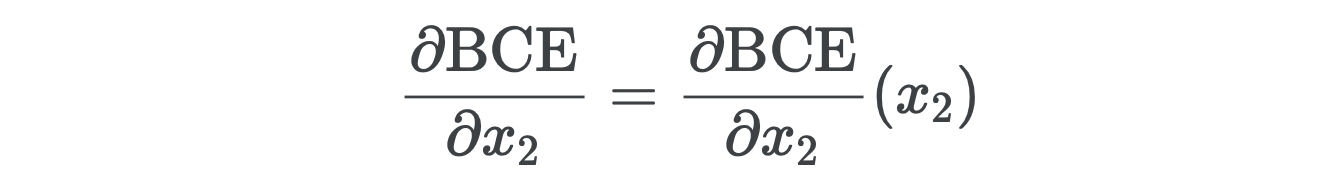
Next we have to compute the gradient with respect to the linear outputs x1. The chain rule tells us

接下来，我们必须计算相对于线性输出x1的梯度。 连锁规则告诉我们

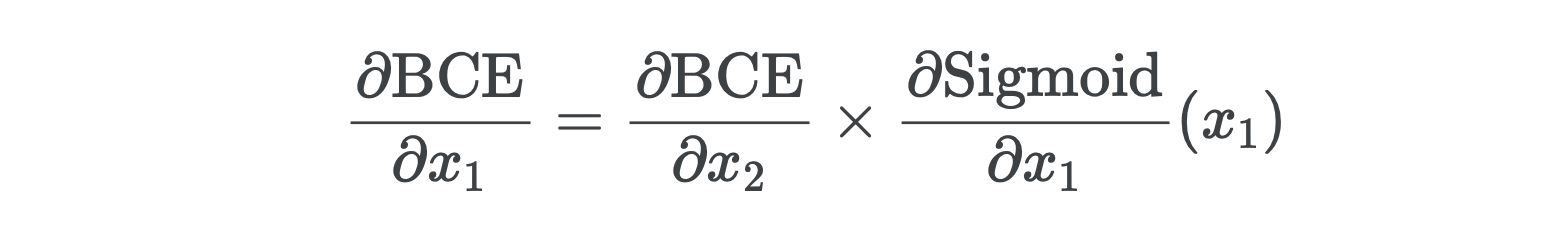
Last, we’ll need the gradient with respect to the original inputs x.

最后，我们需要相对于原始输入x的渐变。

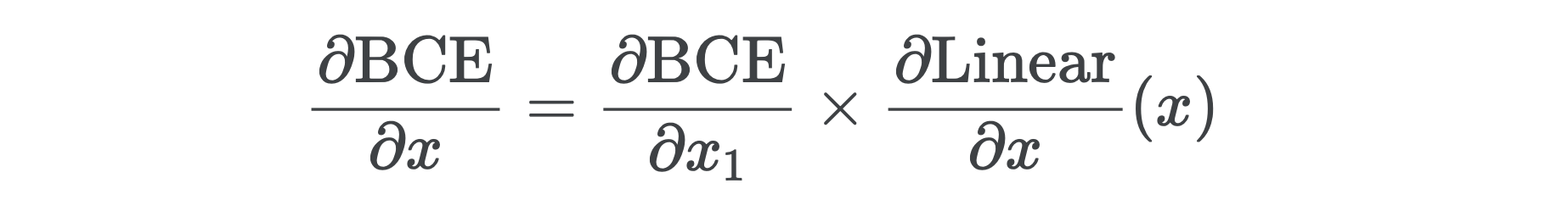
Notice a pattern? The first gradient we computed — the gradient with respect to the network’s final activations — is used to compute the next gradient — the gradient with respect to the linear outputs — which is in turn used to compute the gradient with respect to the original inputs. To compute the gradients of any network, we simply start at the last layer and successively pass the gradients backwards to the preceding layer until we arrive at the original inputs. That’s the reason it’s called back-propagation. It really is helpful to picture passing the gradients backwards through the network like a baton.

注意到模式吗？ 我们计算的第一个梯度-相对于网络最终激活的梯度-用于计算下一个梯度-相对于线性输出的梯度-反过来又用于计算相对于原始输入的梯度。 要计算任何网络的梯度，我们只需从最后一层开始，然后将梯度连续地向后传递到上一层，直到到达原始输入。 这就是所谓的反向传播的原因。 将渐变像警棍一样通过网络向后传递，确实很有帮助。

We’ll compute each of these gradients in turn, starting with the last layer and working our way backwards to the original inputs.

我们将从上一层开始依次计算这些梯度中的每一个，然后逐步返回原始输入。

⚠️ Note: So far we’ve been treating the input x as a single variable, but most of the time x will have more than one dimension. Computing the gradients in the multi-variate case isn’t any more difficult than what we’ve done (it involves something called the Jacobian, but we’ll pretend we didn’t hear that).

Note️注意：到目前为止，我们一直将输入x视为一个变量，但是大多数时候x会具有多个维度。 在多变量情况下计算梯度并不比我们所做的困难(它涉及称为Jacobian的事情，但我们会假装没有听到)。

二元交叉熵 (Binary Cross Entropy)

Binary cross entropy penalizes predictions by the logarithm of their confidence. Given labels y which are either zero or one and probabilities y_hat for the positive class, binary cross entropy is computed as

二进制交叉熵通过其置信度的对数惩罚预测。 给定标签y为零或一个，并且y_hat正类的概率y_hat ，则二进制交叉熵计算为

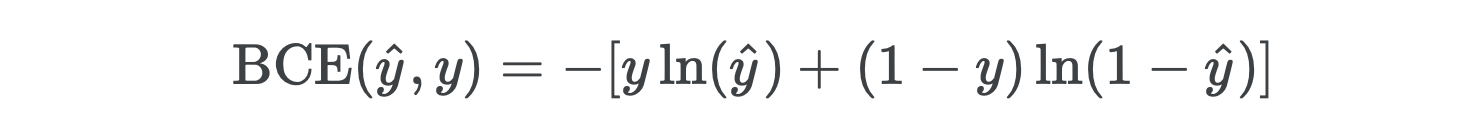
After simplifying, you’ll find its derivative is

简化后，您会发现其派生词是

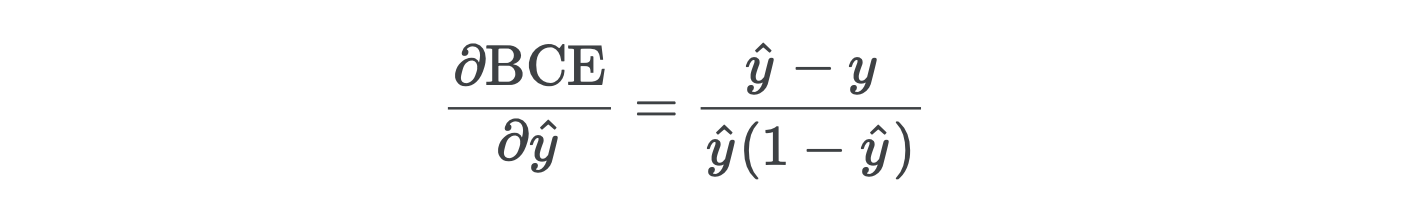
To avoid division-by-zero errors, we’ll clip the probabilities so that they’re not too close to zero or one.

为了避免被零除的错误，我们将裁剪概率，以使它们不太接近零或一。

激活方式 (Activations)

The easiest components of networks to handle are the activation functions. Our activation is sigmoid, which you’ll often see defined as one of

网络最容易处理的组件是激活功能。 我们的激活是乙状结肠，您经常会看到它被定义为

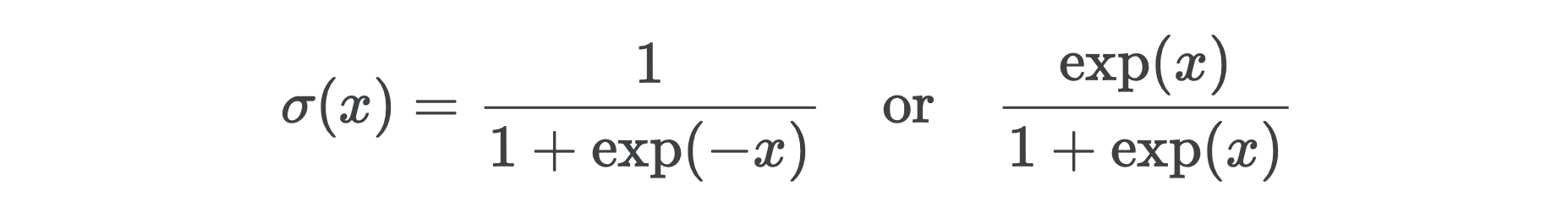
It turns out we need both versions to implement a numerically stable sigmoid. Why? Notice how when x is very negative, exp(−x) is very large, and when x is very positive, exp(x) is very large — in both cases too large to store in memory. The easy fix is to use the former when x>0 and the latter when x<0.

事实证明，我们需要两种版本来实现数值稳定的S型。 为什么？ 请注意，当x非常负时， exp(−x)很大，而当x非常正时， exp(x)很大–在两种情况下都太大而无法存储在内存中。 简单的解决方法是在x>0时使用前者，在x<0时使用后者。

After simplifying, you’ll find the derivative of sigmoid is

简化后，您会发现Sigmoid的导数为

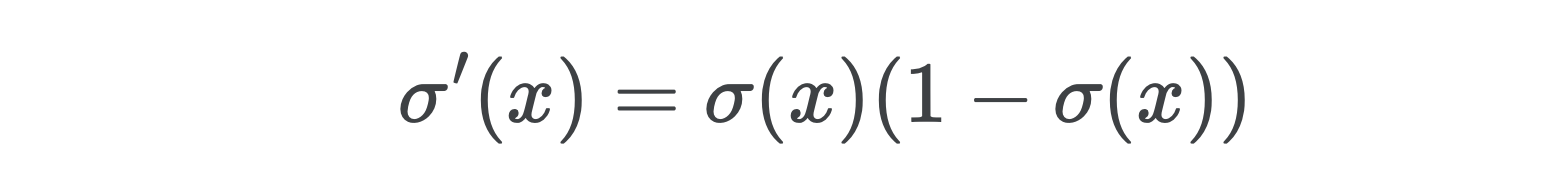
Notice something interesting? Since we denoted y_hat as the output of sigmoid, this is exactly the denominator of the BCE gradient we computed above, meaning the two terms will cancel when multiplied, which is what the chain rule tells us will happen when we compute the gradient with respect to the outputs x1 of our network’s last (and only) linear layer.

注意一些有趣的东西吗？ 由于我们将y_hat表示为y_hat的输出，因此这恰好是我们上面计算的BCE梯度的分母，这意味着当相乘时这两个项将抵消，这是链规则告诉我们在计算相对于网络最后(也是唯一)线性层的输出x1 。

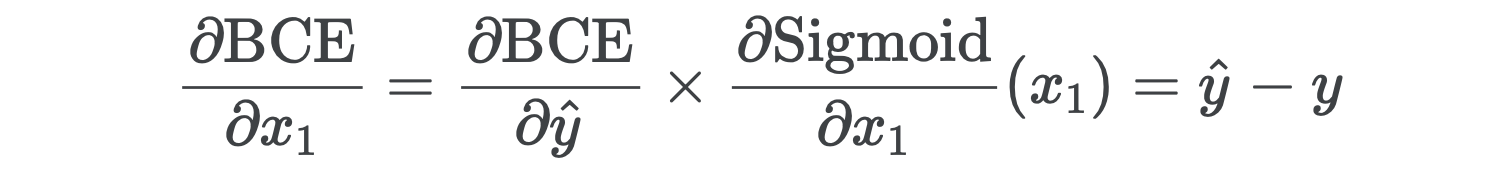
Nice, right? This tells us that the gradient of the loss with respect to the network’s final linear outputs is just the difference between the probabilities y_hat and the labels y. The further apart they are (i.e. the worse our predictions are), the larger the gradient and the larger the update to the weights in the SGD step.

好吧 这告诉我们，损耗相对于网络最终线性输出的梯度就是概率y_hat和标签y之间的差。 它们之间的距离越远(即我们的预测越差)，则梯度越大，SGD步骤中权重的更新就越大。

This is terrific because it means the weights of our network will change gradually as we train and won’t spike or drop suddenly, which would be the case if the gradients were a quadratic or higher-order function of the prediction error. It also demonstrates nicely how a network adjusts its weights based on the error of its predictions.

这太棒了，因为这意味着我们的网络权重将随着训练而逐渐变化，并且不会突然出现尖峰或下降，如果梯度是预测误差的二次函数或更高阶函数，情况就是如此。 它还很好地演示了网络如何根据其预测误差来调整其权重。

In fact, the same is true of multi-classification, where instead of sigmoid we use softmax (or log softmax) as the final activation and cross entropy as the loss. The gradient with respect to the last linear layer’s outputs x is

实际上，多分类也是如此，在这种情况下，我们使用softmax(或对数softmax)代替sigmoid作为最终激活，使用交叉熵作为损失。 相对于最后一个线性层的输出x的梯度为

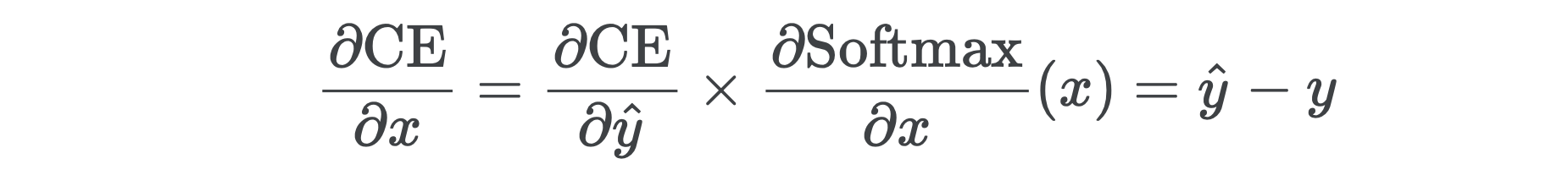
We might cover the multi-class case in more depth in a follow-up post, although it’s more or less the same as what we’ve done so far.

我们可能会在后续文章中更深入地介绍多类案例，尽管它与我们到目前为止所做的大致相同。

线性层 (Linear Layer)

The last component we need to implement is the linear layer, which contains weights and biases. Denoting the linear outputs by z, we have

我们需要实现的最后一个组件是线性层，其中包含权重和偏差。 用z表示线性输出，我们有

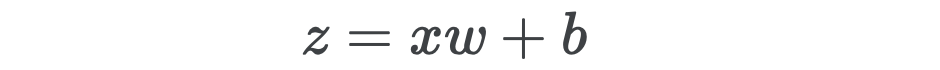
If x is a mini-batch of shape (bs, n_inp), then w has shape (n_inp, 1) and b has shape (1,), with addition being done via broadcasting. To make things easier, for the moment let’s just imagine we have a batch size of one.

如果x是形状(bs, n_inp)的小批量，则w具有形状(n_inp, 1)和b具有形状(1,) ，并且通过广播进行加法(n_inp, 1) 。 为了使事情变得容易，现在让我们假设我们的批处理大小为一个。

There are two gradients to compute this time, one with respect to the weights and another with respect to the bias. To make life easier, let’s write everything out in coordinates.

这次要计算两个梯度，一个相对于权重，另一个相对于偏差。 为了简化生活，让我们将所有内容写成坐标。

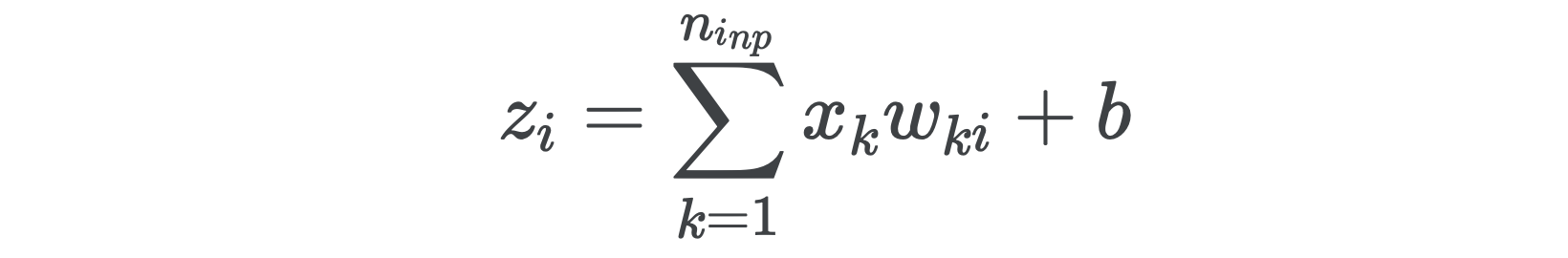
Taking the derivative with respect to the weights, we get

取关于权重的导数，我们得到

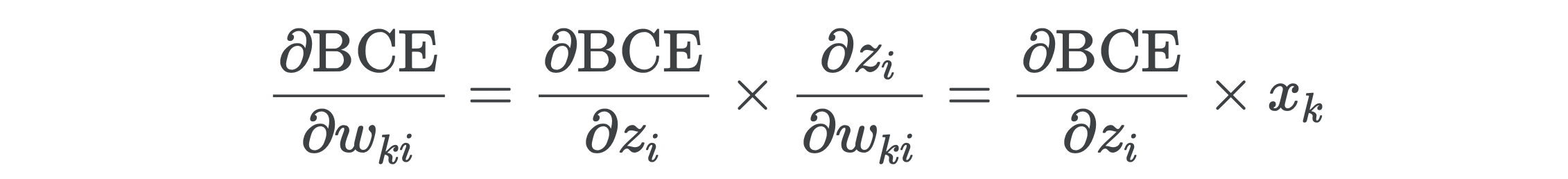
Taking a closer look at these gradients, we see exactly why neural nets are so sensitive to the scale of their inputs. Because the gradients with respect to the weights w are multiplied by the input features x, having features of different magnitudes will result in some gradients being larger than others. These larger gradients will dominate the learning process and prevent the network from learning from all features equally. This is why it’s important to always normalize your data before training.

仔细研究这些梯度，我们可以确切地知道为什么神经网络对输入规模如此敏感。 因为相对于权重w的梯度乘以输入特征x ，所以具有不同幅度的特征将导致某些梯度大于其他梯度。 这些较大的梯度将主导学习过程，并阻止网络平等地学习所有功能。 这就是为什么在训练之前始终对数据进行标准化很重要的原因。

For the derivative with respect to the bias, we have

对于偏见的导数，我们有

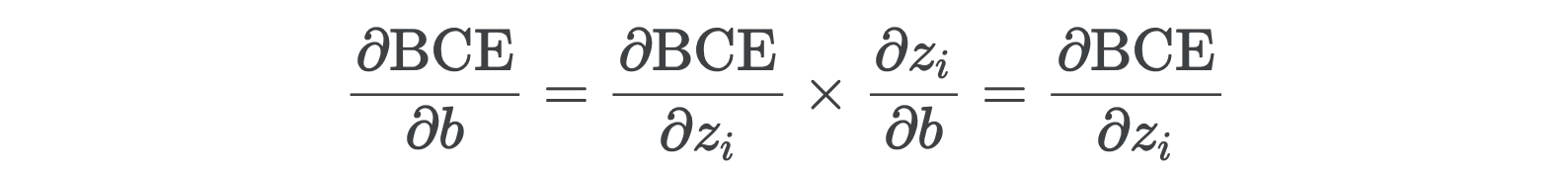
This is nice because we’ll already have the gradient with respect to the linear outputs z stored beforehand in a variable called grad, so we get the gradient with respect to the bias for free, leaving just the weights to deal with. The main obstacle is figuring out how to write the above equations as a matrix product. Whenever I have to do something like this, I just focus on getting the shapes right.

这很好，因为我们已经预先将线性输出z的梯度存储在一个名为grad的变量中，因此我们可以免费获得与偏差有关的梯度，只剩下权重需要处理。 主要的障碍是弄清楚如何将上述方程式写成矩阵乘积。 每当我必须做这样的事情时，我就只专注于正确设置形状。

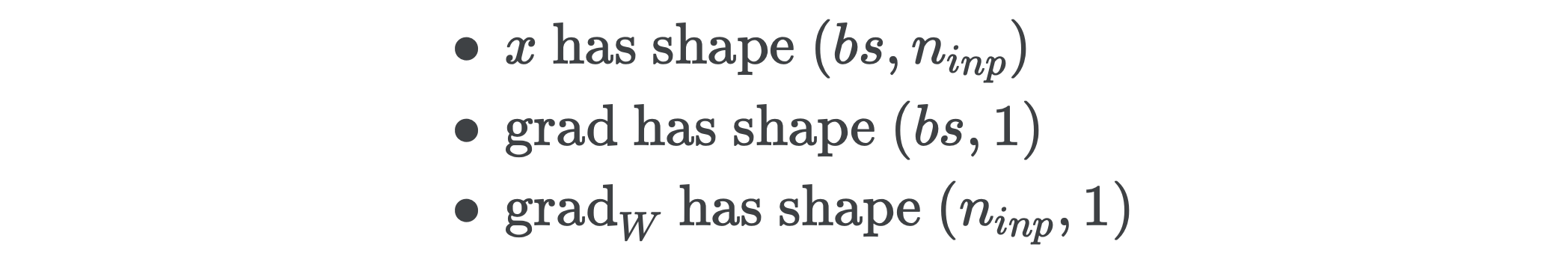
The only way we can multiply x and grad and get something of shape (n_inp, 1) is to re-shape x to have shape (bs, n_inp, 1) and grad to have shape (bs, 1, 1) so that ordinary matrix multiplication over the last two dimensions gives the shape (n_inp, 1). We can do this in numpy be inserting None into an array like x[:, :, None] and grad[:, None, :].

只有这样，我们就可以乘x和grad ，并获得形状的东西(n_inp, 1)是重新塑造x有形状(bs, n_inp, 1)和研究生有形状(bs, 1, 1)使普通最后两个维度上的矩阵乘法给出形状(n_inp, 1) 。 我们可以在numpy通过将None插入到x[:, :, None]和grad[:, None, :] x[:, :, None] grad[:, None, :] x[:, :, None]这样的数组中来实现。

Were there another linear layer we’d also need to compute the gradient with respect to the inputs x so we could keep back-propagating the gradients. This isn’t any more difficult than what we’ve done so far and doing so will allow us to build a network with any number of layers, so let’s go ahead and do it. Since x_k appears in each of activation z_i, the gradient will respect to x_k will involve summing all of the intermediate gradients with respect to z_i.

如果还有另一个线性层，我们还需要计算相对于输入x的梯度，以便可以继续向后传播梯度。 这并没有我们到目前为止所做的任何困难，这样做将使我们能够构建具有任意数量的层的网络，所以让我们继续吧。 由于x_k出现在每个激活z_i ，因此相对于x_k的梯度将涉及求和相对于z_i所有中间梯度。

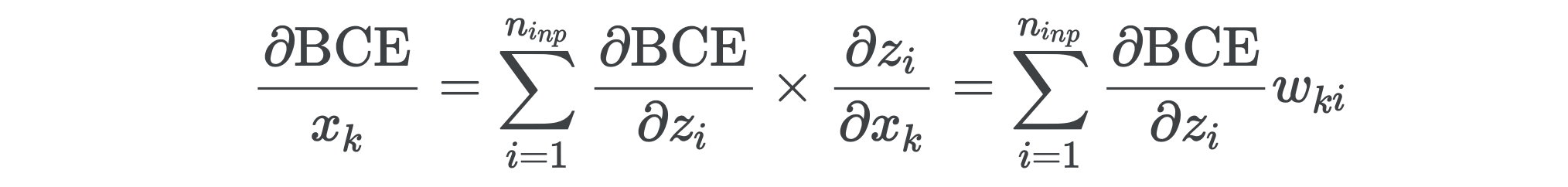
We can re-write this in matrices using the transpose of the weight matrix.

我们可以使用权重矩阵的转置将其重写为矩阵。

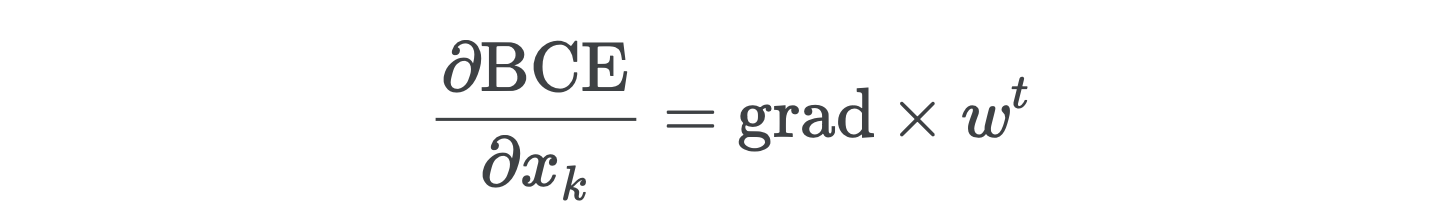
Let’s do a sanity check on the dimensions involved to make sure nothing has gone horribly wrong. Since grad has shape (bs, 1) and w has shape (n_inp, 1), grad × w^t has shape (bs, n_inp), which is exactly the shape of x — just as it should be.

让我们对涉及的维度进行完整性检查，以确保没有出现严重错误。 由于grad的形状为(bs, 1) ，w的形状为(n_inp, 1) ，因此grad × w^t形状为(bs, n_inp) ，正好是x的形状-应当如此。

放在一起 (Putting It All Together)

It’s finally time to string together all of the work we’ve done into a complete network. Then we’ll put it to the test on the breast cancer dataset and see how we compare to sklearn’s built-in logistic model.

现在是时候将我们已经完成的所有工作组合成一个完整的网络了。 然后，将其放在乳腺癌数据集上进行测试，看看如何与sklearn的内置逻辑模型进行比较。

For the optimizer, we’ll stick with vanilla stochastic gradient descent.

对于优化程序，我们将坚持使用香草随机梯度下降法。

培训班 (Trainer Class)

To make life easier, let’s wrap all of the functionality we’ll need to train a network in a single class.

为了使生活更轻松，让我们包装在单个课程中训练网络所需的所有功能。

获取数据 (Getting the Data)

Now let’s grab our data and split off a validation set.

现在，让我们获取我们的数据并分离出一个验证集。

As we saw above, it’s important to always normalize our data before training.

正如我们在上面看到的，在训练之前始终规范化数据很重要。

数据集和数据加载器 (Datasets & Dataloaders)

Since pytorch’s dataset and dataloader classes only work with tensors, we’ll need to implement our own numpy versions in order to train in batches. We’ll omit this for brevity, but you can see the source code at the tinytorch repo.

由于pytorch的数据集和dataloader类仅适用于张量，因此我们需要实现自己的numpy版本以进行批量训练。 为了简洁起见，我们将其省略，但是您可以在tinytorch repo上看到源代码。

训练循环 (Training Loop)

At last we’re finally ready to train our logistic network.

最后，我们终于准备好训练我们的物流网络了。

epoch=  0 | loss= 0.111 | val_loss= 0.106 | val_metric= 0.965
epoch=  1 | loss= 0.108 | val_loss= 0.104 | val_metric= 0.965
epoch=  2 | loss= 0.104 | val_loss= 0.102 | val_metric= 0.974
epoch=  3 | loss= 0.102 | val_loss= 0.100 | val_metric= 0.974
epoch=  4 | loss= 0.099 | val_loss= 0.098 | val_metric= 0.974
epoch=  5 | loss= 0.098 | val_loss= 0.096 | val_metric= 0.982
epoch=  6 | loss= 0.097 | val_loss= 0.095 | val_metric= 0.982
epoch=  7 | loss= 0.095 | val_loss= 0.094 | val_metric= 0.982
epoch=  8 | loss= 0.094 | val_loss= 0.092 | val_metric= 0.982
epoch=  9 | loss= 0.091 | val_loss= 0.091 | val_metric= 0.982

与sklearn的比较 (Comparison with sklearn)

Let’s see how our logistic network stacks up against sklearn’s logistic model.

让我们看看我们的物流网络如何与sklearn的物流模型相结合。

sklearn_model = LogisticRegression(random_state=9)
sklearn_model.fit(X_train, y_train)
sklearn_model.score(X_val, y_val)  0.98245  # We're close!

更深入 (Going Deeper)

Let’s see if we can’t do a bit better using a deeper network. First, we’ll need to implement ReLU for the activations in between our linear layers. ReLU acts as a gate that admits only positive inputs and maps negative inputs to zero.

让我们看看使用更深层的网络是否不能做得更好。 首先，我们需要为线性层之间的激活实施ReLU 。 ReLU充当仅接受正输入并将负输入映射为零的门。

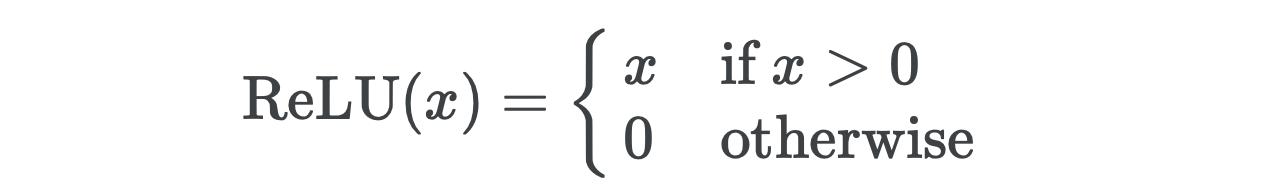
You might recognize its derivative as the Heaviside function, which models an electric current that’s turned on at time t=0.

您可能会认识到其导数为Heaviside函数，该函数对在时间t=0处打开的电流进行建模。

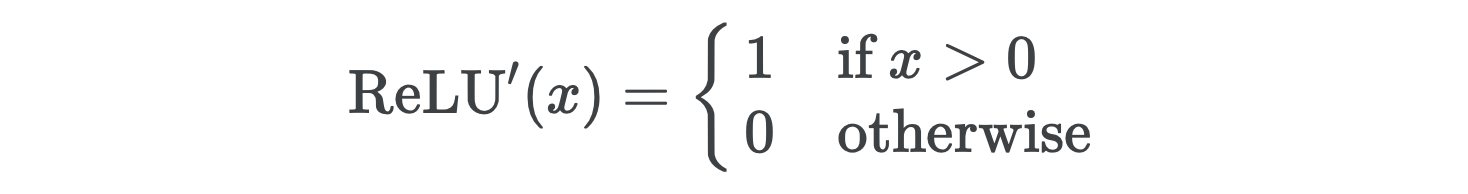
During the backward pass ReLU again acts as a gate that admits gradients corresponding to positive inputs and sends all other gradients to zero.

在反向通过期间， ReLU再次充当门的ReLU ，该门允许对应于正输入的梯度并将所有其他梯度发送为零。

两层网络 (A Two Layer Network)

Now we’re ready to train a multi-layer neural net.

现在我们准备训练多层神经网络。

epoch=  0 | loss= 0.054 | val_loss= 0.076 | val_metric= 0.974
epoch=  1 | loss= 0.052 | val_loss= 0.076 | val_metric= 0.974
epoch=  2 | loss= 0.053 | val_loss= 0.076 | val_metric= 0.974
epoch=  3 | loss= 0.052 | val_loss= 0.076 | val_metric= 0.974
epoch=  4 | loss= 0.052 | val_loss= 0.076 | val_metric= 0.974
epoch=  5 | loss= 0.046 | val_loss= 0.076 | val_metric= 0.974
epoch=  6 | loss= 0.050 | val_loss= 0.076 | val_metric= 0.974
epoch=  7 | loss= 0.051 | val_loss= 0.076 | val_metric= 0.974
epoch=  8 | loss= 0.051 | val_loss= 0.076 | val_metric= 0.982
epoch=  9 | loss= 0.050 | val_loss= 0.076 | val_metric= 0.982

We’re not seeing a clear win with a deeper model, which isn’t all that surprising. For whatever reason, neural nets do not excel at tabular data.

我们没有看到更深层次的模型获得明显的胜利，这并不令人惊讶。 无论出于何种原因，神经网络都不擅长表格数据。

结论 (Conclusion)

That’s about it for us. In this post we were able to build and understand each piece of a feedforward neural net, starting from a single layer logistic network and ending with a multi-layer network. We saw that one reason cross entropy is an effective loss function is that the gradient with respect to the weights depends linearly on the prediction error, which promotes smoother training, and we saw that because the original inputs appear as factors in the network’s gradients it’s essential to always normalize our data before training.

就我们而言。 在这篇文章中，我们能够构建和理解前馈神经网络的每一部分，它从单层逻辑网络开始，到多层网络结束。 我们看到交叉熵是有效损失函数的一个原因是权重的梯度线性依赖于预测误差，从而促进了更平滑的训练，并且我们看到由于原始输入作为网络梯度中的因素而出现，因此必不可少在训练之前总是将我们的数据标准化。

In the next post we’ll turn our attention to convolutional neural nets. To stay up to date with this series of posts and tinytorch, feel free to star the repo or follow me on twitter. Thanks for reading! 🙏

在下一篇文章中，我们将把注意力转向卷积神经网络。 要了解最新的系列帖子和tinytorch ，请随时给回购 tinytorch星标或在Twitter上关注我。 谢谢阅读！ 🙏

翻译自: https://towardsdatascience.com/neural-nets-arent-black-boxes-f0d234e37169