说明文件: (Documentation:)
信息: (Information:)
Source Code: https://github.com/BoostGSoC20/RealIntroductory blog: https://medium.com/@laobelloli/boost-real-9e2dfbfbed5b(Created by Lao Belloli)Mentors: Damian Vicino, Laouen BelloliPartner in GSoC’20: Kishan ShuklaProject Completion: During GSoC’ 20, I completed all work that I got from my proposal to bring Boost.Real to review ready state. I implemented a new and optimized system for integers and rational numbers(integer_number class and real_rational class). I created Taylor expansions for various functions(exp, logarithm, sin, cos, tan, etc). Then used log and exp to make power function. I added several constants required for basic scientific calculations. After combining mine and Kishan Shukla’s work, I hope this library will be ready for review for adding it to boost libraries.Commit History: https://github.com/BoostGSoC20/Real/commits?author=vikram2000bPull Requests: https://github.com/BoostGSoC20/Real/pulls?q=is%3Apr+author%3Avikram2000b
源代码: https : //github.com/BoostGSoC20/Real Introductory博客: https : //medium.com/@laobelloli/boost-real-9e2dfbfbed5b(由Lao Belloli创建) 导师: Damian Vicino,Laouen Belloli GSoC 合作伙伴' 20: Kishan Shukla 项目完成:在GSoC 20期间,我完成了从我的提案中获得的所有工作,以使Boost.Real进入就绪状态。 我为整数和有理数(integer_number类和real_rational类)实现了一个经过优化的新系统。 我为各种函数(exp,对数,sin,cos,tan等)创建了泰勒展开式。 然后使用log和exp使电源起作用。 我添加了一些基本科学计算所需的常数。 将我和Kishan Shukla的工作结合在一起后,我希望该库将准备好进行审核,以便将其添加到增强库中。 提交历史记录: https : //github.com/BoostGSoC20/Real/commits ? author = vikram2000b拉取请求: https : //github.com/BoostGSoC20/Real/pulls? q = is%3Apr+author% 3Avikram2000b
介绍: (Introduction:)
This library aims at providing a data-type that can represent all types of computable real numbers and provides the flexibility of performing arbitrary precision arithmetic, the user can always decide and control the amount precision to be used for a calculation thus controlling the computational power used by the machine.
该库旨在提供一种可以表示所有类型的可计算实数的数据类型,并提供执行任意精度算术的灵活性,用户始终可以决定和控制要用于计算的量精度,从而控制所使用的计算能力由机器。
A number is represented by a program/class x(k) that returns the intervals containing x. Those intervals are sorted from lower to higher precision, the precision of those intervals will increase as we keep on iterating for more precise results. And, we can always decide till the iterations that should be used for the calculation, eventually deciding the maximum precision used by the machine.
一个数字由程序/类x (k)表示,该程序/类返回包含x的间隔。 这些间隔按从低到高的精度排序,随着我们不断迭代以获得更精确的结果,这些间隔的精度将提高。 而且,我们始终可以决定要用于计算的迭代,最终决定机器使用的最大精度。
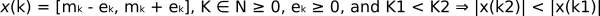
All calculations in this library are done using range arithmetic as every number is represented by an interval. For example, x = 1.2356In decimal base, the intervals will be something like this:First iteration, x = [1, 2]Second iteration, x = [1.2, 1.3]Third iteration, x = [1.23, 1.24]Fourth iteration, x = [1.235, 1.236]Fifth and last iteration, x = [1.2356, 1.2357].Maximum precision is when we can not produce more precise intervals which can represent our number. Here we can not iterate after the fifth iteration, as we have reached maximum precision. The maximum number of iterations can always be customized according to the power of the machine.
该库中的所有计算都使用范围算术完成,因为每个数字都由一个间隔表示。 例如, x = 1.2356,以十进制为基础,时间间隔将类似于以下内容:第一次迭代, x = [1,2]第二次迭代, x = [1.2,1.3]第三次迭代, x = [1.23,1.24]第四次迭代, x = [1.235,1.236]第五次也是最后一次迭代, x = [1.2356,1.2357]。最大精度是当我们无法产生可以表示我们数字的更精确间隔时。 在这里,由于达到了最大精度,因此无法在第五次迭代后进行迭代。 最大迭代次数始终可以根据机器的功率进行定制。
The foundational work was done in GSoC’18 by Lao Belloli and Damian Vicino, then some improvements were done in the library in GSoC’19 by Sagnik Dey and Kimberly Swanson. The link to the blog of everyone’s work is:
基础工作由Lao Belloli和Damian Vicino在GSoC'18中完成,然后由Sagnik Dey和Kimberly Swanson在GSoC'19中的库中进行了一些改进。 每个人的工作博客的链接是:
Laouen Belloli (GSoC’18): https://medium.com/@laobelloli/boost-real-9e2dfbfbed5b
Laouen Belloli(GSoC'18): https ://medium.com/@laobelloli/boost-real-9e2dfbfbed5b
Sagnik Dey (GSoC’19): https://sagnikdey92.github.io/GSoC
Sagnik Dey(GSoC'19): https ://sagnikdey92.github.io/GSoC
Kimberly Swanson (GSoC’19): https://universenox.github.io/gsoc19_Final_Eval
金伯利·斯旺森(GSoC'19): https ://universenox.github.io/gsoc19_Final_Eval
In GSoC’20, I worked with Kishan Shukla. Link of Kishan Shukla’ work:
在GSoC'20中,我与Kishan Shukla合作。 Kishan Shukla的作品链接:
Kishan Shukla (GSoC’20): https://kishanshukla-2307.github.io/posts/2020/08/gsoc-final-evaluation/
Kishan Shukla(GSoC'20): https ://kishanshukla-2307.github.io/posts/2020/08/gsoc-final-evaluation/
This library represents every number using intervals (according to precision) and then do all calculations accordingly. Initially, three data-types were implemented to represent a real number:
该库使用间隔(根据精度)表示每个数字,然后进行相应的所有计算。 最初,实现了三种数据类型来代表实数:
Real Explicit: This is used when the number is a literal, number is written down in code somewhere. It consists of three parts:
实数显式 :当数字是文字,数字在某处的代码中写下来时使用。 它包括三个部分:
(i) vector<T> of digits.
(i)数字的向量<T>。
(ii) A bool specifying sign of the number.
(ii)指定数字符号的布尔符号。
(iii) A decimal point displacement. (exponent)
(iii)小数点位移。 (指数)
Real Algorithm: This data-type is used when a number is represented through a function, it is specially designed for irrational numbers which can be represented by some mathematical function. It consists of three elements:
实算法:当数据通过函数表示时,使用此数据类型,它是专门为可以由某些数学函数表示的非理性数字而设计的。 它包含三个元素:
(i) A function or a lambda function that returns n-th digit of the number.
(i)返回数字的第n位的函数或lambda函数。
(ii) A bool specifying sign of the number.
(ii)指定数字符号的布尔符号。
(iii) A decimal point displacement. (exponent)
(iii)小数点位移。 (指数)
Real Operation: A number that represents an operation between two real numbers. It consists of:
实数运算:一个数字,表示两个实数之间的运算。 它包括:
(i) Two boost::real pointers to its operands.
(i)指向其操作数的两个boost :: real指针。
(ii) An enumerate indicating the type of operation. (+,-,* or /)
(ii)指明操作类型的枚举。 (+,-,*或/)
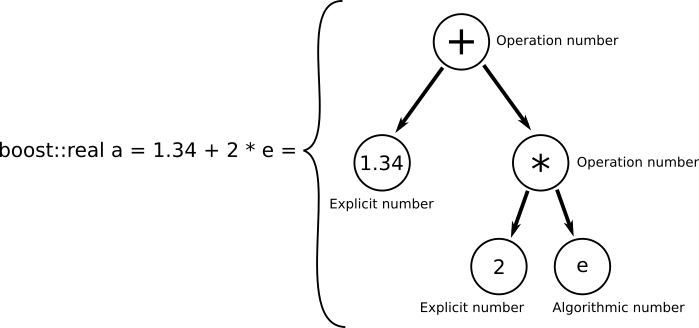
These three representations were used to represent a real number in this library. Every operation between two real numbers was represented by a real_operation number, and a real_operation number was a tree pointing to its operands and storing the type of operations it is associated with. Laouen implemented all these types and led the foundation of this library, detailed information on working and implementation of these types can be found at the blog written by Laouen. After that, in GSoC’19, a lot of improvements were done and a basic division algorithm was implemented. A new base was tried and implemented but it was not stable at the time. A back-end class exact_number was created which represents a finite real number, it is used as a back-end number to represent bounds of the interval which represents our real number according to precision and later real_explicit was also modified to store a number in an exact_number, so the members real_explicit class were not a vector, exponent, and bool, it was simply an exact_number which stores a vector, exponent, and bool to represent a finite real number.
这三个表示用来表示该库中的实数。 两个实数之间的每个运算都由一个real_operation数表示,而real_operation数是指向其操作数并存储与之关联的运算类型的树。 Laouen实现了所有这些类型并领导了此库的基础,有关这些类型的工作和实现的详细信息可以在Laouen撰写的博客中找到。 之后,在GSoC'19中进行了许多改进,并实现了基本的划分算法。 尝试并实施了新的基础,但当时还不稳定。 创建了一个后端类Precision_number ,它表示有限的实数,它用作后端数字来表示区间的边界,该区间的边界根据精度代表了我们的实数,后来real_explicit也被修改为将数字存储在precision_number ,因此成员real_explicit类不是向量,指数和布尔,它只是一个精确的数字 ,用于存储向量,指数和bool来表示有限的实数。
After all work done on this library for two years, some improvements were needed to make it ready for the final review. Division and multiplication algorithms were needed to be improved, stable implementation of a larger base was needed, and several more mathematical functionalities were needed to make it more promising. My proposal had the following ideas:
在对该库进行了两年的所有工作之后,需要进行一些改进以使其准备好进行最终审核。 需要改进除法和乘法算法,需要稳定实现更大的基数,还需要更多的数学功能以使其更有希望。 我的建议有以下想法:
- Implementing a base of 2^n, where n is the number of bits of the variable whose vector will be used to represent the number. 实现一个2 ^ n的基数,其中n是变量的位数,其矢量将用于表示该位数。
- A separate system for integer and rational number, which will not have a tree structure for operation between an integer and a rational number. 一个单独的整数和有理数系统,它将没有树结构在整数和有理数之间进行运算。
- Implement an integer power method for real numbers. 为实数实现整数幂方法。
- Factorial method for integer numbers. (Useful for Taylor expansions). 整数的阶乘方法。 (对于泰勒展开有用)。
- Implementing some mathematical functions using Taylor Expansions. (exponential, logarithm, and trigonometric functions.) 使用泰勒展开式实现一些数学函数。 (指数,对数和三角函数。)
- Implementing the Real^Real method, using logarithm and exponential functions. 使用对数和指数函数实现Real ^ Real方法。
- Implementing an algorithm for Pi. (Chudnovsky Algorithm.) 为Pi实现算法。 (Chudnovsky算法。)
- Adding some constants to the library. 在库中添加一些常量。
Two students were selected to work on this library, me and Kishan Shukla. Although our ideas were independent, there was a huge overlap of ideas in our proposals. So, a lot of work was divided between us. After the division of work, I was left with the following tasks.
我和Kishan Shukla被选为该图书馆的两名学生。 尽管我们的想法是独立的,但我们的提案中有很多想法重叠。 因此,我们之间的工作很多。 分工之后,我剩下了以下任务。
- Deciding and implementing a stable and efficient base system. This task was for both of us, me and Kishan, and we planned to complete it during the community bonding period. 决定并实施一个稳定而有效的基础系统。 这个任务是给我们我和Kishan的,我们计划在社区联系期间完成它。
- Implement a digit by digit base conversion method for real::algorithm number. (This was implemented during the community bonding period.) 实现实数::算法数的逐位基数转换方法。 (这是在社区联系期间实施的。)
- Introduce integers and rationals as special cases of real number for better optimization possibilities. 将整数和有理数作为实数的特殊情况引入,以实现更好的优化可能性。
- Implement a factorial method for integers. 为整数实现阶乘方法。
- Implement Taylor expansions. 实施泰勒展开式。
- Implement real^real function. 实现真实的真实功能。
- Add proposed constants. 添加建议的常量。
During community boding, we decided and implemented a stable and efficient base. We agreed on implementing a base of (std::numerical_limits<T>::max()/4)*2 + 1, where T is the type of integral data used to store numbers. (Like int, long, etc).
在社区讨论过程中,我们决定并实施了一个稳定而有效的基础。 我们同意实现(std :: numerical_limits <T> :: max()/ 4)* 2 + 1的基数,其中T是用于存储数字的整数数据的类型。 (如int,long等)。
Then I implemented a digit by digit base conversion method for real::algorithm numbers. Currently, that function is stored as a convenience function, which can be to convert the base of real::algorithm number.
然后,我对real :: algorithm数字实现了逐位基数转换方法。 当前,该函数存储为便捷函数,可以转换为实数::算法数的基数。
GSoC阶段1: (GSoC Phase 1:)
Main Goals:
主要目标:
- Documentation for digit by digit base conversion method. 逐位基数转换方法的文档。
- Implement the proposed system for integer and rational numbers. 实现建议的整数和有理数系统。
- Make tests and documentation for the above system. 对上述系统进行测试和记录。
Digit by digit base conversion:
逐位数字转换:
This function was added to help when function (for real_operation number) available to the user gives a number that is represented in a different base than internal base representation. For example, if the base of the number that is represented by function is decimal then this function can be used to create another wrapper which will do digit by digit base conversion and return that number in required base.
当用户可用的函数(用于real_operation编号)给出的数字以与内部基本表示形式不同的基本形式表示时,添加了此功能以提供帮助。 例如,如果该函数表示的数字的底数是十进制,则可以使用此函数创建另一个包装器,该包装器将逐位进行底数转换并以所需的底数返回该数字。
The function was implemented by representing a digit addition as a multiplication and addition operation. Just assume there is a number N represented in base B1 as N1 and in base B2 as N2(the value of both N1 and N2 are the same, but they are represented in different base). Now, if we append a digit to this number N1 (in base B1), and now we want to produce an equivalent change in N2 (which is stored in base B2), and we are not allowed to do the whole base conversion, we need to do that using N2, both bases B1 and B2, and value of digit that was added in base B1.
通过将数字加法表示为乘法和加法运算来实现该功能。 只需假设在基数B1中将数字N表示为N1,在基数B2中将数字N表示为N2(N1和N2的值相同,但是它们以不同的基数表示)。 现在,如果我们在此数字N1后面附加一个数字(在基数B1中),现在我们想在N2中产生一个等效的变化(存储在基数B2中),并且不允许进行整个基数转换,需要使用N2,基数B1和B2以及在基数B1中添加的数字值来执行此操作。
N1 = a1a2a3…..an (a1 -> first digit, a2->second digit,…..)N2 = b1b2b3…..bn(b1-> first digit, a2->second digit,……)here N1 = N2, but the base of both numbers are different, B1 and B2 respectively. Now we append a digit a(n+1) in N1, what change should we make in N2, to make N2 = N1?Now, appending digit a(n+1) is equivalent to :N1 = N1*B1 + a(n+1).So, we will make the same change in N2:N2 = N2*B1 + a(n+1)And that will give us the result of adding a digit in a different base.
N1 = a1a2a3 ..... an(a1->第一位数字,a2->第二位数字,.....)N2 = b1b2b3 ..... bn(b1->第一位数字,a2->第二位数字,……)这里N1 = N2,但两个数字的基数分别为B1和B2。 现在我们在N1后面加上一个数字a(n + 1),我们应该在N2上做些什么变化才能使N2 = N1?现在,在后面加上数字a(n + 1)等于:N1 = N1 * B1 + a( n + 1)。因此,我们将在N2中进行相同的更改:N2 = N2 * B1 + a(n + 1),这将为我们提供在不同基数中添加数字的结果。
Link to initial commit of convenience function: https://github.com/BoostGSoC20/Real/commit/961257de476e5de99fe195c5c2f5f17807b43aa6 (Later the name of the function was modified to append_digit from add_digit).
链接到便利功能的初始提交: https : //github.com/BoostGSoC20/Real/commit/961257de476e5de99fe195c5c2f5f17807b43aa6 (此后功能名称已从add_digit修改为append_digit)。
Integer and rational numbers:
整数和有理数:
Every operation we do in this library is represented by real_algorithm, which points to numbers on which operation is done and the type of operation which needs to be done. Internally a new copy of operands will be generated and operation will point to those copies. Now, sometimes for small and repetitive operations, the user may not want to create extra copies and a complex tree of operations. Now, a special system for integer and rational number was proposed to avoid these operation trees, any operation involving an integer type and a rational type number will create an integer or rational type number, all other operations like real_explicit + real_rational will create an operation tree. So, they provide some optimization scopes for users.
我们在该库中执行的每个操作均由real_algorithm表示,该指针指向要执行的操作的编号以及需要执行的操作的类型。 内部将生成一个新的操作数副本,并且操作将指向这些副本。 现在,有时对于小的重复性操作,用户可能不想创建额外的副本和复杂的操作树。 现在,为避免这些运算树,提出了一种特殊的整数和有理数系统,任何涉及整数类型和有理类型数的运算都将创建整数或有理类型数,所有其他运算(如real_explicit + real_rational都将创建运算树) 。 因此,它们为用户提供了一些优化范围。
A class “integer_number” was added to store integer type numbers and another class “real_rational” which stores two “integer_number” objects to represent a rational number in form of “a/b”, where a and b are integers, was added. Initially, integers type numbers were stored by “integer_number” class, and rational numbers were stored by “real_rational” class, later it was decided to use integer_number only in the back-end, to support real_rational class. Then integer numbers(defined by the user) were also represented by real_rational class(in form of a/1). This shifting was done to provide better maintenance of code.
添加了一个类“ integer_number”来存储整数类型数字,并添加了另一个类“ real_rational”来存储两个“ integer_number”对象以“ a / b”的形式表示一个有理数,其中a和b是整数。 最初,整数类型数字由“ integer_number”类存储,有理数则由“ real_rational”类存储,后来决定仅在后端使用integer_number来支持real_rational类。 然后,整数(由用户定义)也由real_rational类(以a / 1的形式)表示。 进行此更改是为了更好地维护代码。
Later, tests for these classes were designed.
后来,设计了这些类的测试。
GSoC阶段2: (GSoC Phase 2:)
Main Goals:
主要目标:
- Implement a factorial method for integers. 为整数实现阶乘方法。
- Implement Taylor expansions of exponent, logarithm, sin, cos, tan, sec, co-sec, and cot functions. 实现指数,对数,sin,cos,tan,sec,co-sec和cot函数的泰勒展开。
Factorial:
阶乘:
The main reason behind implementing factorial function was to implement Taylor expansion. We need factorials for Taylor expansions.The factorial of a number is calculated through repeated multiplication. But after some discussion, this function was not merged into the library. Because, in Taylor expansion, calculating factorial by using factorial of the previous number was more efficient. So, using this function was inefficient, because it calculates every factorial from start. And only use of this function was to help in Taylor expansion, and it was not used in those calculations. So, this function was not added.The factorial function will calculate factorial of N like this: n! = 1×2×3×…..×nbut if we have (n-1)! then:n! = n × (n-1)!In the calculation of Taylor expansions, we need to calculate (n-1)! or (n-2)! before n! so keeping those factorials and just using them again is better instead of calculating it again from start.
实现阶乘函数的主要原因是实现泰勒展开。 对于泰勒展开式,我们需要阶乘。一个数的阶乘是通过重复乘法来计算的。 但是经过一番讨论,此功能并未合并到库中。 因为在泰勒展开式中,使用先前数字的阶乘计算阶乘更为有效。 因此,使用此函数效率不高,因为它从一开始就计算每个阶乘。 而且仅使用此功能有助于泰勒展开,而在这些计算中未使用它。 因此,未添加此函数。阶乘函数将像这样计算N的阶乘:n! = 1×2×3×…..×n但是如果我们有(n-1)! 然后:n! = n×(n-1)!在泰勒展开式的计算中,我们需要计算(n-1)! 或(n-2)! 在n之前! 因此保留这些阶乘并再次使用它们比从头开始进行计算更好。
Taylor Expansion:
泰勒扩展:
A Taylor expansion is an infinite converging series, which can represent a continuous and differentiable function, more information can be found on this Wikipedia page.The pseudo-code of the exponential function:
泰勒展开式是一个无限收敛的级数,可以表示一个连续的可微函数,可以在此Wikipedia页面上找到更多信息。指数函数的伪代码为:
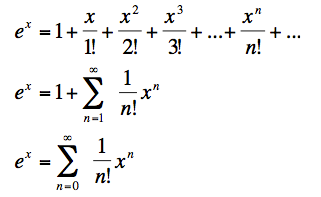
/**
* EXPONENT FUNCTION USING TAYLOR EXPANSION
* @brief: calculates exponent of a exact_number using Taylor expansion
* @param: num: the number. whose exponent is to be found
* @param: max_error_exponent: Absolute Error in the result should be < 1*base^(-max_error_exponent)* @author: Vikram Singh Chundawat
**/// I am using double here to represent our numbers, but in library exact_number was used, and actual function is a bit different than this. This code is to just explain working of exp function.double exponent(double num, size_t max_error_exponent){double result = 1;
int term_number = 1;
long long factorial = 1;
int cur_term = 0;
double max_error = power((double)1, -max_error_exponent);
double x_pow = 1;
do{
result += cur_term;
factorial *= term_number;
++term_number;
x_pow *= num;
cur_term = x_pow/factorial;
}while(abs(cur_term) > max_error);return result;
}Four Taylor expansion functions were implemented: exp, ln, sin, and cos. Also, I implemented other trigonometric functions that could be calculated using combinations of these.
实现了四个泰勒展开函数:exp,ln,sin和cos。 另外,我实现了其他三角函数,可以使用这些函数的组合来计算。
Minima and Maxima
极小值和千里马
The above function is to calculate the exp of a single exact number. But in intervals, we need to check for points of local minima and maxima to show correct results.
上面的功能是计算单个精确数字的exp。 但是在间隔中,我们需要检查局部最小值和最大值的点以显示正确的结果。
Logarithm and exponent do not have local maxima-minima, and they are always increasing function, so exp([a, b]) = [exp(a), exp(b)] and ln([a, b]) = [ln(a), ln(b)].But trigonometric functions are different. Look at the graph of sin(x):
对数和指数没有局部最大值-最小值,并且它们始终是递增函数,因此exp([a,b])= [exp(a),exp(b)]和ln([a,b])= [ ln(a),ln(b)]。但是三角函数是不同的。 看一下sin(x)的图:
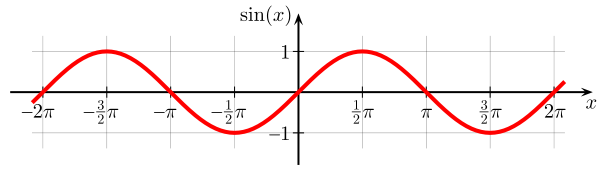
If the input interval [0,π], then it means, our result can be anywhere between 0 and 1. So, the output interval should be [0,1]. But if we directly calculate values of lower and upper bound of input interval, then sin(0) = 0 and sin(π) = 0, then output will be [0,0]. In such cases, where there exists minima or maxima of function between upper and lower bound of input, direct values of the function at upper and lower bound of input interval will give us output which will not contain the correct answer, it will give us wrong output interval.
如果输入间隔为[0,π],则意味着我们的结果可以在0到1之间。因此,输出间隔应该为[0,1]。 但是,如果我们直接计算输入间隔的上下限值,则sin(0)= 0且sin(π)= 0,则输出将为[0,0]。 在这种情况下,如果输入上下限之间存在函数的最小值或最大值,则函数在输入间隔上下限处的直接值将给我们输出不包含正确答案的输出,这将给我们带来错误输出间隔。
Trigonometric functions have intervals of 2π, so there can exist a point of minima and maxima between upper and lower bound of input interval, so we need to check for those points. One way would be to check for multiples of π and π/2 in input interval, but Pi is an irrational number, and checking for its multiples is too inefficient. The first derivative of the function is zero on point of minima and maxima, and it changes its sign at those points. So, points of minima and maxima can be checked using derivatives of functions, we can check whether the sign of derivative is changing or not in input interval. And, we can calculate the derivative of a trigonometric function is also a trigonometric function and we can calculate all trigonometric functions using a combination of sin and cos. So, a function that can calculate both sin and cos in one go was created, it is more efficient than the separate calculation of both functions. Here is the pseudo-code of sin_cos function:
三角函数的间隔为2π,因此在输入间隔的上限和下限之间可能存在一个最小值和最大值的点,因此我们需要检查这些点。 一种方法是检查输入间隔中的π和π/ 2的倍数,但是Pi是一个无理数,并且检查其倍数效率太低。 函数的一阶导数在最大值和最小值处为零,并且在这些点处更改其符号。 因此,可以使用函数的导数检查最小值和最大值的点,我们可以检查输入间隔中导数的符号是否在变化。 并且,我们可以计算三角函数的导数也是三角函数,并且可以使用sin和cos的组合来计算所有三角函数。 因此,创建了一个可以一次性计算正弦和余弦的函数,它比分别计算两个函数的效率更高。 这是sin_cos函数的伪代码:
/**
* SINE AND COSINE FUNCTION USING TAYLOR EXPANSION
* @brief: calculates cos(x) and sin(x) of a exact_number using Taylor expansion
* @param: x: the number representing angle in radian
* @param: max_error_exponent: Absolute Error in the result should be < 1*base^(-max_error_exponent)
* @param: upper: if true: error lies in [0, +epsilon]
* else: error lies in [-epsilon, 0], here epsilon = 1*base^(-max_error_exponent)
* @return: a tuple containing sin(x) and cos(x)
* @author: Vikram Singh Chundawat
**/// I am using double here to represent our numbers, but in library exact_number was used, and actual function is a bit different than this. This code is to just explain working of exp function.std::tuple<double, double> sin_cos(double x, size_t max_error_exponent){double sin_result("0");
double cos_result("0");
double cur_sin_term = x;
double cur_cos_term("1");
double cur_power = x;
long long factorial("1");
long long factorial_number("1");
unsigned int term_number_int = 0;
double max_error = pow((double)1, -max_error_exponent);
do{if(term_number_int % 2 == 0){
sin_result += cur_sin_term;
cos_result += cur_cos_term;
}
else{
sin_result -= cur_sin_term;
cos_result -= cur_cos_term;
}
++term_number_int;
factorial_number = factorial_number + literals::one_exact<T>;
factorial *= factorial_number;
cur_power *= x;
cur_cos_term = cur_power/factorial;++factorial_number;
factorial *= factorial_number;
cur_power *= x;
cur_sin_term = cur_power;
cur_sin_term/factorial
}while( (abs(cur_cos_term) > max_error) || (cur_sin_term) > max_error );return std::make_tuple(sin_result, cos_result);
}Using this function, we can calculate all trigonometric functions, so derivatives can be easily calculated and we can check for points of minima and maxima, and can give results accordingly.
使用此函数,我们可以计算所有三角函数,因此可以轻松计算导数,并且可以检查最小值和最大值的点,并可以给出相应的结果。
Still, simply using derivatives for maxima-minima points may lead us to the wrong answer. Just consider the input [(-π/2) + e, (3π/2) +e](e is very small value) and we want to calculate sin(x) for this interval. First, we will check for sign of derivative, which is cos(x), the sign of cos(x) will be same at both upper and lower bounds of input interval, so our system will say no maxima-minima points so the result we will be something like [-0.99, -0.98]. If we look carefully at the graph of sin(x), there are both maxima and minima between the upper and lower bound of this input, so our system should give [-1, 1].
但是,仅对最大最小值点使用导数可能会导致我们得出错误的答案。 只需考虑输入[[--π/ 2)+ e,(3π/ 2)+ e](e是很小的值),我们就想为此间隔计算sin(x)。 首先,我们将检查导数的符号,即cos(x),cos(x)的符号在输入区间的上下边界都相同,因此我们的系统将说没有最大值-最小值点,因此结果我们将是[-0.99,-0.98]。 如果仔细查看sin(x)的图,则此输入的上限和下限之间都存在最大值和最小值,因此我们的系统应给出[-1,1]。
The reason for such checking is that a minima-maxima point always alters the sign of derivative. So, the two maxima-minima points will alter the sign of the system two times, so in the end, there will be no change in sign of derivative.
进行这种检查的原因是,最大极小点总是会改变导数的符号。 因此,两个最大-最小点将两次更改系统的符号,因此最后,导数的符号将不会发生变化。
Initially, the system was implemented just like previously proposed, we just checked sign of derivative, later in the third phase we realized this will be wrong and we agreed to make some proper and detailed checks. First, we classified our input between these three categories.
最初,该系统的实现方式与之前建议的一样,我们只是检查了派生符号,后来在第三阶段中我们意识到这是错误的,我们同意进行一些适当而详细的检查。 首先,我们将我们的输入分类为这三个类别。
- Upper bound — lower bound < 4. 上限-下限<4。
- 4 ≤ Upper bound — Lower Bound <8. 4≤上限-下界<8。
- Upper bound — Lower bound ≥8. 上限—下限≥8。
Someone may wonder why didn’t we use multiples of π for such checking, the reason was the inefficiency of the algorithm used to generate π. This simple check will make this function too slow so we used 4 instead. I am writing here the pseudo-code of the algorithm used to calculate sin(x), which will make things more clear and easy to understand and I am also explaining everything in comments of code. Please go through it:
有人可能想知道为什么我们不使用π的倍数进行这种检查,原因是用于生成π的算法效率低下。 这个简单的检查会使此功能太慢,因此我们改用4。 我在这里编写用于计算sin(x)的算法的伪代码,这将使事情变得更清晰和易于理解,并且我还将解释代码注释中的所有内容。 请检查一下:
auto [sin_lower, cos_lower] = sin_cos(lower_bound);
auto [sin_upper, cos_upper] = sin_cos(upper_bound);
/**
First we ensure that our input interval is greater than 2π or not. We can either check that by comparing the difference of upper and lower bound with 2π or a number greater than 2π. We will check whether the difference is greater than 8 or not. If the difference is greater than 8 then we are sure that difference is greater than 2π. We are not using π here for checking because algorithm for π is very complex and checking with that number will be very inefficient. The condition of difference between 2π and 8 will be checked in next case. Here we will only check whether our number is greater than 8 or not. If it is, then we will give hard-coded output of [-1, 1] because the result can be anything between -1 to 1.
**/
if(upper_bound - lower_bound >= 8){
result.lower_bound = -1;
result.upper_bound = 1;
}
/**
Now we will check whether the difference is greater than 4 or not.
4 is greater than π, so we are sure that there is at least one minima/maxima. But there can exist both minima and maxima, as input can be anywhere between [4,8). So, we will check sign of derivative of sin, which is cos. If there is one or three minima/maxima, sign of derivative will change once, so we will different signs of derivative on upper and lower bound. If there are both minima and maxima, sign of derivative will change twice, so at the end, sign of derivative in both upper and lower bound will remain same.
**/
else if(upper_bound - lower_bound >= 4){
/**
If sign of derivative, which is cos(x), if it is same for both upper and lower bound. Then we will return hard-coded output [-1, 1]. Because we are sure that there is at least one minima-maxima, if sign does not changes then it simply means there were both maxima and minima.
**/
if(cos_upper.positive == cos_lower.positive){
result.lower_bound = -1;
result.upper_bound = 1;
}
/**
Now, the sign was changed, then there is either one minima/maxima or three maxima minima. There can exist either one minima/maxima or three points of maxima. In case of three points of maxima, and difference between inputs less than 8, both ends of sin will have same sign and sin(x) of mid point of upper and lower bound will have opposite sign from end points. In that case, we will give hard coded output [-1, 1].
**/
else{
auto mid = (upper_bound + lower_bound) / 2;
if(sin_lower.positive == sin_upper.positive && sine(mid).positive == sin_upper.positive){
result.lower_bound = -1;
result.upper_bound = 1;
}
/**
We will check sign of lower bound of derivative, if it is positive, then initially function was increasing then it would have gone up to 1 and then started decresing. So, the output will be [min(sin(upper_bound, sin(lower_bounf))), 1].
**/
else if(cos_lower.positive){
result.lower_bound = min(sin_upper, sin_lower);
result.upper_bound = 1;
}/**
Now if the sign of derivaye is negative, then initially function was decreasing. So, the function would have got to -1 and then again started incresing. So, the output should be [-1, max(sin_lower, cos_lower)]
**/
else{
result.lower_bound = -1;
result.upper_bound = max(sin_upper, sin_lower);
}
}
}
/**
Now, the final case, the difference is less than 4. There are two possibilities, no maxima/minima or one maxima/minima. If sign of derivative changes, then one maxima/minima, if it doesn't, then no maxima/minima.
**/
else{
/**
If sign does not changes, then no maxima/minima or both maxima and minima. We will check sign of derivative at mid of interval, if it is not same as that of lower and upper bounds. Then we have both maxima and minima.
**/
if(cos_upper.positive == cos_lower.positive){
/* if sign of derivative at mid point is not same as at end points then both minima and maxima are there
*/
auto mid = (upper_bound + lower_bound)/2;
if(cos(mid).positive != cos_lower.positive){
result.lower_bound = -1;
result.upper_bound = 1;
}
/* If cos(x), which is derivative of sin(x), is positive, then function was increasing in that interval. So, the output will be [sin_lower, sin_upper].
*/
else if(cos_lower.positive){
result.lower_bound = sin_lower;
result.upper_bound = sin_upper;
}
/* If it is negative, then function was decreasing in that interval. SO, the output will be [sin_upper, sin_lower].
*/
else{
result.lower_bound = sin_upper;
result.upper_bound = sin_lower;
}
}
/**
If sign changes, then one maxima/minima. So, we will check sign of derivative at lower bound of input. If it is positive, then function was increasing initially. So, the output will be [min(sin_lower, sin_upper), 1]. If it is negative, then function was decreasing initially. So, the output will be [-1, max(sin_upper, sin_lower)].
**/
else{
if(cos_lower.positive){
result.lower_bound = min(sin_lower, sin_upper);
result.upper_bound = 1;
}
else{
result.lower_bound = -1;
result.upper_bound = max(sin_lower, sin_upper);
}
}
}Theoretically the minima and maxima for all trigonometric functions other than sin and cos are-inf and +inf, we did not have any representation for infinite values and also, returning an interval like [-inf, +inf], does not make sense.
从理论上讲,除sin和cos are-inf和+ inf外的所有三角函数的最小值和最大值,我们没有任何表示无限值的方法,并且返回[-inf,+ inf]之类的区间也没有意义。
So instead of returning any results, we modified the code to keep iterating for more accurate interval until we get an interval which does not contain any minima or maxima point. If maximum precision is reached and we still don’t get such interval, we throw an error. Pseudo Code for calculation of tan(x) is shown below:
因此,我们没有返回任何结果,而是修改了代码以使迭代保持更准确的间隔,直到获得不包含任何最小值或最大值点的间隔为止。 如果达到最大精度,但我们仍然没有得到这样的间隔,则会抛出错误。 计算tan(x)的伪代码如下所示:
// we will keep on iterating until we get our interval in domain of tan(x)
while(true)
{
auto [sin_lower_tmp, cos_lower_tmp] = sin_cos(input.lower_bound);
auto [sin_upper_tmp, cos_upper_tmp] = sin_cos(input.upper_bound);
bool iterate_again;
if(input.upper_bound - input.lower_bound >= literals::4){
iterate_again = true;
}
else{
/**
Now if difference between lower and upper bounds of interval is less than 4, then there can exist 0,1 or 2 minima/maxima points. First we will check whether the sign of cos(x) from lower to upper bound is changed or not, if it is, then we have one point of maxima/minima. Then we will iterate for better input.
**/
if(cos_upper_tmp.positive != cos_lower.positive || cos_lower_tmp == 0 || cos_upper_tmp == 0){
iterate_again = true;
}
/**
Now, if sign is not changed, then we will check if sign of mid point of derivative is same as end points. If it is, then no points of minima/maxima, no need to iterate further.
**/
else{
auto mid = (input.lower_bound + input.upper_bound ) / 2;
if(cos(mid).positive != cos_lower_tmp.positive){
iterate_again = true;
}
else{
iterate_again = false;
}
}
}
// if we have point of maxima of minima in our input interval
if(iterate_again){
// updating the boundaries of lhs
if(_precision >= input.maximum_precision()){
throw max_precision_for_trigonometric_function_error();
}
input.iterate_n_times(1);
++_precision;
}
else{
sin_lower = sin_lower_tmp;
sin_upper = sin_upper_tmp;
cos_lower = cos_lower_tmp;
cos_upper = cos_upper_tmp;
break;
}
}result.lower_bound = sin_lower / cos_lower;
result.upper_bound = sin_upper / cos_upper;
break;The logarithm function is not defined for non-positive numbers and sometimes our input can have an interval whose lower bound is negative or zero and upper bound is positive. Then we will iterate for more accurate intervals and show results if the whole interval turns out to be positive else throw an error.
未为非正数定义对数函数,有时我们的输入可以有一个下限为负或零且上限为正的区间。 然后,我们将迭代一个更准确的时间间隔,并在整个时间间隔为正数时显示结果,否则将引发错误。
GSoC阶段3: (GSoC Phase 3:)
Main Goals:
主要目标:
- Implement real^real operation(power operation), using exp and log function. 使用exp和log函数实现真实^真实操作(电源操作)。
- Define some commonly used scientific constants. 定义一些常用的科学常数。
- Implement tests. 实施测试。
- Document the work. 记录工作。
Real^Real:
真实^真实:
The general syntax of a^b can be evaluated using a^b = exp(b * log(a)). We will use the same idea to find non-integral powers of real numbers, integral powers will be calculated using the integer power method created by Kishan Shukla.
可以使用a ^ b = exp(b * log(a))来评估a ^ b的常规语法。 我们将使用相同的思想来找到实数的非整数幂,将使用Kishan Shukla创建的整数幂方法来计算整数幂。
Non-integral Powers of negative numbers:
负数的非整数幂:
Non-integral powers of negative numbers is a complex number. Its representation is of form (a+ib) form. More information can be found here. Currently, our library does not support imaginary numbers, so we throw an error for such inputs.Here is the code for power function:
负数的非整数幂是一个复数。 其表示形式为(a + ib)形式。 在这里可以找到更多信息。 当前,我们的库不支持虚数,因此我们对此类输入抛出错误,这是幂函数的代码:
power(real_num, power){
// checking whether the number is integer or not
try{
result = real(real_operation<T>(real_num, power, OPERATION::INTEGER_POWER));
return result;
}
catch(const negative_integers_not_supported& e1){
power *= -1;
result = real(real_operation<T>(real_num, power, OPERATION::INTEGER_POWER));
result = real(real_operation<T>(one, result, OPERATION::DIVISION));
return result;
}
catch(const non_integral_exponent_exception& e2){
try{
/**
* result = exp(exponent * log(real_num))
* Warning: the result of non-integral power of a negative number is a complex number, and we do not support complex numbers. So, that will generate error.
* Note: The error will be generated by logarithm function.
**/
/**
* Now, if number is negative, then logarithm function will check out and throw error
**/
result = real(real_operation<T>(real_num, zero, OPERATION::LOGARITHM));
result = real(real_operation<T>(result, power, OPERATION::MULTIPLICATION));
result = real(real_operation<T>(result, zero, OPERATION::EXPONENT));
return result;
}
catch(const logarithm_not_defined_for_non_positive_number& e3){
throw non_integral_power_of_negative_number();
}
}
}Scientific constants:Some common constants like mass and charge of subatomic particles were added. The values were taken from the most accurate measurements available.
科学常数:添加了一些常见常数,例如亚原子粒子的质量和电荷。 该值取自最精确的测量值。
Square root function:Although this function was not in my proposal, but I was left with some time in the end. So I added this function to the library. This function simply calculates x^(1/2) using logarithm and exponent function.
平方根函数:尽管此函数不在我的建议中,但最后我还剩下一些时间。 因此,我将此功能添加到库中。 该函数使用对数和指数函数简单地计算x ^(1/2)。
After that, all remaining tests were made and some minor bugs which were detected at the time of testing were fixed. After that, this report was written along with some documentation in code.
之后,进行所有剩余的测试,并修复了在测试时检测到的一些小错误。 之后,此报告与一些代码文档一起编写。
Doxygen documentation will be automatically generated from comments written in code.
Doxygen文档将通过代码注释自动生成。
This entire project was a very good journey and we learned a lot during this period, and also understood a lot of standard practice that is followed by programmers when dealing with big projects. Special thanks to mentors Damian Vicino and Laouen Belloli. They constantly gave us feedback on our work and taught us a lot.
整个项目是一段非常好的旅程,我们在此期间学到了很多东西,并且还了解了程序员处理大型项目时遵循的许多标准实践。 特别感谢导师Damian Vicino和Laouen Belloli。 他们不断地向我们提供有关我们工作的反馈,并教会了我们很多东西。
未来的工作 (Future Work)
After finishing all work that was necessary to make this library ready for review, we need to do some optimizations. This library always makes iterations from start for every calculation, this leads us to many repeated calculations. One can optimize this by storing the number at its last calculated precision. One more important optimization, also proposed by Laouen in his report, replace Tree Representation of the library to Directed Acyclic Graph(DAG).
完成使该库可供审查所需的所有工作之后,我们需要进行一些优化。 该库始终为每个计算从头开始进行迭代,这导致我们进行许多重复的计算。 可以通过以最后计算的精度存储数字来优化此精度。 劳恩(Laouen)在他的报告中还提出了另一项重要的优化方法,该方法将库的树表示替换为有向无环图(DAG)。
翻译自: https://medium.com/swlh/bringing-boost-real-to-review-ready-state-56b2582773d3
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








