从一元一次方程到伽罗瓦理论_多项式的根，和一般一元五次以上方程的不可解...

假设f是一个系数为整数的多项式。根据代数基本定理，复数是一个代数闭合域，也就是说所有系数为复数的多项式都在复数中有所有根。所以f当然在复数中有所有根。可以把f写作f=(x-α_1)……(x-α_n)，α_i为f的根。显然，如果对α_i进行置换，比如α_1→α_2，α_2→α_1，置换下的f肯定是不变的。

克罗内克以其“上帝创造了整数，其余都是人的工作”的信条出名。其中一个原因是以他命名的定理：如果F是一个域而f是多项式环F[x]中的一个非常数多项式，则存在扩域E/F使得对于E中某α我们有f(α)=0。

证明：假设p是f的一个不可约因式，我们只要找到这样一个E和α使得p(α)=0即可。因为p不可约，(p)这个理想在F[x]中是最大，所以F[x]/(p)是一个域。这就是我们要找的E。其中，可以定义α=x+(p)。那么，将α代入p这个多项式时，就有p(α)=p+(p)=0。

克罗内克以此认为所有数都由此而来。但我们知道存在超越数，即不是任何整数系数多项式的根的数，例如pi，e。实际上，代数数(即所有是整数系数多项式的根的数，即有理数的代数闭合)在复平面上只集中在一块很小的区域。复平面几乎全都不是代数数。

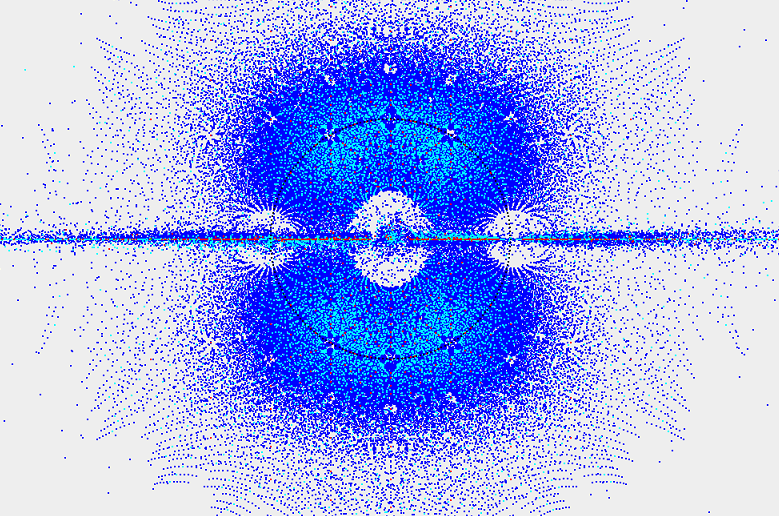
Algebraic numbers colored by degree (blue = 4, cyan = 3, red = 2, green = 1). The unit circle is black. (可以想一下为什么单位圆用黑色记)

Algebraic numbers on the complex plane colored by degree (re