三圆相交阴影部分面积_小学六年级图形面积的题很多家长都不会，一些初中生也未必会做...

大家好，这里是专注于小学和初中数学的数学世界，全部文章由数学老师猫哥原创，很高兴与大家一起分享和交流小学和初中数学的相关学习问题。今天给大家分享一道小学图形面积的计算题，这道题目看起来有点麻烦，很多同学瞬间觉得智商不够用了。这完全是一道小学数学题目，小学生完全可以做得出来。下面，我们看这道关于图形面积计算题的例子吧！

例题：如图，两个正方形的边长分别是3厘米和4厘米，CEG为扇形，连接AE、AG。求阴影部分的面积。

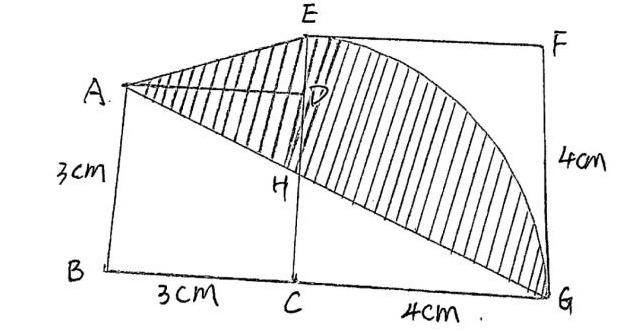
分析：由图可知，阴影部分是一个不规则图形，所以其面积就不能用所学的公式直接来求。我们观察发现，阴影部分的面积可以通过三部分图形面积相加减求出来，阴影部分=扇形面积+梯形面积-三角形面积，如此一来，即可解决问题。

解：梯形ABCE的面积为(3+4)×3÷2=10.5平方厘米

扇形面积为π×4×4÷4=4π平方厘米

三角形ABG的面积为(3+4)×3÷2=10.5平方厘米

所以，阴影部分的面积为4π+10.5-10.5=4π平方厘米

答：阴影部分的面积是4π平方厘米。

点评：解决本题的关键就是要弄清楚阴影部分的面积可以通过哪些图形的面积相加减求得，

到此为止，这道题就完整的解答出来啦！大家应该都可以看明白吧。如果不明白或者有更好的方法，欢迎大家与本人一起讨论。