已知两点坐标求水平距离_【一次函数】直线含参过定点，坐标含参寻定线

 本文大部分内容来自我八年级秋季课程第14讲(讲义获取方式见文末)，所以目标群体是八年级娃。当然，初三娃理应也能有所得。事实上，初三可进一步抬高视角，这是后话。

无锡八上期末试卷中的一次函数填选压轴题，以含参问题居多，这类问题，对一次函数解析式及图像的理解提出了更高的要求。而且，无锡中考也极喜欢考察含参二次函数，这正好是我本周要给九年级娃培训的课题。

事实上，一次函数y=kx+b(k≠0)中，比较有意思的就是k、b这两个参数，正是这两个参数在影响着函数解析式和图像。

对b的理解

在直线y=kx+b(k≠0)中，令x=0，则y=b，故直线过点(0，b)，换言之，b即直线与y轴交点的纵坐标。当b＞0时，直线与y轴交于正半轴；当b=0时，直线过原点；当b＜0时，直线与y轴交于负半轴。

对k的理解

一、k的正负

也就是说，k的正负决定了直线的倾斜方向，即向上倾斜还是向下倾斜(均指从左往右看)，教科书中对于k的论述，基本止步于此。

二、|k|的大小

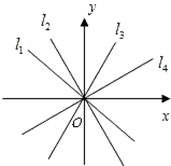
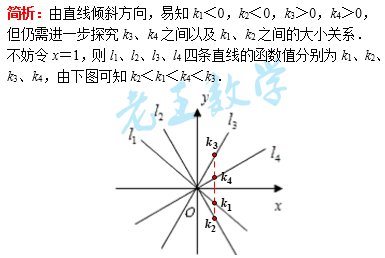
于是，我们发现：|k|的大小决定了直线的倾斜程度，|k|越大，直线越陡峭，越靠近y轴.

三、从数与形的双重角度，揭开k的神秘面纱

(一)从数的角度：

k即直线上任意两点纵坐标差与横坐标差的比值，可正可负。

(二)从形的角度：