函数最值问题的常用解法_一次函数中的最值问题的基本题型！

例一：直线L与x轴交与点A，与y轴交于B，已知直线L的解析式为y-x+4。D为OB中点，p是线段AB上一动点，求使OP+PD值最小的点P的坐标。

例二：已知点A(1，5)，B(3，-1)，点M在x轴上，当AM-BM最大时，求M的坐标。

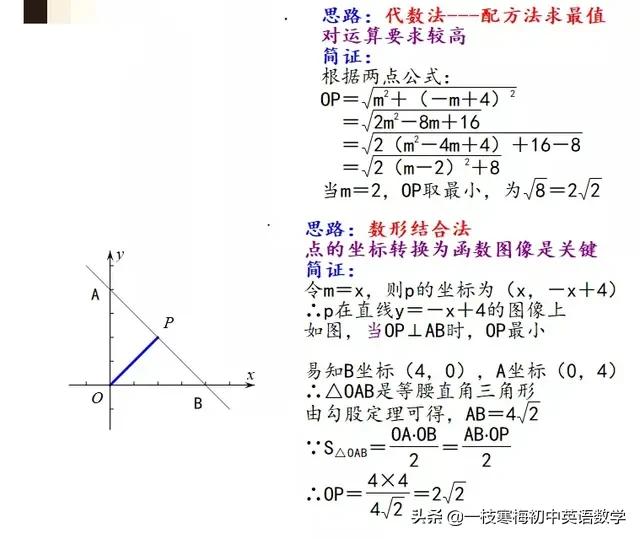
例三：在平面直角坐标系中，点P的坐标为(m，-m+4)，则点P到原点的最短距离是________.

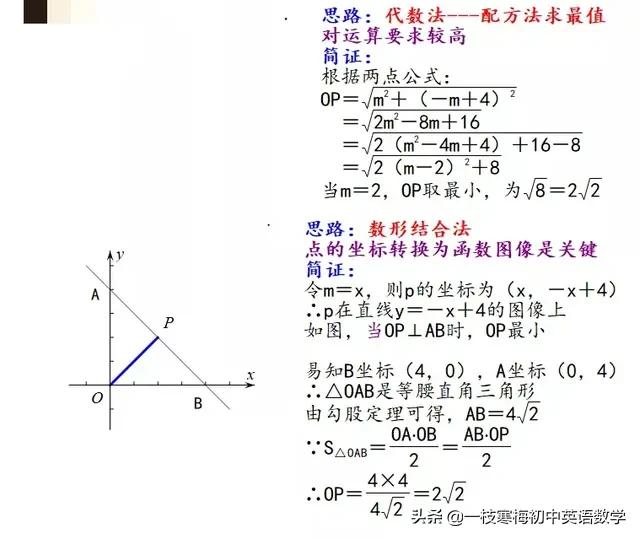
例四：已知实数a，b满足2a+b=2，则在平面直角坐标系中，求动点p(a，b)到坐标原点O距离的最小值。

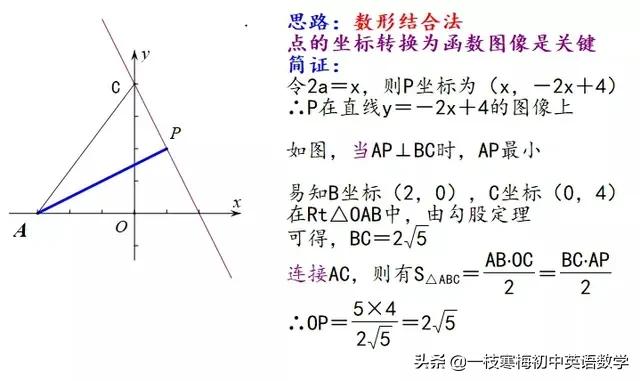
例五：无论a取什么实数，动点P(2a，-4a+4)总在直线L上运动，点A的坐标为(-3，0)，求线段AP的最小值。

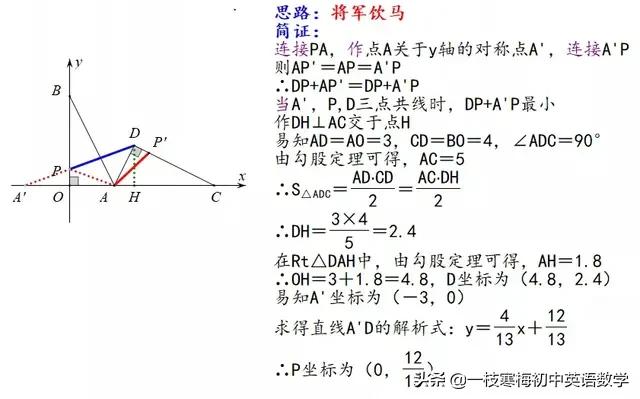
例六：在平面直角坐标系中，已知O为坐标原点，点A(3，0)，B(0，4)，以点A为旋转中心，把△ABO顺时针旋转到△ACD，C恰好落在x轴正半轴上。已知边OB上的一点P旋转后的对应点为P′，当DP+AP′取得最小值是，求P的坐标。

综上，我们解决一次函数最值问题常用解法包括：“将军饮马”，数形结合法，配方法求最值，三角形的三边关系等方法。

声明：来源于网络，如有侵权请联系删除！