神经网络的数学基础：张量和梯度

最新推荐文章于 2022-11-29 17:12:07 发布

科技与文明

最新推荐文章于 2022-11-29 17:12:07 发布

阅读量8k

点赞数 25

分类专栏：机器学习系列文章标签：机器学习深度学习梯度神经网络张量

本文链接：https://blog.csdn.net/weixin_28710515/article/details/89228892

版权

机器学习系列专栏收录该内容

13 篇文章 12 订阅

订阅专栏

阅读上一篇深度学习的“Hello World”
今天主要讲神经网络的数学基础，涉及的数学包括线性代数、矩阵分析、微积分和数理统计等科目。主要讲清楚两个概念张量和梯度，这两个概念对于了解和掌握机器学习(深度学习)尤为重要，在介绍这两个概念之前，我们来了解一下Google的神经网络游乐园。

开篇

Google是人工智能的领导者，在人工智能方面的建树，无需赘述了。Google官方有一个神经网站游乐园，可以让你形象直观的观察神经网络训练的过程，包括训练结果的变化，你可以修改神经网络的层数，以及相关的参数，再运行，看起来很直观，如果你感兴趣，还可以到Google官方的Github上下载该项目在本地运行,以下是从运行中截取的一张图：
图1-1

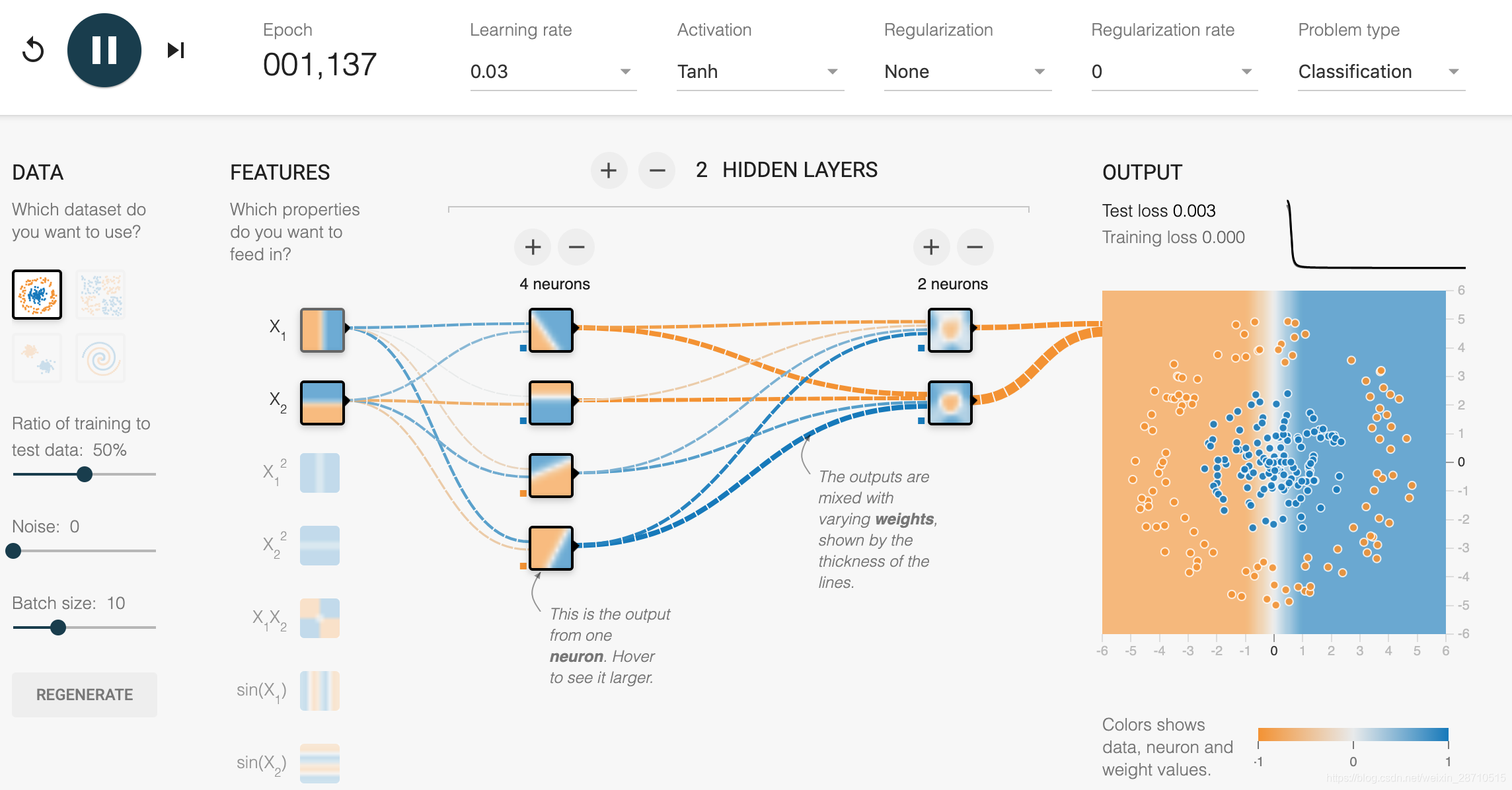
你可以直观的看到数据在网络中流动的情形，Google的机器学习框架叫做 TensorFlow，这是个很形象的比喻，意思是 张量(Tensor)在神经网络中流动(Flow)，可以看出张量是多么重要！张量对这个领域非常重要，重要到Google 的TensorFlow 都以它来命名。下面我们就来谈谈张量。

张量

神经网络使用的数据存储在多维Numpy 数组中，也叫张量（tensor），所以张量其实就是多维数组，所以不能叫做矩阵，矩阵只是二维的数组，张量所指的维度是没有限制的。一般来说，当前所有机器学习系统都使用张量作为基本数据结构。那么什么是张量？张量这一概念的核心在于，它是一个数据容器。它包含的数据几乎总是数值数据，因此它是数字的容器。你可能对矩阵很熟悉，它是二维张量。张量是矩阵向任意维度的扩展。下面对0到3维张做一些描述和实验，以加深理解。

注意，张量的维度（dimension）通常叫作轴（axis）

1、标量(scalar)

仅包含一个数字的张量叫作标量（scalar，也叫标量张量、零维张量、0D 张量）。在Numpy中，一个float32 或float64 的数字就是一个标量张量（或标量数组）。你可以用ndim 属性来查看一个Numpy 张量的轴的个数。标量张量有0 个轴（ndim=0）。张量轴的个数也叫作阶（rank）。

2、向量(vector)

数字组成的数组叫作向量（vector）或一维张量（1D张量）。一维张量只有一个轴。

3、矩阵(matrix)

向量组成的数组叫作矩阵（matrix）或二维张量（2D 张量）。矩阵有2个轴（通常叫作行和列）。你可以将矩阵直观地理解为数字组成的矩形网格。

4、3D张量与更高维张量

将多个矩阵组合成一个新的数组，可以得到一个3D 张量，你可以将其直观地理解为数字组成的立方体。将多个3D 张量组合成一个数组，可以创建一个4D 张量，以此类推。深度学习处理的一般是0D 到4D 的张量，但处理视频数据时可能会遇到5D 张量。

张量的关键属性

张量是由以下三个关键属性来定义的:

轴的个数（阶）。例如，3D 张量有3个轴，矩阵有2个轴。这在 Numpy 等 Python 库中也叫张量的ndim。
形状(shape)。这是一个整数元组，表示张量沿每个轴的维度大小（元素个数）。例如，前面矩阵示例的形状为(3, 5)，3D 张量示例的形状为(3, 3, 5)。向量的形状只包含一个元素，比如(5,)，而标量的形状为空，即()。
数据类型（在 Python 库中通常叫作 dtype）。这是张量中所包含数据的类型，例如，张量的类型可以是float32、uint8、float64 等。在极少数情况下，你可能会遇到字符（char）张量。注意，Numpy（以及大多数其他库）中不存在字符串张量，因为张量存储在预先分配的连续内存段中，而字符串的长度是可变的，无法用这种方式存储。

练习

把一个数不断的加[]让它变成多维数组，以及演示如何取数组的元素。

>>> data = np.array(12)
>>> print(data.ndim, data.shape,data)
0 () 12
>>> data = np.array([data])
>>> print(data.ndim, data.shape,data)
1 (1,) [12]
>>> data = np.array([data,[13]])
>>> print(data.ndim, data.shape,data)
2 (2, 1) [[12][13]]
>>> data = np.array([data,data,data])
>>> print(data.ndim, data.shape,data)
3 (3, 2, 1) [[[12][13]][[12][13]][[12][13]]]
>>> data.ndim, data.shape,data
(3, (3, 2, 1), array([[[12],[13]],[[12],[13]],[[12],[13]]]))
>>> data[0]
array([[12],[13]])
>>> data[1]
array([[12],[13]])
>>> data[2]
array([[12],[13]])
>>> data[0][1][1]
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
IndexError: index 1 is out of bounds for axis 0 with size 1
>>> data[0][1][0]
13

梯度

为了很好的理解梯度，我们先来回顾一下导数，偏导数的定义

导数

在高等数学中学过导数，导数就是表示某个瞬间的变化量，它可以定义成下面的式子：

$\frac{df(x)}{dx}=\lim_{x \to 0}\frac{f(x+h)-f(x)}{h}$

利用微小的差分求导数的过程称为数值微分(numerical differentiation)。

偏导数

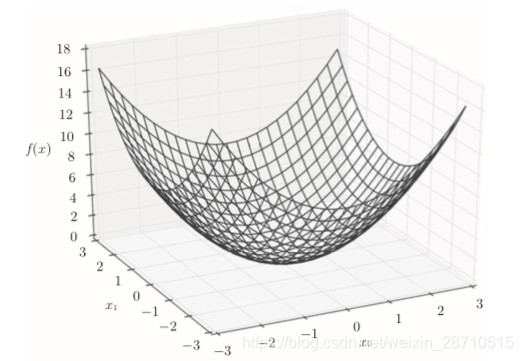
有多个变量的函数的导数称为偏导数，比如一个有两个变量的函数：

$f(x0,x1) = x0^2 + x1^2$

在某一个具体的点（3，4），就有两个导数，用数学表达式表示如下： $\frac {\theta f}{\theta x0},\frac {\theta f}{\theta x1}$
该函数图像如下：
图1-2

梯度

由全部变量的偏导数汇总而成的张量称为梯度(gradient)
我们按变量分别计算了x0 和 x1的偏导数。现在，我们希望一起计算x0和x1的偏导数。比如，我们来考虑求x0 =3,x1 =4时的偏导数： $(\frac {\theta f}{\theta x0},\frac {\theta f}{\theta x1})$
这样由所有变量的偏导数汇总而成的向量成为梯度。可以看出梯度实质是一个张量，内容是所有变量在某点的偏导数的集合，只不过使用张量一次性方便描述和计算。

练习

为量巩固对导数、偏导数、梯度的理解和认识，练习时最好的方式，以下是练习的全部代码，根据需要打开 Test Case部分的注释，代码已经自带解释了。

# coding: utf-8
import matplotlib.pylab as plt
import numpy as np

class Diff2Gradient(object):
    def numerical_diff(self, f, x):
        """
        函数求导数,实例是求1个自变量的函数
        :param f: 传递的参数可以是一个函数
        :param x: x 可以是多维数组，代表多个点
        :return: 返回x中点的导数，值是跟x.shape相同的数组
        """
        h = 1e-4  # 0.0001
        return (f(x + h) - f(x - h)) / (2 * h)

    def numerical_gradient(self, f, X):
        """
        求导数
        :param f:
        :param X: 可以是多维数组
        :return: 返回X.shape的导数值
        """
        if X.ndim == 1:
            return self._numerical_gradient_no_batch(f, X)
        else:
            grad = np.zeros_like(X)

            # 维度上循环
            for idx, x in enumerate(X):
                # print('{}->{}'.format(idx, x))
                grad[idx] = self._numerical_gradient_no_batch(f, x)

            return grad

    def _numerical_gradient_no_batch(self, f, x):
        """
        返回一行的导数值
        :param f: 一个自变量函数
        :param x: x 可以是一维数组
        :return:
        """
        h = 1e-4  # 0.0001
        grad = np.zeros_like(x)

        for idx in range(x.size):
            tmp_val = x[idx]
            x[idx] = float(tmp_val) + h
            # 这是把整个x变量带入函数，x里只有x[idx]值变了
            fxh1 = f(x)  # f(x+h)

            x[idx] = tmp_val - h
            fxh2 = f(x)  # f(x-h)
            grad[idx] = (fxh1 - fxh2) / (2 * h)

            x[idx] = tmp_val

        return grad

    def tangent_line(self, f, x):
        """
        求切线函数
        :param f: 原来函数
        :param x: 选的x点
        :return: 一个函数(形式 kx+b)
        """
        d = self.numerical_diff(f, x)
        y = f(x) - d * x

        return lambda t: d * t + y


def function_1(x):
    return 0.01 * x ** 2 + 0.1 * x

def function_2(x):
    if x.ndim == 1:
        return np.sum(x ** 2)
    else:
        return np.sum(x ** 2, axis=1)

if __name__ == '__main__':
    d2g = Diff2Gradient()

    # # Test Case 1: 自变量只有一个的情况
    # # 传入参数说明，传入1个值，返回一个值的导数，传入数组就返回数值中
    # # 每个值处的导数，这是Numpy看起来有点神奇的地方。
    # print(d2g.numerical_diff(function_1, 2.5))
    # print(d2g.numerical_diff(function_1, np.array([2.5])))
    # print(d2g.numerical_diff(function_1, np.array([2.5, 4, 5])))
    # print(d2g.numerical_diff(function_1, np.array([[2.5, 3, 5, 6], [12, 2.5, 4, 3]])))
    #
    # x = np.arange(0.0, 20.0, 0.1)
    # y = function_1(x)
    # plt.xlabel("x")
    # plt.ylabel("f(x)")
    #
    # tf = d2g.tangent_line(function_1, 5)
    # y2 = tf(x)
    #
    # # 绘制f(x)函数和切线，这里要理解函数可以作为
    # # 参数传递的技巧，再一次展现Python作为动态语
    # # 言的一个优势。
    # plt.plot(x, y)
    # plt.plot(x, y2)
    # plt.show()

    # Test Case 2:
    x0 = np.arange(-2, 2.5, 1)
    x1 = np.arange(-1, 3.5, 1)
    # 返回两个数组组成的数组，一个数组[x1.size * x0.size].
    # 每行是x0所有数值；第二个数组是[x1.size * x0.size],
    # 每1行的值是x1[0]第2行值是x1[1],以此类推。
    X, Y = np.meshgrid(x0, x1)
    X = X.flatten()
    Y = Y.flatten()
    points = np.array([X, Y])
    grad = d2g.numerical_gradient(function_2, points)

    c = np.random.randn(len(X))  # arrow颜色

    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1], c, angles="xy")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.legend()
    plt.draw()
    plt.show()

继续下一篇阅读神经网络的数学基础：张量运算

科技与文明

关注

25
点赞
踩
62

收藏

觉得还不错? 一键收藏
打赏
0
评论
神经网络的数学基础：张量和梯度

阅读上一篇深度学习的“Hello World” 今天主要讲神经网络的数学基础，涉及的数学包括线性代数、矩阵分析、微积分和数理统计等科目。主要讲清楚两个概念张量和梯度，这两个概念对于了解和掌握机器学习(深度学习)尤为重要，在介绍这两个概念之前，我们来了解一下Google的神经网络游乐园。开篇Google是人工智能的领导者，在人工智能方面的建树，无需赘述了。Google官方有一个神经网站游乐园...
复制链接

扫一扫