同底数幂比较大小方法_三个视频搞定：指数函数单调性比较大小、解不等式与方程、求类指数函数值域...

● 本文适合高一上学期、高三一轮复习的同学阅读。先看视频再看文字，看视频时注意利用暂停，想清楚每一步变形的依据。

01

利用指数函数单调性比较大小

视频讲解

1、不同底指数函数图象的相对位置

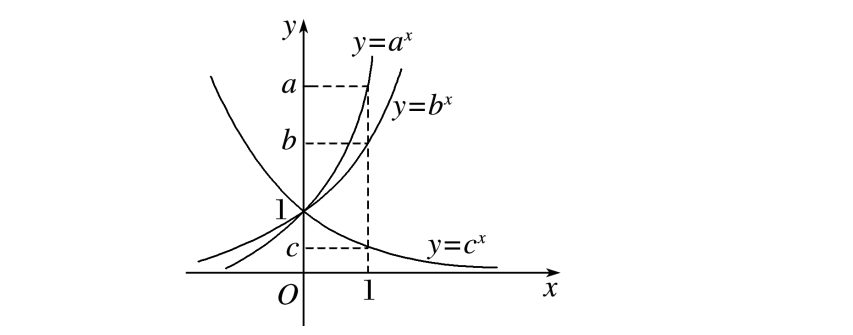
在同一坐标系中有多个指数函数图象时，图象的相对位置与底数大小有如下关系：

(1)在y轴右侧，图象从上到下相应的底数由大变

小；在y轴左侧，图象从下到上相应的底数由大

变小.即无论在y轴的左侧还是右侧，底数按逆时针方向变大.这一性质可通过令x＝1时，y＝a去理解，如图.

(2)指数函数y＝a^x与y＝(1/a)^x (a＞0且a≠1)的图象关于y轴对称。

2、比较幂的大小

(1)对于同底数不同指数的两个幂的大小，利用指数函数的单调性来判断；

(2)对于底数不同指数相同的两个幂的大小，利用指数函数的图像的变化规律来判断；

(3)对于底数不同指数也不同的两个幂的大小，则通过中间值 来判断。

3、比较大小举例

02

利用指数函数单调性解方程、不等式

视频讲解

解指数方程

解指数不等式

小结：

解指数方程、不等式的基本方法是先化为同底指数式，再利用指数函数单调性化为常规的方程、不等式来解，注意底数对不等号方向的影响。

03

类指数函数定义域、值域

视频讲解

小结：

解此类题的要点是设a^x＝t，利用指数函数的性质求出t的范围.从而把问题转化为y＝f(t)的问题。

小结：

y＝a^f(x)的定义域即f(x)的定义域，求y＝a^f(x)的值域可先求f(x)的值域，再利用y＝a^t的单调性结合t＝f(x)的范围求y＝a^t的范围。

1、三个视频搞定：指数函数概念、指数函数图像及图像关系的识别、指数函数图像过定点问题

2、三个视频搞定：根式性质、根式与指数式互化、有理数指数幂性质扩展至实数指数幂

(本文部分图片与视频来自于网络，仅供学习交流用，若有不妥，请联系删除。)

人生有缘才相遇 扫码相识更有趣

微信号 :rong19711107 

公众号：周老师松果数学

● 扫码联系我

zlssgsx