同底数幂比较大小方法_指对幂比较大小的那些事

点击蓝字｜关注我们

指数对数幂函数大小比较

欢迎来到众学小课堂！由于最近高一的小朋友们正在学习指数对数幂函数这一部分内容，再加上有不少小朋友私下和我吐槽这类比较大小的题目非常“打脑壳”。于是！小李老师终于忍受不了重复讲授n次的痛苦，选择将这类比较大小的题目汇总整理并且附上独家秘笈做成一篇小推文。

基础回顾

首先，让我们先来整体复习一下指对幂函数的基本知识！

指数

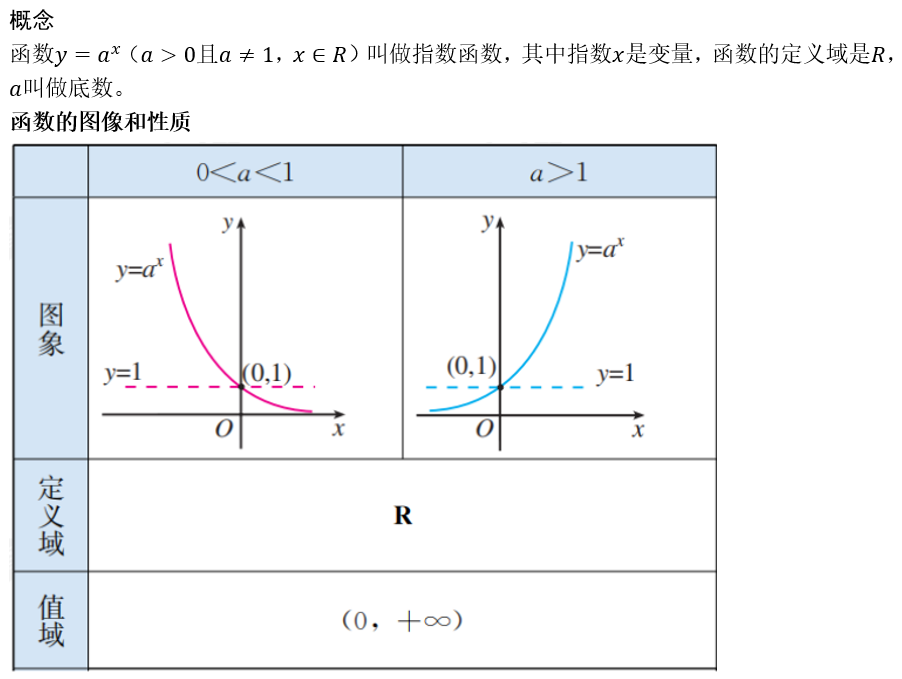
对数

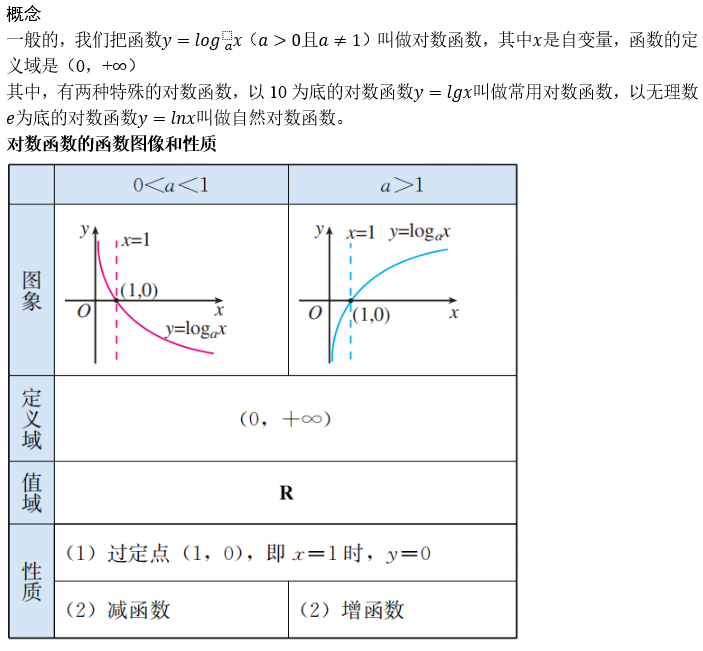
幂函数

比较方法

两种比较大小的方法

在复习完前面的基础知识后，就要进入到本文的重点：指数，对数，幂函数大小比较的常用方法。这一部分题目相信正在深深地折磨了很多小朋友，那么今天，小李老师就为大家讲解一下，解决比较大小问题的两个法宝——媒介法和转化法！

媒介法

首先是媒介法，媒介值主要适用于两类题目。

第一类题目是比较多个底数，指数(真数)都不相同的函数

第二类题目是一道题目同时出现底数，指数，幂函数进行比较大小

一般媒介法有两种情况，第一是以0，1作为划分界限，将函数先与0，1进行比较，再利用单调性求解。第二是选择一个或多个函数，以它为媒介对题目中的函数进行研究，一般也要利用函数的单调性。

经典例题

左右滑动查看答案

转化法

第二种常用的方法就是转化法，主要思路就是把不同底数，指数(真数)的函数，转化为同一个底数，指数(真数)的函数。

经典例题

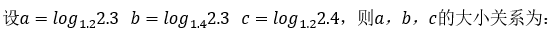
规律总结

解题套路

其实，指数对数幂函数比较大小并不复杂，解题思路大致是：先粗略判断各项与0，1的关系，接下来可以选取媒介函数利用单调性比较大小，或者转化为同底数，同指数(真数)的函数再利用单调性比较大小。

变式练习

最后的最后，再给大家布置一个小练习，答案和解析会公布在下一篇推文哦！

扫码关注我们

微信号｜zhongxue_education