Neuman边界条件

Neuman边界条件

对这样一个问题

我的目标：

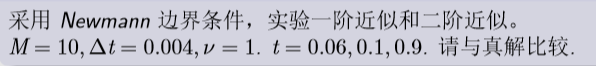
我们有如下的效果：

一阶近似

1. t=0.06
   

2. t = 0.1
   

3. t = 0.9
   

二阶近似

1.t=0.6

2.t=0.1

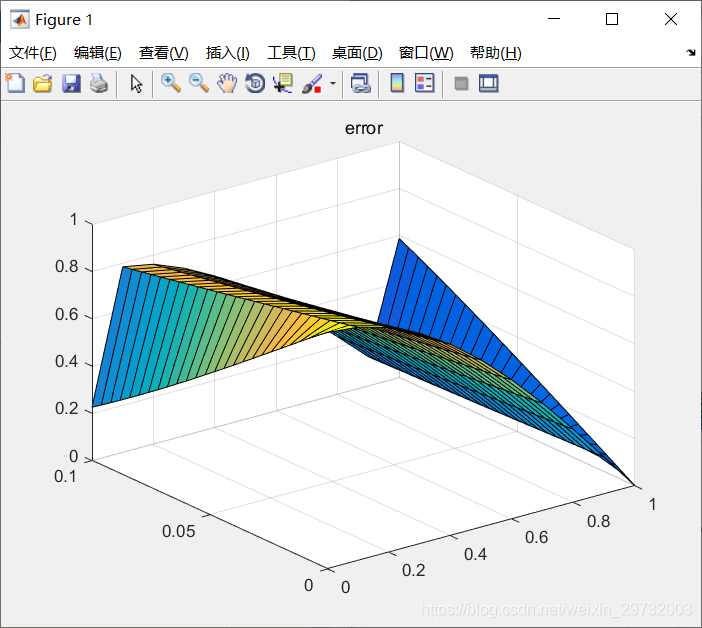
3.t = 0.9

误差的差别

改变步长

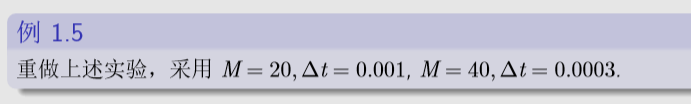
取t=0.9
1.M=20,dt = 0.001

一阶

二阶

差别

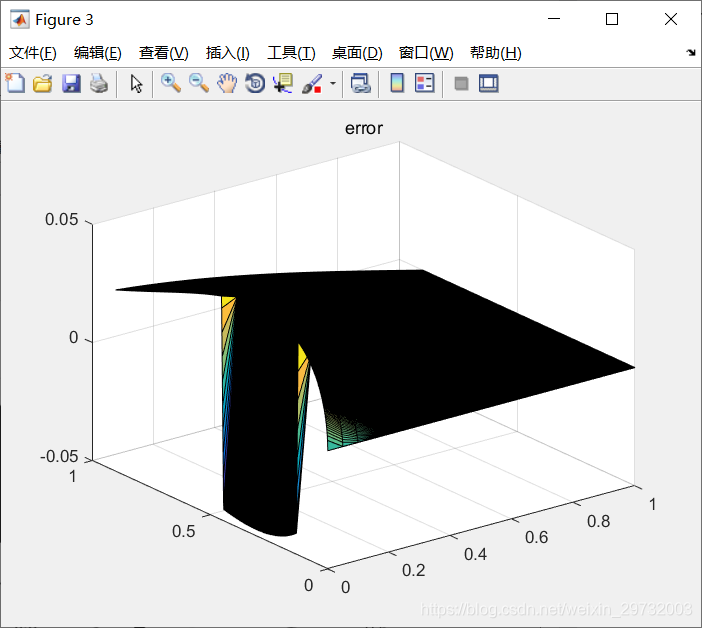
2.M=40,dt=0.0003，t=0.6

第二道题

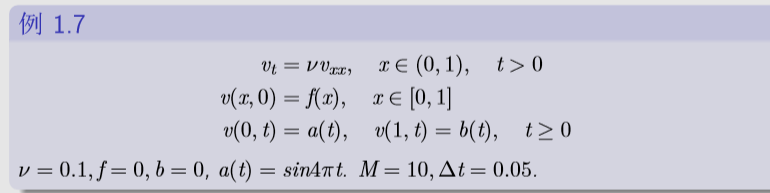
t = 0.9


描述了物体受到的热量扩散的情况，一定空间内，距离热源比较远的地方，随着时间的增长，该处也会发生热交换的现象

全部代码如下：

clear; clc; close all;
%% 例1.4
%% 一阶近似
m = 40; dt=0.0003;t = 0.06;a=1;dx = 1/m;n = t/dt;
u = zeros(n+1,m+1);
v = zeros(n+1,m+1);% 真解
x = zeros(1,m+1);
%一阶近似 u(0,t)=u(dx,t),u(x,0)=cos(pi*x/(2*180))
for i = 1:m
    x(i) = (i-1)*dx;
    u(1,i) = cos(pi*x(i)/2);
end
for j = 1:n
     for i = 2:m%u(1,t)=0导致的
         u(j+1,i) = u(j,i) + a*(dt/dx^2)*(u(j,i+1)-2*u(j,i)+u(j,i-1));
     end
     u(j+1,1) = u(j+1,2);%这是由一阶近似dux(0,t)=0决定的
end
%真解
f = @(x,t)(exp(-4*((pi)^2)*(a^2)*t)*sin(2*pi*x));
n = t/dt;
T = zeros(1,n+1);
for j = 1:n+1
    T(j) = (j-1)*dt;
end
for j = 1:n+1
     for i = 1:m+1
         v(j,i) = f(T(j),x(i));
     end
end
error1 = abs(u-v);
%draw
vecx = 0:dx:1;
vect = 0:dt:t;
[xx,tt] = meshgrid(vecx,vect);
figure(1)
surf(xx,tt,error1)
title('error')
%% 二阶近似
m = 40; dt=0.0003;t = 0.06;a=1;dx = 1/m;n = t/dt;
u = zeros(n+1,m+1);
v = zeros(n+1,m+1);% 真解
x = zeros(1,m+1);
%一阶近似 u(0,t)=u(dx,t),u(x,0)=cos(pi*x/(2*180))
for i = 1:m
    x(i) = (i-1)*dx;
    u(1,i) = cos(pi*x(i)/2);
end
for j = 1:n
     for i = 2:m%u(1,t)=0导致的
         u(j+1,i) = u(j,i) + a*(dt/dx^2)*(u(j,i+1)-2*u(j,i)+u(j,i-1));
     end
     u(j+1,1) = u(j,1)+a*(dt/dx^2)*(u(j,2)-u(j,1));%二阶近似
end
%真解
f = @(x,t)(exp(-4*((pi)^2)*(a^2)*t)*sin(2*pi*x));
n = t/dt;
T = zeros(1,n+1);
for j = 1:n+1
    T(j) = (j-1)*dt;
end
for j = 1:n+1
     for i = 1:m+1
         v(j,i) = f(T(j),x(i));
     end
end
error2 = abs(u-v);
%draw
vecx = 0:dx:1;
vect = 0:dt:t;
[xx,tt] = meshgrid(vecx,vect);
figure(2)
surf(xx,tt,error2)
title('error')
%% difference
figure(3)
surf(xx,tt,error2-error1)
title('error')

%% 例1.4
%% 
m = 10; dt=0.05;t = 0.9;a=1;dx = 1/m;n = t/dt;
u = zeros(n+1,m+1);
u(1,:) = 0;%f=0
u(:,m+1) = 0;%u(0,t)=0
T = 0:dt:t;
at = sin(4*pi*T);
u(:,1) = at;
for j = 1:n
     for i = 2:m%u(1,t)=0导致的
         u(j+1,i) = u(j,i) + a*(dt/dx^2)*(u(j,i+1)-2*u(j,i)+u(j,i-1));
     end
end
%draw
vecx = 0:dx:1;
vect = 0:dt:t;
[xx,tt] = meshgrid(vecx,vect);
figure(1)
surf(xx,tt,u)
title('re')
xlabel('space') 
ylabel('time')