【常用算法总结——逆元】

乘法逆元，一般是用来求

的值，p通常为质数

定义

若a*x≡1(mod b),且a与b互质，我们定义x是a的逆元，记为a^(-1)，所以也可以说x是a在mod b意义下的倒数

所以对于a/b(mod p)，我们可以先求出b在mod p下的逆元，然后乘a再mod p就是这个分数的值了

逆元求法

　　首先看到同余方程，这个就是典型的求一个数模p下的逆元，而对于逆元的求法，我们有多种操作：

扩展欧几里得

　　首先，这个算法的性质如下

扩展欧几里德算法是用来在已知a, b求解一组x，y，使它们满足贝祖等式： ax+by = gcd(a, b) =d（解一定存在，根据数论中的相关定理）。扩展欧几里德常用在求解模线性方程及方程组中。

　　在这道题中，我们可以把ax≡1(mod b)转化成ax+by=1，只不过y可能是负数，然而与扩欧公式还是有差别，但不难得出，gcd(a,b)=1,

　　推导公式如下

由最大公因数的定义，可知 a 是 gcd(a,b) 的倍数，且 b 是 gcd(a,b) 的倍数，
若 x,y 都是整数，就确定了 ax + by 是 gcd(a,b) 的倍数，
因为 m = ax + by所以 m 必须是 gcd(a,b) 的倍数，
那么 m \mod gcd(a,b) = 0

..................................................

然后根据一系列推导就得出了具体公式：具体请见同余方程第一篇题解<<<<大佬。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 long long x,y;
 4 void exgcd(long long a,long long b)
 5 {
 6     if(b==0)
 7     {
 8         x=1;
 9         y=0;
10         return;
11     }
12     exgcd(b,a%b);
13     long long z=x;
14     x=y;
15     y=z-(a/b)*y;
16 }
17 int main()
18 {
19     long long a,b;
20     cin>>a>>b;
21     exgcd(a,b);
22     while(x<0)
23         x+=b; 
24     x%=b;
25     cout<<x;
26     return 0;
27 }

快速幂

　　这个做法运用到了费马小定理

若p为素数，a为正整数，且a、p互质。 则有a^(p-1)≡1(mod p)。

然后代入原式，神奇的事发生了

a*x≡1(mod p)
a*x=a^(p-1) (mod p)
x=a^(p-2) (mod p)

然后我们求a^(p-2)(mod p)就是它的逆元啦

 1 #include<bits/stdc++.h>
 2 #define ll long long
 3 using namespace std;
 4 ll n,p;
 5 int fpm(ll x,ll y)//快速幂
 6 {
 7     x%=p;
 8     ll ans=1;
 9     while(y)
10     {
11         if(y&1)ans=(ans*x)%p;
12         y>>=1;
13         x=x*x%p;
14     }
15     return ans;
16 }
17 int main()
18 {
19     cin>>n>>p;
20     for(int i=1;i<=n;i++)
21     {
22         printf("%lld\n",fpm(i,p-2));
23     }
24 }

 线性算法

　　以上算法针对于求单个逆元，但是有一长串的时候，你就TLE了，所以，聪明的大佬们研发的线性算法出现了。

　　设x的逆元为x^(-1)

　　我们先有一个1的逆元为1

       设p=k*i+r,(1<r<i<p) 也就是 k 是 p / i的商，r是余数 。

　　

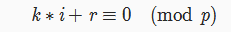
然后乘上i的逆元和r的逆元

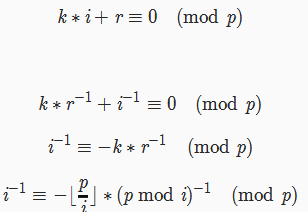
然后公式就出来了

 1 #include<bits/stdc++.h>
 2 #define ll long long
 3 using namespace std;
 4 ll n,p;
 5 ll inv[3000005];
 6 int main()
 7 {
 8     cin>>n>>p;
 9     inv[1]=1;
10     printf("%lld\n",inv[1]);
11     for(int i=2;i<=n;i++)
12     {
13         inv[i]=(p-p/i)*inv[p%i]%p;
14         printf("%lld\n",inv[i]);
15     }
16 }

 

学会了求逆元后，我们就可以学学其他interesting的东西——中国剩余定理

 

转载于:https://www.cnblogs.com/hualian/p/11240742.html