【机器学习具体解释】KNN分类的概念、误差率及其问题

转载请注明出处：http://blog.csdn.net/luoshixian099/article/details/50923056

勿在浮沙筑高台

KNN概念  

      KNN(K-Nearest Neighbors algorithm)是一种非參数模型算法。在训练数据量为N的样本点中，寻找近期邻測试数据x的K个样本，然后统计这K个样本的分别输入各个类别w_i下的数目k_i，选择最大的k_i所属的类别w_i作为測试数据x的返回值。当K=1时，称为近期邻算法，即在样本数据D中，寻找近期邻x的样本，把x归为此样本类别下。经常使用距离度量为欧式距离。

算法流程：

                 

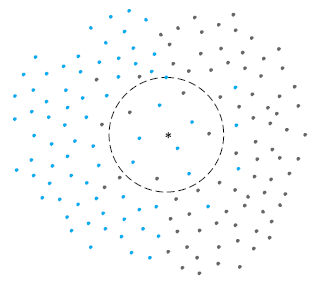
左图所看到的：在二维平面上要预測中间'*'所属颜色，採用K=11时的情况，当中有4黑色，7个蓝色，即预測'*'为蓝色。

右图所看到的：当K=1时，即近期邻算法。相当于把空间划分成N个区域，每一个样本确定一块区域。每一个区域中的点都归属于该样本的类别，由于该区域的数据点与所用样本相比与区域样本近期，此算法也被称为Voronoi tessellation。

--------------------------------------------------------------------------------------------------------------------------------------------

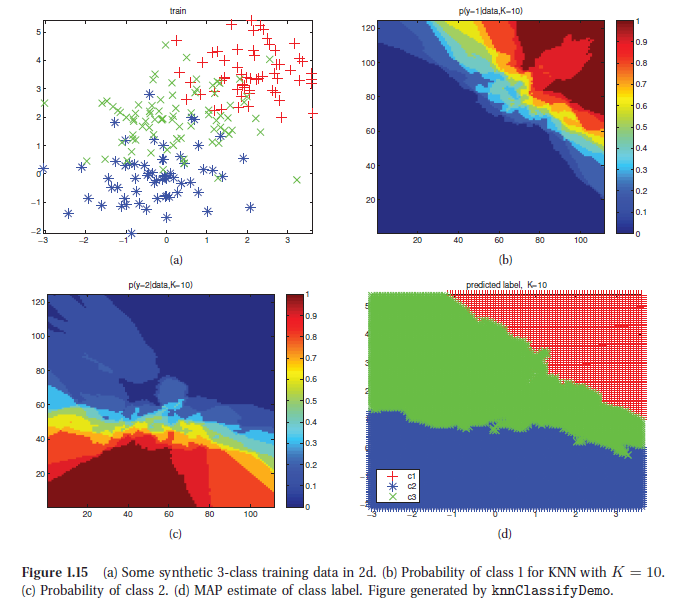
  以下四副图像是在一个二维平面上。数据点类别为3类。採用K=10。图(a)为样本数据点。图(b)为平面上每一个位置属于y=1(相应‘+’)的概率热量图像。图(c)为类别y=2(相应'*')时相应的热量图像；图(d)採用MAP预计（即最大概率的类别）平面各点所属类别。

  

------------------------------------------------------------------------------------------------------------------

KNN算法误差率

如果最优贝叶斯分类率记为P_B,依据相关论文证明KNN算法的误差率为：

当数据样本量N趋于无穷大时。K=1时：    ，M为数据类别总数

当数据样本量N趋于无穷大时，M=2时:;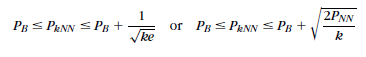

由公式看出，KNN的算法要优于1-NN算法，由于减少了误差下界。

并随着k的增大。P_kNN渐近于最优误差率P_B；其实，当k->∞时(但仍然占样本总量N非常小一部分)，KNN算法准确率趋近于贝叶斯分类器。

KNN算法的问题

• 当数据量N非常大，同一时候数据维度D非常高，搜索效率会急剧下降。

  若採用暴力求解法。复杂度为

  。为增大效率，能够採用KD树等算法优化。见：KD树与BBF算法解析
• 有时依据现实情况，须要减少样本数量，能够採用prototype editing或者condensing算法等；prototype editing算法採用自身数据样本作为測试样本，应用KNN算法，若分类错误则剔除该样本。
• 当样本总量N非常小时，会造成错误率上升。一种解决的方法是训练度量距离方法，对不同的样本採用不同的度量方法目的是为了减少错误率。此种方法能够分为：全局方法(global)、类内方法(class-dependent)、局部方法(locally-dependent)。

Ref：Machine Learning: A Probabilistic Perspective

         Pattern Recognition,4th.

转载于:https://www.cnblogs.com/wzzkaifa/p/7281622.html