关于矩阵的秩的重要结论

今天要讲的是关于矩阵秩的重要结论。关于矩阵的秩，讲三点，前两点是比较重要的，专门提出来强调一下，第三点是书上没有的一个重要的结论：

1、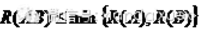，也就是一个矩阵与另一个矩阵相乘后，新矩阵的秩一定不大于原矩阵。怎么证明呢，结合线性结合线性方程组的有解性来进行证明的，AB=C，已经说明了AX=C是有解的，而线性方程组的有解性与矩阵的秩的关系说明了R（A）=R（A，C），所以A的秩大于等于C的秩，再将此矩阵两边转置，再根据线性方程组的解与矩阵的秩间关系同理可得A的秩大于等于C的秩.当我们学习了与线性表示有关的系统性理论后对这个定理会有更直观的理解。

2、矩阵左乘列满秩矩阵后新矩阵的秩与原矩阵的秩一样，此结论希望引起大家重视，此结论就是同济大学第五版70页的例9，大家可以参照此过程。

3、给出一个关于矩阵的秩的一般性的结论，

大家记住了的话对做题有很大的帮助，证明过程复杂，不要求掌握。

今天看一道考研的选择题：

上述是脱离了方程组单独讲的矩阵的秩的结论，而当秩与方程组结合时也有重要结论，对于方程组Ax=b

1、如果A是行满秩的矩阵，那么方程组要么有唯一解，要么有无穷多解。

如果A是行满秩的矩阵，因为矩阵的列秩等于矩阵的行秩，所以矩阵的列秩等于矩阵的行数，所以矩阵的列向量的线性组合一定能得到所有该维数的列向量。怎么理解呢？比如A是2x4的矩阵，A的秩为2，那么组成A的四个列向量的秩为2，这四个列向量都是2维的，那这四个列向量是不是能线性组合成任意的二维列向量，所以一定有解。

A的形式要么是矮且胖要么是方阵（矩阵的列不可能小于矩阵的行数），如果矩阵A矮且胖的话，那么对线性方程组的约束的个数（矩阵的行数）小于未知数的个数，那就是无穷多解。矩阵A是方阵，根据克拉默法则我们也能得出是唯一解。

上面是我们根据我们对线性代数的直观理解做出的推导，那么这个结论怎么证明呢？

2、如果A是列满秩的话，那么方程组要么有唯一解，要么无解。

       两个结论看起来类似，但直观理解的角度不太一样。A要么是方阵，要么是瘦高型，A是方阵时根据克拉默法则也可知有唯一解，A是瘦高型的话，A的线性组合如果能构成b就是唯一解，不能构成b就无解了。（因为A中各列线性无关，最后x不可能有无穷多解）

     还有一个角度，b是A中各列线性组合，b的这一列加到A后如果矩阵的秩加了1，说明无解，如果矩阵的秩不变，说明有唯一解。

转载于:https://www.cnblogs.com/rainbow70626/p/8886858.html